中考数学试题分类汇编514精选.doc

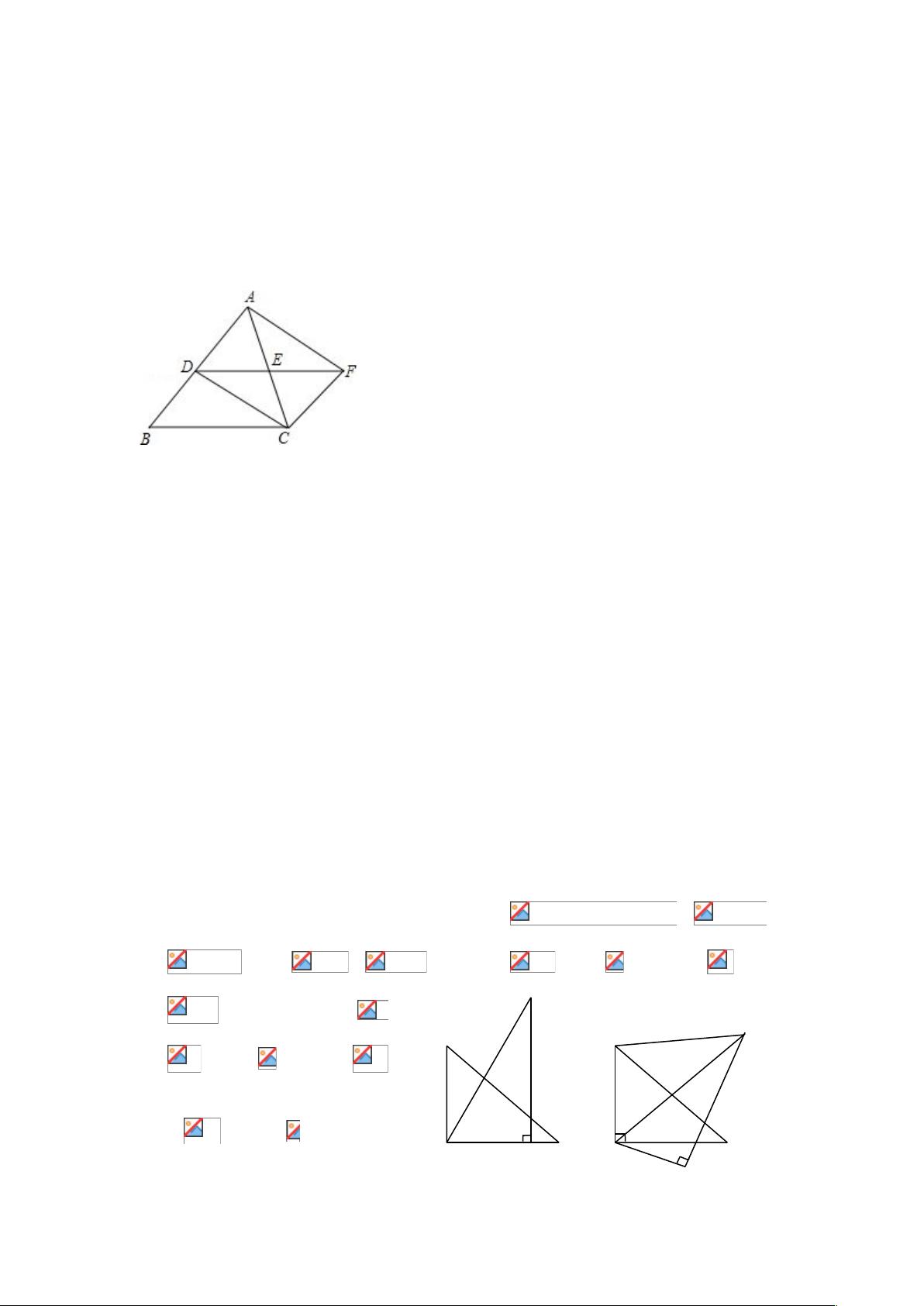
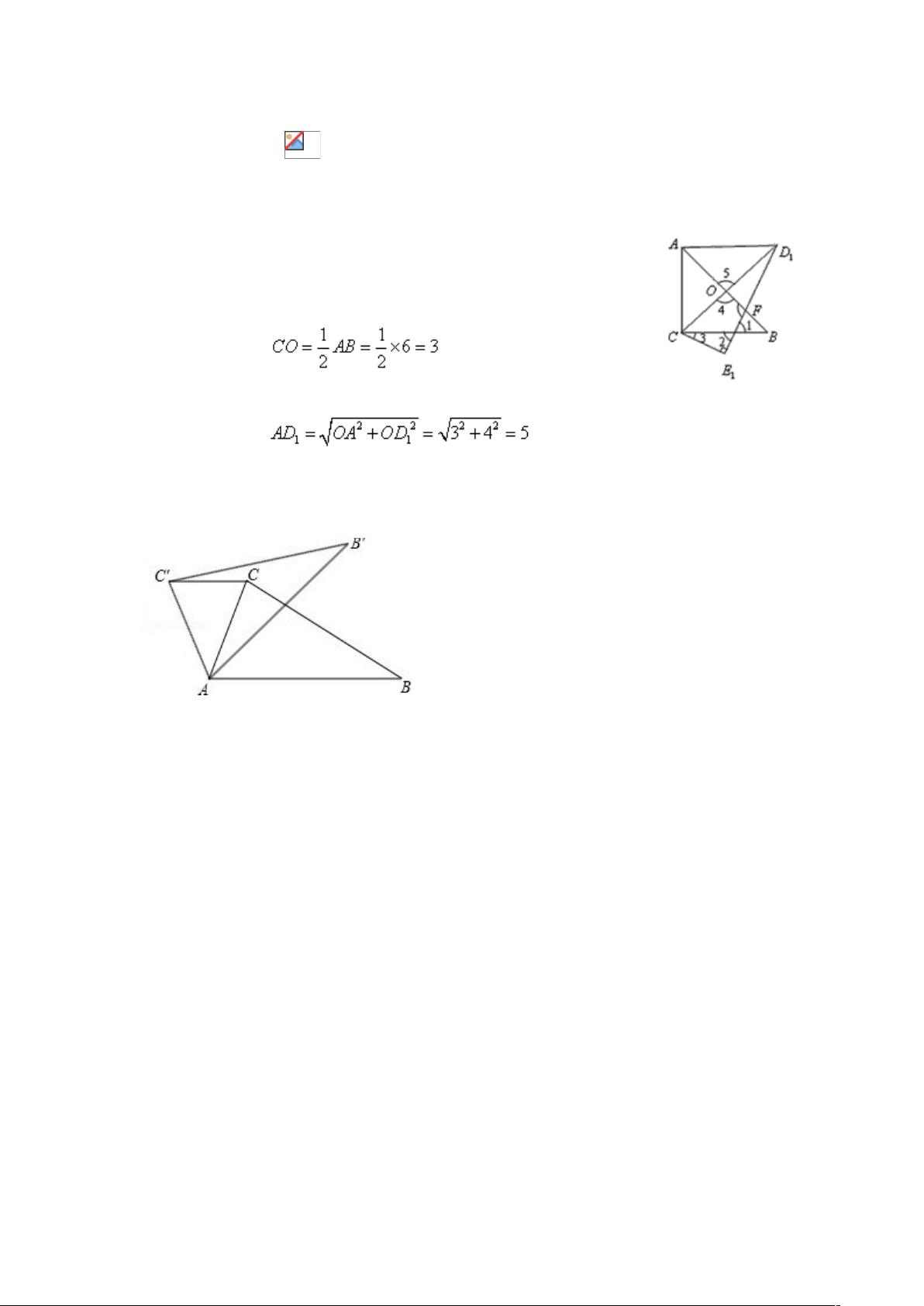
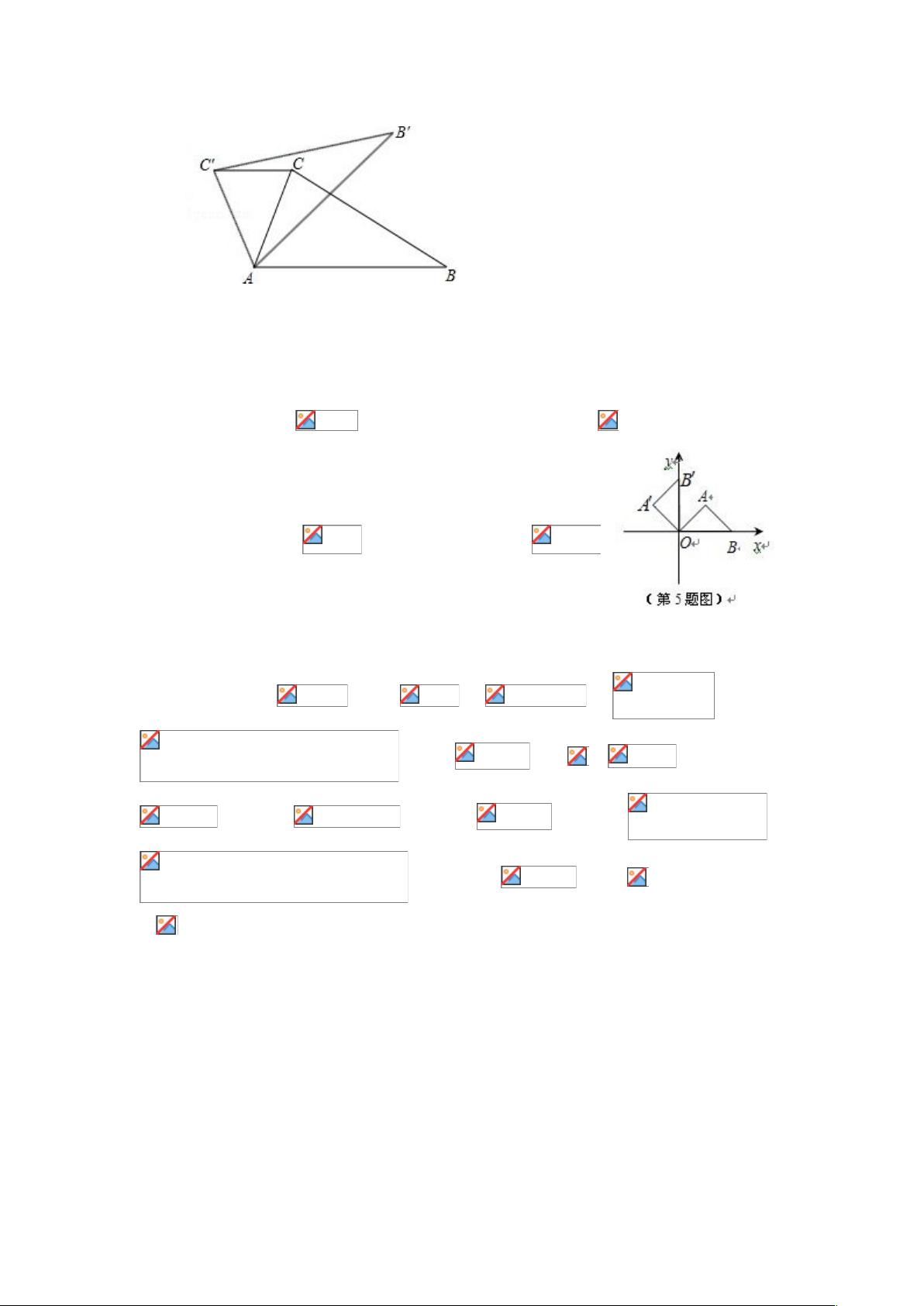
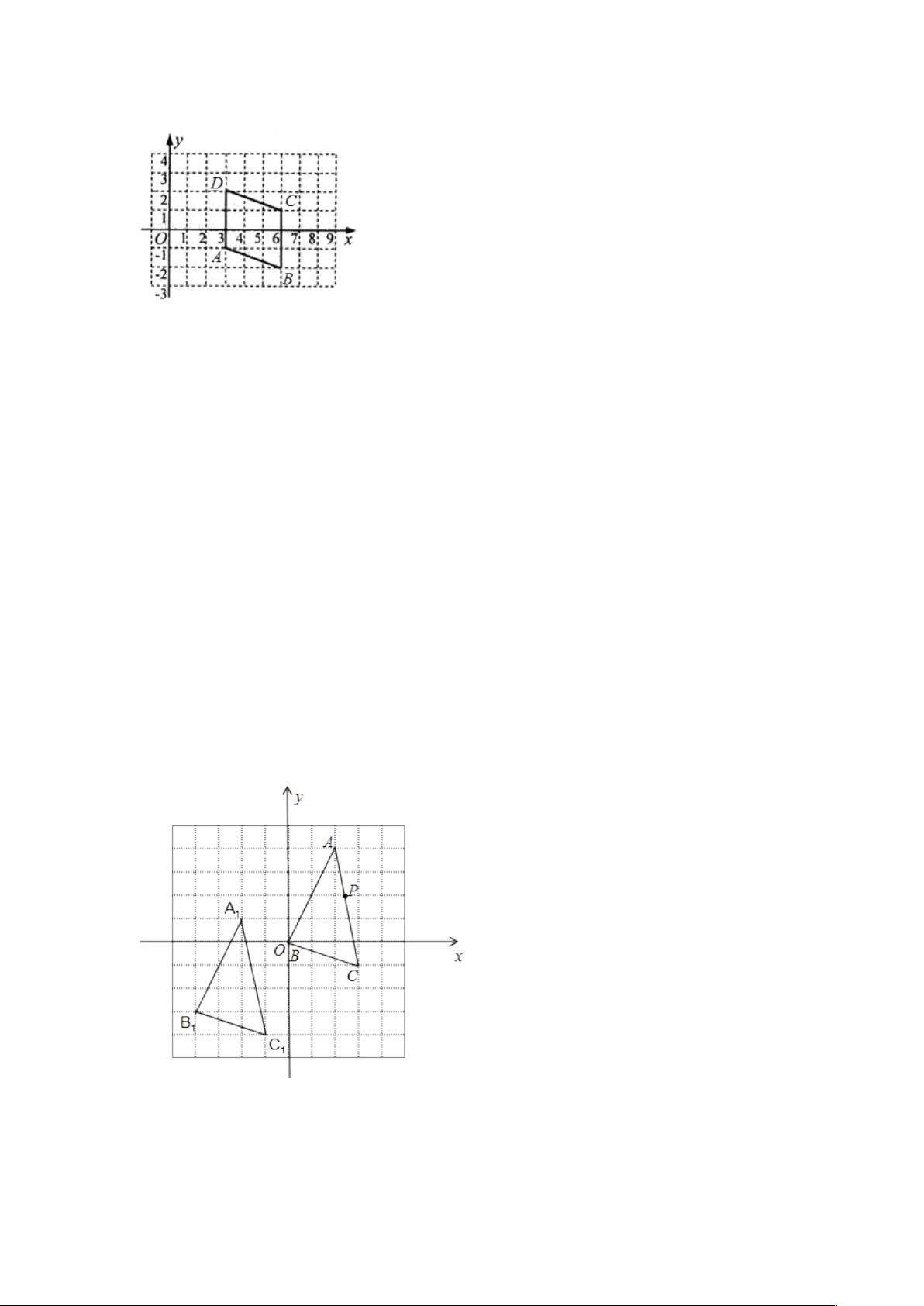
在深入分析《中考数学试题分类汇编514精选.doc》文档中的精选题型时，我们能洞察到其中蕴含的几何变换知识点与应用技巧，这对于初中生来说是一个挑战与提升空间观念和逻辑推理能力的良好机会。接下来，让我们详细探讨这些知识点，并了解它们如何在具体题目中被应用。 **全等变换**是几何问题解决中的一个重要概念，它分为平移、旋转和翻折三种形式。在几何题目中，全等变换的应用主要体现在保持图形的形状和大小不变的前提下，通过移动图形来证明或推断四边形的性质。例如，在证明一个四边形是矩形、菱形或平行四边形时，我们可以通过图形的全等变换来直观展示图形的对称性或角度关系，这是解决相关几何问题的重要手段。 **旋转的性质**是全等变换中的一个重要方面。通过旋转操作，学生可以观察图形在不同角度下的相互关系，进而判断角度关系或证明图形的特定性质。例如，在某个题目中，通过绕某一点旋转一定角度后，图形能够重合，从而可以利用这一性质来验证图形是否具备矩形或其他四边形的特性。 关于**矩形的判定**，我们通常依据其对角线的特性来判断。一个四边形若为矩形，则其对角线不仅互相平分，而且长度相等。在文档中的第1题，就涉及到了对角线的性质，需要证明四边形的一组对角线满足这些条件，结合等腰三角形的性质，可以推断出该四边形是矩形。 **等腰三角形的性质**是中考数学中经常被考查的内容之一。等腰三角形的两个底角相等，顶角平分底边，这一点在许多几何题目中被用来求解角度问题。第3题便利用了等腰三角形的这一特性，来求解图形中的特定角度值。 **平移的性质**是坐标几何中的一个基础知识点。图形的平移操作只改变点的横纵坐标，但不改变点的顺序和距离。在解决问题时，例如文档中的第5题，通过平移后的坐标，可以确定新位置上顶点的坐标值。 **旋转的坐标变化**则是更高阶的应用。在坐标系中，点绕原点旋转会遵循一定的变换规则，其坐标值会因旋转角度而发生相应的改变。在文档的第6题中，点P经过一系列的平移和旋转，其新坐标需要依照旋转中心和旋转角度进行精确计算。 **图形变换与坐标的关系**是解决几何问题的关键。无论是平移还是旋转，图形变换都会影响到图形上各点的坐标。掌握这一关系有助于学生更好地理解几何图形的变化规律，同时也有助于解决实际问题，如计算图形的位置、求解面积、周长等。 这些知识点在中考数学试题中扮演着重要的角色。通过对《中考数学试题分类汇编514精选.doc》文档的学习，学生不仅能够加深对几何变换的理解，还能够学会如何将这些理论知识应用到实际问题中去，这对于培养学生的空间想象力和逻辑推理能力具有极大的帮助。因此，系统地掌握这些知识点，将极大地提升学生解决数学问题的综合能力。