没有合适的资源?快使用搜索试试~ 我知道了~
中考数学试卷分类汇编417精选.doc
1.该资源内容由用户上传,如若侵权请联系客服进行举报
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
版权申诉
0 下载量 195 浏览量
2021-09-25
19:41:48
上传
评论
收藏 3.07MB DOC 举报
温馨提示
这些题目和解析主要涉及中考数学中的平行四边形相关知识点,包括平行四边形的性质、等腰三角形的判定、相似三角形的性质及其应用、勾股定理以及平行四边形的判定方法。 1. **平行四边形的性质**:平行四边形的对边平行且相等,对角相等,邻角互补。例如,在题目中提到的平行四边形ABCD中,AB=CD,AD=BC,并且∠A+∠B=180°。 2. **等腰三角形的判定与性质**:当一个角的平分线与对边相交时,可以证明形成的三角形是等腰三角形。例如,题目中指出∠BAD的平分线交BC于点E,因此,可以推出△ADF是等腰三角形,AD=DF。 3. **相似三角形的判定与性质**:两个三角形相似,它们的对应边成比例,面积比等于对应边的比例的平方。例如,题目中提到△DEF与△BAF相似,通过面积比例S△DEF:S△ABF=4:25,可以找到对应边的比例DE:AB=2:5。 4. **勾股定理**:在直角三角形中,斜边的平方等于两直角边的平方和。在第四个题目中,利用BG垂直于AE,通过勾股定理计算AG和AE的长度。 5. **平行四边形的判定**:可以通过对角线互相平分,两组对边平行或相等来判定一个四边形是平行四边形。第五个题目中,条件AB∥DC,AD=BC并不能直接判定四边形ABCD是平行四边形,因为只满足了一组对边平行,但另一组对边不相等。 这些题目展示了中考数学中平行四边形部分的重要知识点和解题技巧,包括几何图形的性质分析、比例关系的应用以及计算能力的考察。学生在复习这部分内容时,应重点理解平行四边形的性质,熟练掌握等腰三角形和相似三角形的判定与性质,同时运用勾股定理解决实际问题。
资源详情
资源评论
资源推荐
2013 中考全国 100 份试卷分类汇编
平行四边形
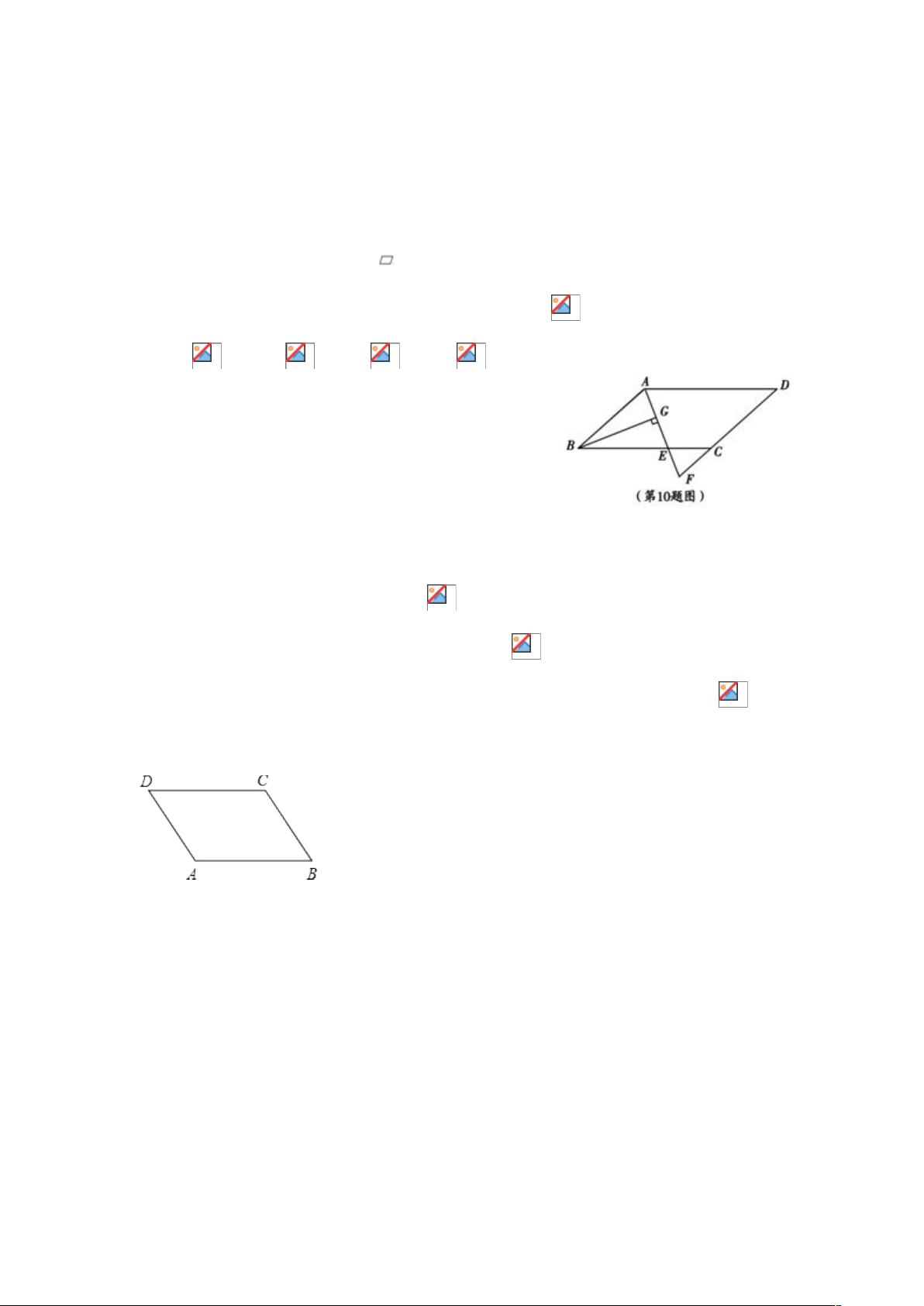
1、(德阳市 2013 年)如图.在 ABCD 中,AB=6、AD=9,∠BAD 的平分线交 BC 于
点 E,DC 的延长线于点 F, BG⊥AE,垂足为 G,若 BG=4 ,则△CEF 的面积是
A、2 B、 C、3 D、4
答案:A
解 析 : ∵ 在 ▱ ABCD 中 ,
AB=CD=6 , AD=BC=9 , ∠ BAD 的 平 分 线 交 BC 于 点
E,
BAF= DAF∴∠ ∠ ,∵AB DF∥ ,∠BAF= F∠ ,∴∠F= DA∠
F,
ADF∴△ 是等腰三角形,AD=DF=9;∵AB=CD=6, ∴CF=3;
∠BEA=∠DAF=∠BAF,所以,BA=BE,
∴在△ABG 中,BG AE⊥ ,AB=6,BG=4 可得:AG=2,
又∵BG AE⊥ ,∴AE=2AG=4,∴△ABE 的面积等于 8 ,
又∵▱ABCD,∴△CEF BEA∽△ ,相似比为 1:2,面积 1:4,∴△CEF 的面积为,2 .
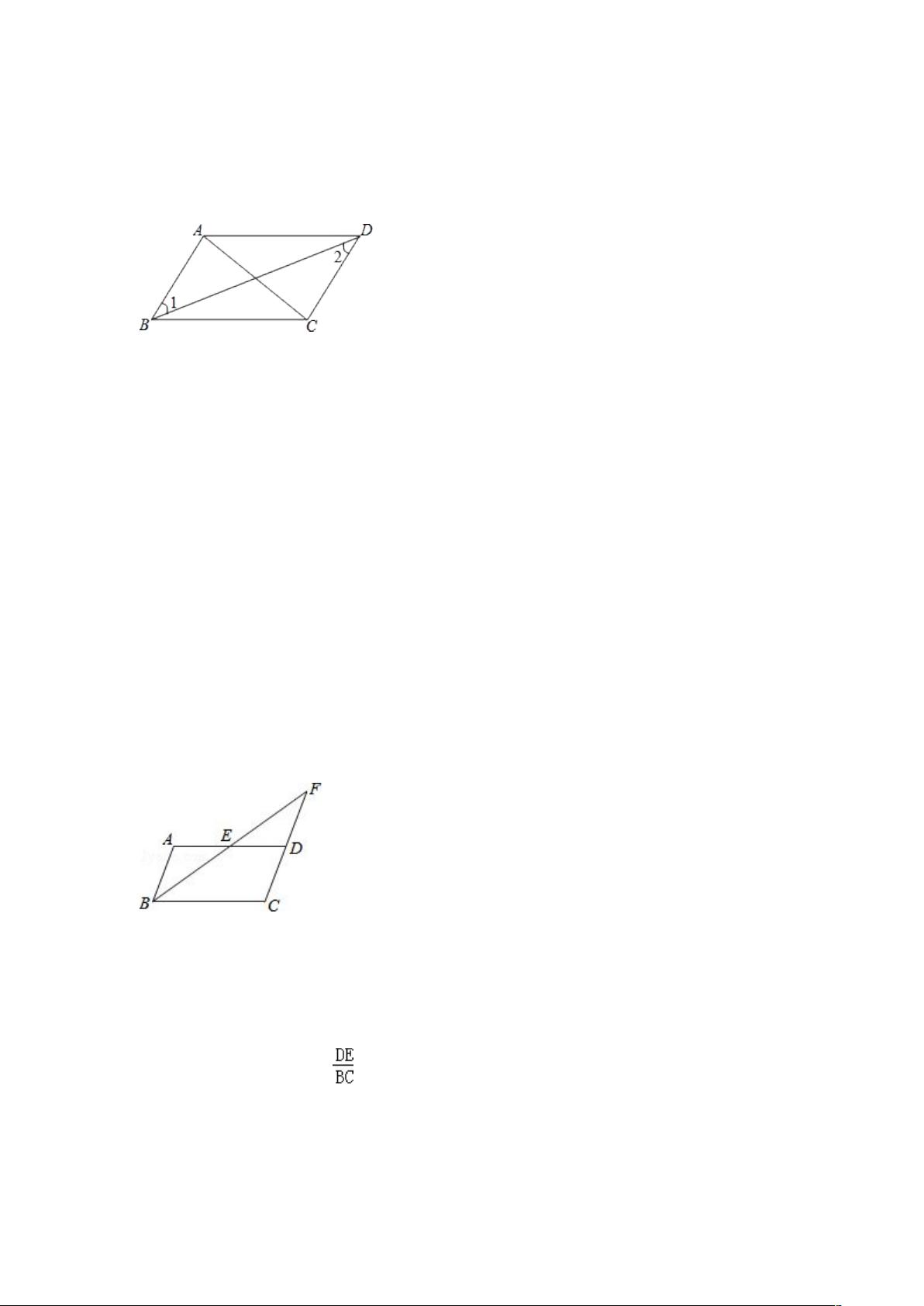
2、(2013 杭州)在▱ABCD 中,下列结论一定正确的是( )
A.AC BD⊥ B.∠A+ B=180°∠ C.AB=AD D.∠A≠ C∠
考点:平行四边形的性质.
分析:由四边形 ABCD 是平行四边形,可得 AD BC∥ ,即可证得∠A+ B=180°∠ .
解答:解:∵四边形 ABCD 是平行四边形,
AD BC∴ ∥ ,
A+ B=180°∴∠ ∠ .
故选 B.
点评:此题考查了平行四边形的性质.此题比较简单,注意掌握数形结合思想的应用.
3、(2013•内江)如图,在▱ABCD 中,E 为 CD 上一点,连接 AE、BD,且 AE、BD 交于
点 F,S
DEF△
:S
ABF△
=4:25,则 DE:EC=( )
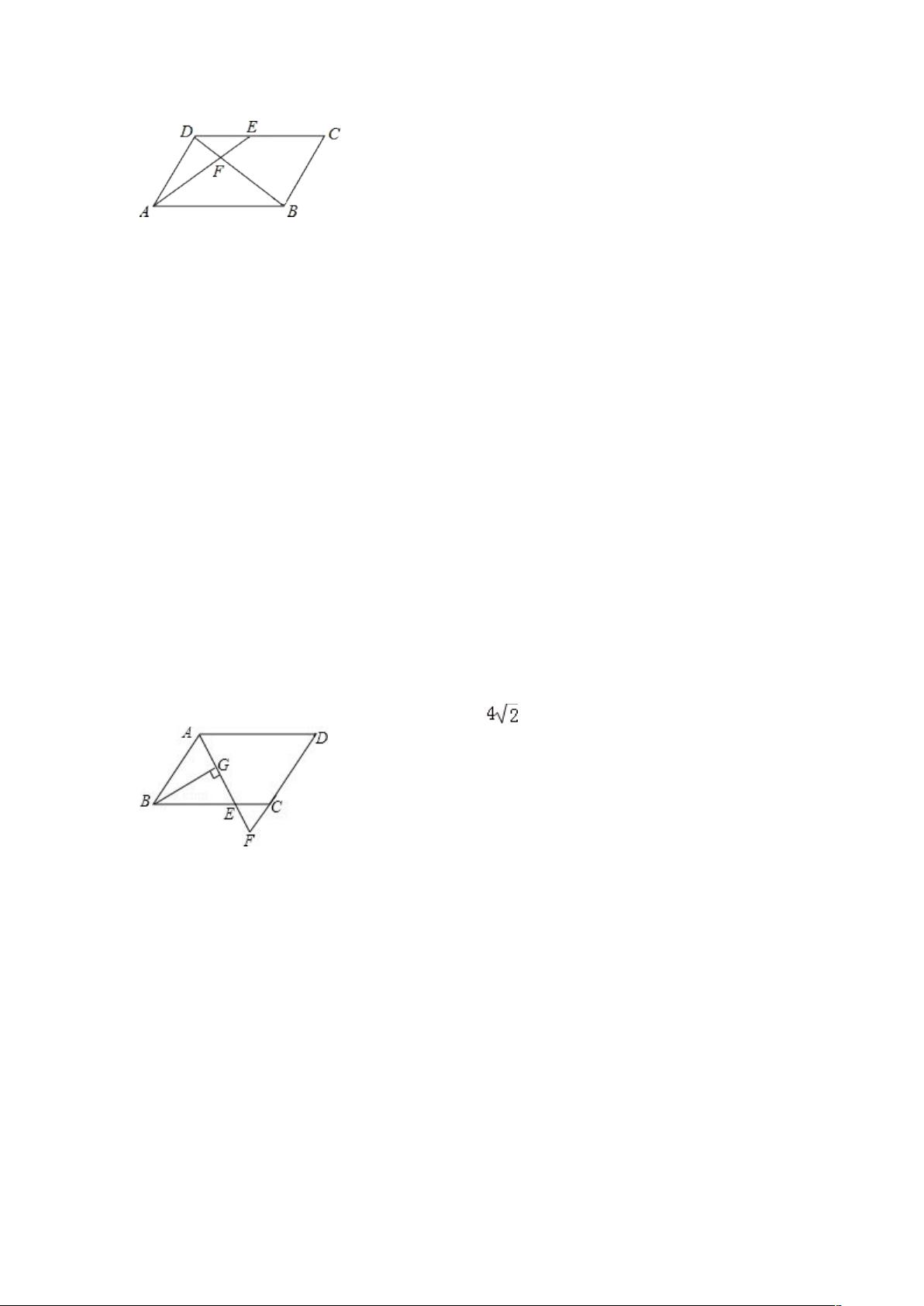
A.2:5 B.2:3 C.3:5 D.3:2
考
点:
相似三角形的判定与性质;平行四边形的性质.
分
析:
先根据平行四边形的性质及相似三角形的判定定理得出△DEF BAF∽△ ,再根据
S
DEF△
:S
ABF△
=4:10:25 即可得出其相似比,由相似三角形的性质即可求出 DE:
EC 的值,由 AB=CD 即可得出结论.
解
答:
解:∵四边形 ABCD 是平行四边形,
AB CD∴ ∥ ,
EAB= DEF∴∠ ∠ ,∠AFB= DFE∠ ,
DEF BAF∴△ ∽△ ,
S∵
DEF△
:S
ABF△
=4:25,
DE∴ :AB=2:5,
AB=CD∵ ,
DE∴ :EC=2:3.
故选 B.
点
评:
本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长
的比等于相似比,面积的比等于相似比的平方是解答此题的关键.
4、(2013•自贡)如图,在平行四边形 ABCD 中,AB=6,AD=9,∠BAD 的平分线交 BC
于 E,交 DC 的延长线于 F,BG AE⊥ 于 G,BG= ,则△EFC 的周长为( )
A.
11
B.
10
C.
9
D.
8
考
点:
相似三角形的判定与性质;勾股定理;平行四边形的性质.3718684
分
析:
判断出△ADF 是等腰三角形,△ABE 是等腰三角形,DF 的长度,继而得到 EC 的长
度,在 Rt BGE△ 中求出 GE,继而得到 AE,求出△ABE 的周长,根据相似三角形的
周长之比等于相似比,可得出△EFC 的周长.
解
答:
解:∵在▱ABCD 中,AB=CD=6,AD=BC=9,∠BAD 的平分线交 BC 于点 E,
BAF= DAF∴∠ ∠ ,
AB DF∵ ∥ ,AD BC∥ ,
BAF= F= DAF∴∠ ∠ ∠ ,∠BAE= AEB∠ ,
AB=BE=6∴ ,AD=DF=9,
ADF∴△ 是等腰三角形,△ABE 是等腰三角形,
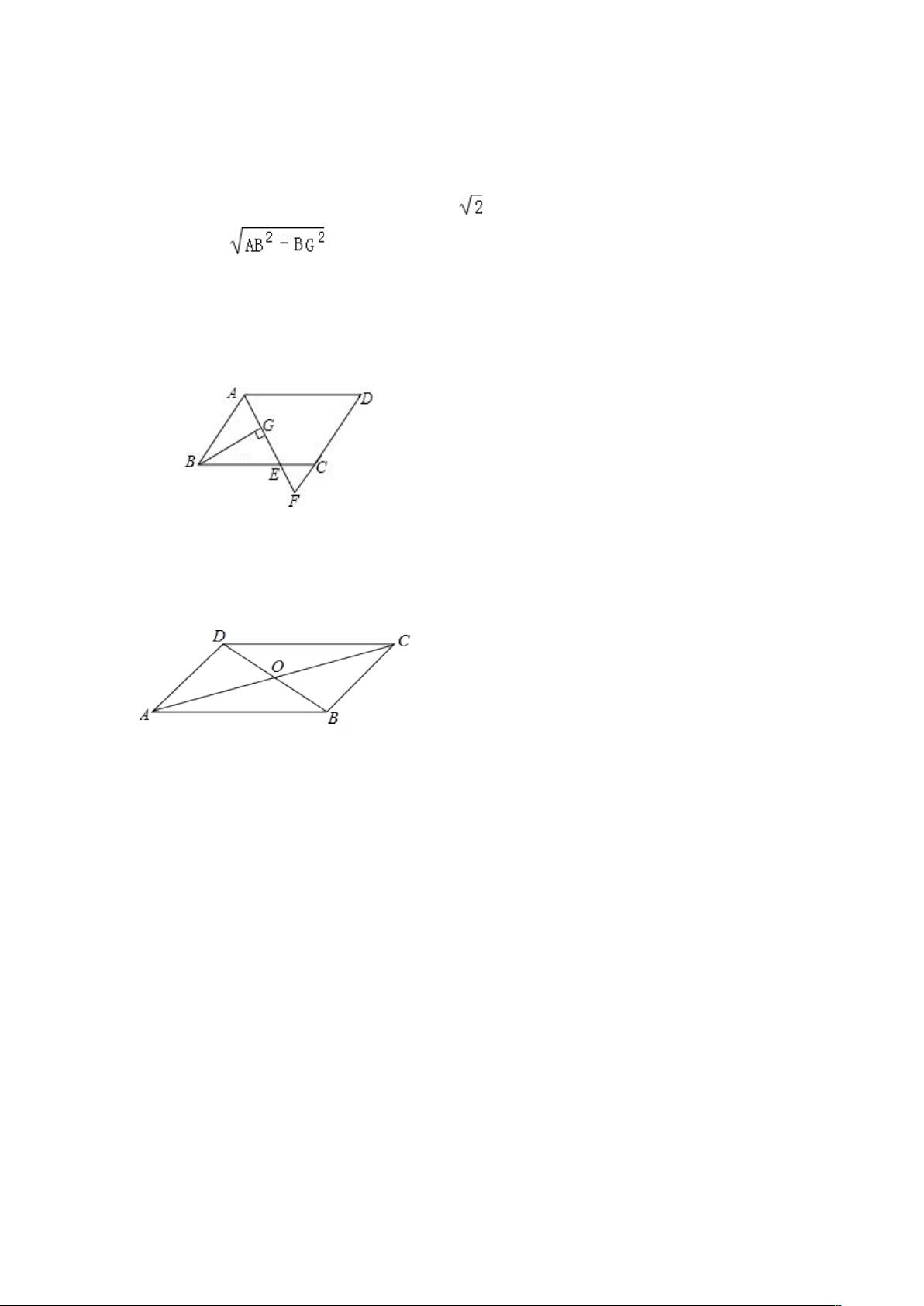
AD BC∵ ∥ ,
EFC∴△ 是等腰三角形,且 FC=CE,
EC=FC=9 6=3∴ ﹣ ,
在△ABG 中,BG AE⊥ ,AB=6,BG=4 ,
AG=∴ =2,
AE=2AG=4∴ ,
ABE∴△ 的周长等于 16,
又∵△CEF BEA∽△ ,相似比为 1:2,
CEF∴△ 的周长为 8.
故选 D.
点
评:
本题主要考查了勾股定理、相似三角形、等腰三角形的性质,注意掌握相似三角形
的周长之比等于相似比,此题难度较大.
5、(2013•泸州)四边形 ABCD 中,对角线 AC、BD 相交于点 O,下列条件不能判定这个
四边形是平行四边形的是( )
A.AB DC∥ ,AD BC∥ B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB DC∥ ,AD=BC
考
点:
平行四边形的判定.
分
析:
根据平行四边形判定定理进行判断.
解
答:
解:A、由“AB DC∥ ,AD BC”∥ 可知,四边形 ABCD 的两组对边互相平行,则该四边
形是平行四边形.故本选项不符合题意;
B、由“AB=DC,AD=BC”可知,四边形 ABCD 的两组对边相等,则该四边形是平行
四边形.故本选项不符合题意;
C、由“AO=CO,BO=DO”可知,四边形 ABCD 的两条对角线互相平分,则该四边形
是平行四边形.故本选项不符合题意;
D、由“AB DC∥ ,AD=BC”可知,四边形 ABCD 的一组对边平行,另一组对边相等,
据此不能判定该四边形是平行四边形.故本选项符合题意;
故选 D.
点
评:
本题考查了平行四边形的判定.
(1)两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
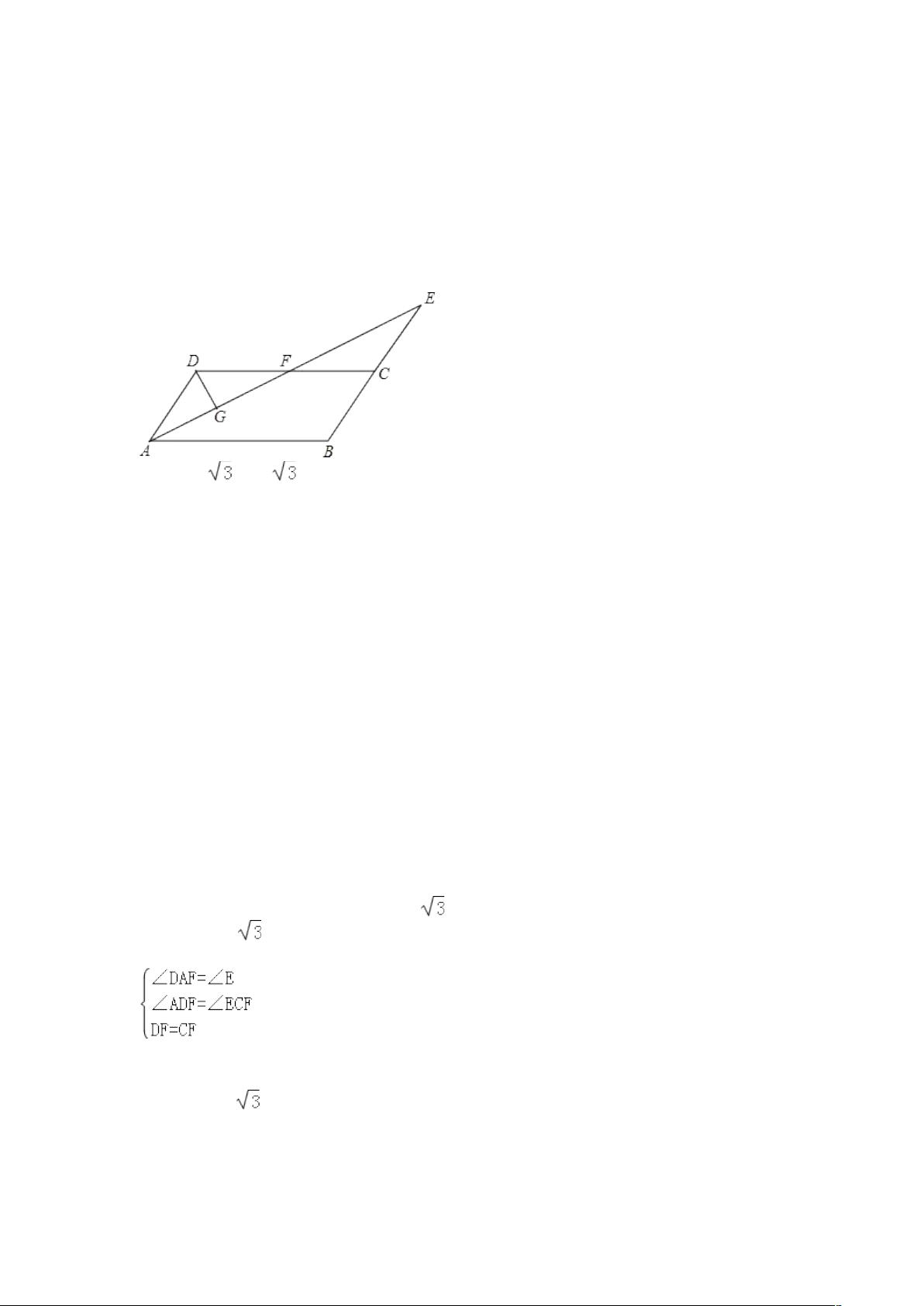
6、(2013 泰安)如图,在平行四边形 ABCD 中,AB=4,∠BAD 的平分线与 BC 的延长线
交于点 E,与 DC 交于点 F,且点 F 为边 DC 的中点,DG AE⊥ ,垂足为 G,若 DG=1,则
AE 的边长为( )
A.2 B.4 C.4 D.8
考点:平行四边形的性质;等腰三角形的判定与性质;含 30 度角的直角三角形;勾股定理.
专题:计算题.
分析:由 AE 为角平分线,得到一对角相等,再由 ABCD 为平行四边形,得到 AD 与 BE 平
行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到 AD=DF,由
F 为 DC 中点,AB=CD,求出 AD 与 DF 的长,得出三角形 ADF 为等腰三角形,根据三线
合一得到 G 为 AF 中点,在直角三角形 ADG 中,由 AD 与 DG 的长,利用勾股定理求出
AG 的长,进而求出 AF 的长,再由三角形 ADF 与三角形 ECF 全等,得出 AF=EF,即可求
出 AE 的长.
解答:解:∵AE 为∠ADB 的平分线,
DAE= BAE∴∠ ∠ ,
DC AB∵ ∥ ,
BAE= DFA∴∠ ∠ ,
DAE= DFA∴∠ ∠ ,
AD=FD∴ ,
又 F 为 DC 的中点,
DF=CF∴ ,
AD=DF=DC=AB=2∴ ,
在 Rt ADG△ 中,根据勾股定理得:AG= ,
则 AF=2AG=2 ,
在△ADF 和△ECF 中,
,
ADF ECF∴△ ≌△ (AAS),
AF=EF∴ ,
则 AE=2AF=4 .
故选 B
点评:此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形
的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.
7、(2013•益阳)如图,在平行四边形 ABCD 中,下列结论中错误的是( )
A.
1= 2∠ ∠
B.
BAD= BCD∠ ∠
C.
AB=CD
D.
AC BD⊥
考
点:
平行四边形的性质.
分
析:
根据平行四边形的性质,平行四边形对边平行以及对边相等和对角相等分别判断得
出即可.
解
答:
解:∵在平行四边形 ABCD 中,
AB CD∴ ∥ ,
1= 2∴∠ ∠ ,故此选项正确,不合题意;
∵四边形 ABCD 是平行四边形,
BAD= BCD∴∠ ∠ ,AB=CD,故 B,C 选项正确,不合题意;
无法得出 AC BD⊥ ,故此选项错误,符合题意.
故选 D.
点
评:
此题主要考查了平行四边形的性质,熟练掌握相关的性质是解题关键.
8、(2013•湘西州)如图,在▱ABCD 中,E 是 AD 边上的中点,连接 BE,并延长 BE 交
CD 延长线于点 F,则△EDF 与△BCF 的周长之比是( )
A.1:2 B.1:3 C.1:4 D.1:5
考
点:
平行四边形的性质;全等三角形的判定与性质
分
析:
根据平行四边形性质得出 AD=BC,AD BC∥ ,推出△EDF BCF∽△ ,得出△EDF 与
△BCF 的周长之比为 ,根据 BC=AD=2DE 代入求出即可.
解
答:
解:∵四边形 ABCD 是平行四边形,
AD=BC∴ ,AD BC∥ ,
EDF BCF∴△ ∽△ ,
剩余30页未读,继续阅读
CSGOGOTO
- 粉丝: 38
- 资源: 27万+
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- Linux环境下Nginx服务器的源码安装与自动启动配置指南
- 【Unity 插件】DLSS - Upscaling for Unity 将低分辨率图像提升为高分辨率图像,接近或超越原生分辨率
- 基于角色访问控制的Linux安全模块+项目源码+文档说明
- 基于uniapp构建的顺风车、约车、拼车、通勤、滴滴微信小程序(源码+文档说明)
- 【Unity 插件】Invector FSM AI Template 易用的 AI 模板, 轻松实现敌人的巡逻、追击、攻击等动作
- 文本数据可视化tocsv.csv
- 基于HSV色彩空间和樽海鞘群优化算法的低照度图像增强
- Fine-BI考试全量题库(含答案)
- yolo的xtx数据集增强
- 技术资料分享RDA5820很好的技术资料.zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0