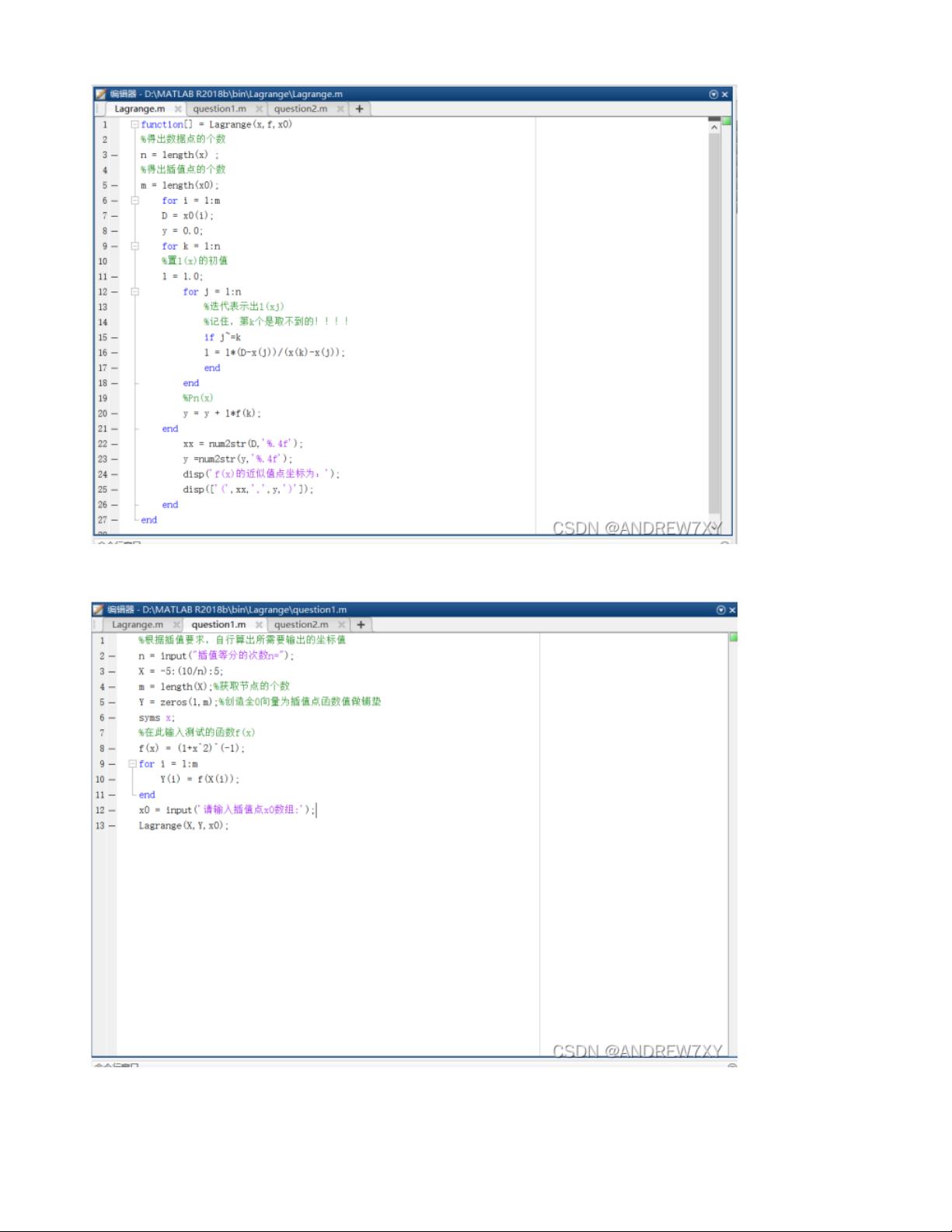
拉格朗日插值法是一种在数学和计算机科学中广泛使用的数值分析技术，它通过构建一个多项式函数来近似给定数据点的分布。在MATLAB中，我们可以利用编程来实现这一方法，以帮助我们预测或拟合数据点之间的关系。本文将深入探讨拉格朗日插值法的基本原理，MATLAB的实现方式，以及如何通过实例来理解和应用这种方法。
拉格朗日插值法基于以下思想：给定n+1个不同的离散点(x_0, y_0), (x_1, y_1), ..., (x_n, y_n)，存在唯一的n次多项式P_n，使得P_n在每个点上都与这些数据点一致。这个多项式可以表示为：
\[ P_n(x) = \sum_{i=0}^{n} y_i L_i(x) \]
其中，\( L_i(x) \)是拉格朗日基多项式，定义为：
\[ L_i(x) = \prod_{j=0, j \neq i}^{n} \frac{x - x_j}{x_i - x_j} \]
在MATLAB中，我们可以编写一个函数来计算拉格朗日插值。以下是一个简单的实现示例：
```matlab
function y = lagrangeInterpolation(x, y, xi)
n = length(x);
y_interpolated = zeros(1, length(xi));
for k = 1:length(xi)
L = 1;
for i = 1:n
if i ~= k
L = L * (xi(k) - x(i)) / (x(k) - x(i));
end
end
y_interpolated(k) = L * y(k);
end
end
```
这个函数接受三个参数：数据点的x坐标数组，对应的y坐标数组，以及需要进行插值的x坐标xi。函数内部通过循环和乘法计算出每个L_i(x)，并最终得到插值结果y_interpolated。
为了更好地理解这一方法，我们可以考虑一个简单的实例。比如，我们有以下四个数据点：(-1, 2), (0, 0), (1, 3), (2, 4)，并希望在x=0.5处进行插值。在MATLAB中，我们可以这样操作：
```matlab
x = [-1, 0, 1, 2];
y = [2, 0, 3, 4];
xi = 0.5;
y_interpolated = lagrangeInterpolation(x, y, xi);
disp(y_interpolated);
```
这将输出在x=0.5处的插值结果。
通过拉格朗日插值法，我们可以对非线性数据进行平滑处理，预测未知点的值，或者在有限的数据集上构造连续函数。然而，需要注意的是，当数据点过多时，这种方法可能导致振荡和过拟合。因此，在实际应用中，需要权衡插值的精度和稳定性。
在提供的PDF文档《拉格朗日插值法MATLAB实现（附代码、实例、详解）》中，读者可以找到更详细的解释，包括更多实例、代码注解以及对插值效果的可视化展示，有助于进一步理解和掌握拉格朗日插值法在MATLAB中的具体应用。
