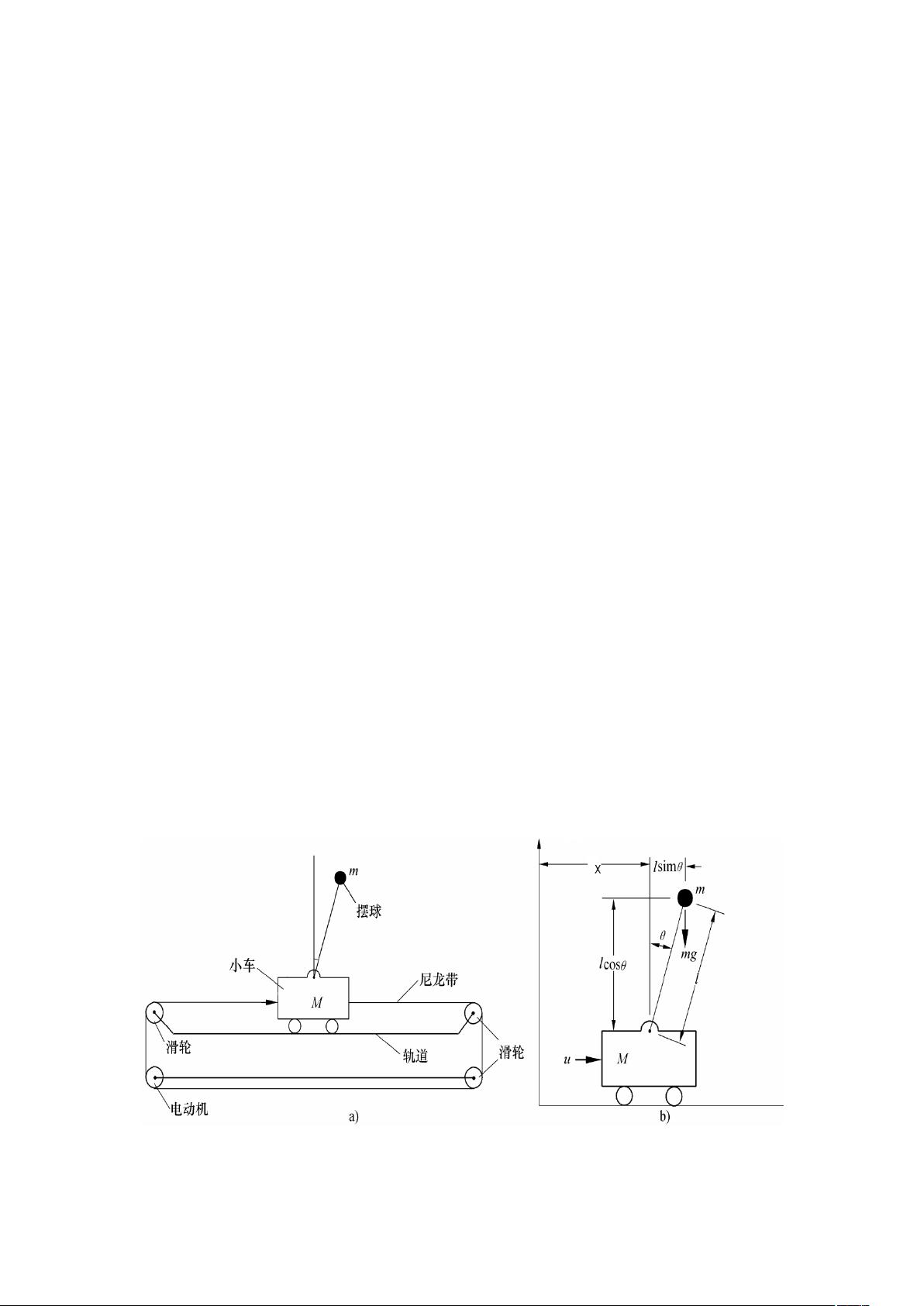
倒立摆在matlab的simulink库下的仿真.doc

倒立摆在 matlab 的 simulink 库下的仿真 一、倒立摆系统的组成和控制原理 倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统。研究倒立摆控制能有效地反映控制中的许多问题，倒立摆研究具有重要的理论价值和应用价值。在自动化领域中具有重要的价值。 二、倒立摆系统的数学模型 倒立摆系统的数学模型可以用小车的位移和速度及杆偏离垂线的角度 θ 和角速度来描述。设小车位移为 x，那么小球中心位置是在水平方向，应用牛顿第二定律： $$M \ddot{x} = M g \sin \theta - m g \sin \theta - u$$ $$m l \ddot{\theta} = m g \sin \theta - m l \ddot{x} \sin \theta + u$$ 线性化： $$\dot{x} = Ax + Bu$$ $$y = Cx + Du$$ 其中，A、B、C、D 是状态空间模型的矩阵，x 是状态变量，u 是输入，y 是系统的输出。 三、单级倒立摆系统的状态空间模型 单级倒立摆系统的状态空间模型可以用小车的位移、小车的速度、小车的角度、小车的角速度分别为状态变量： $$x = [x_1, x_2, x_3, x_4]^T$$ $$u = [u_1, u_2]^T$$ $$y = [y_1, y_2]^T$$ 状态空间模型的矩阵 A、B、C、D 可以通过解微分方程式获得。 四、倒立摆系统的极点配置 倒立摆系统的极点配置可以通过 MATLAB/Simulink 仿真获得。在 MATLAB 中输入命令，可以得到状态反应矩阵。然后，可以通过状态反应来任意配置极点。 五、倒立摆系统的仿真模型 倒立摆系统的仿真模型可以通过 MATLAB/Simulink 构造单级倒立摆状态反应控制系统的仿真模型。在 Simulink 中，可以设计状态空间模型，并且可以通过状态反应来配置极点。 六、结论 本文研究了倒立摆系统的控制问题，并且设计了单级倒立摆状态反应控制系统的仿真模型。在 MATLAB/Simulink 中，可以通过状态反应来配置极点，并且可以实现倒立摆系统的控制。