01 第1章 控制系统状态空间表达式（4：3）.pptx

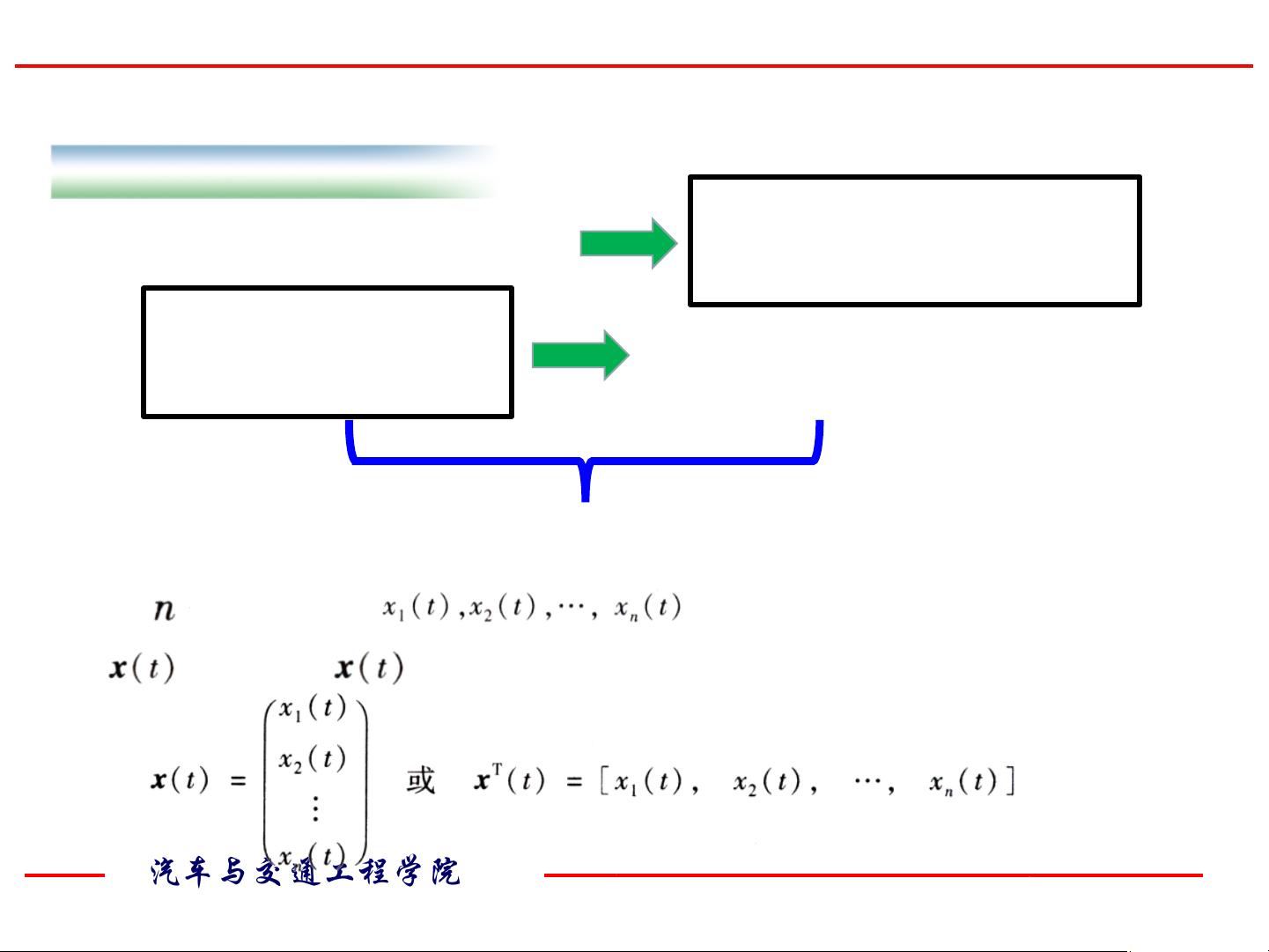
### 控制系统状态空间表达式概述 #### 1.1 状态变量及状态空间表达式 **1.1.1 状态变量性质** 状态变量是一组可以唯一确定系统当前状态的变量集合。对于一个给定的系统，状态变量的选择不是唯一的，但必须满足以下条件： - 必须能够充分描述系统在任意时刻的状态。 - 是一组最小数量的变量，能够完全确定系统状态。 **1.1.2 状态矢量** 如果系统的状态由\( n \)个状态变量组成，这些变量可以被看作一个\( n \)-维向量\(\mathbf{x}\)，即状态矢量。例如，如果一个系统有两个状态变量\( x_1 \)和\( x_2 \)，则状态矢量可以表示为\(\mathbf{x} = [x_1, x_2]^T\)。 状态矢量\(\mathbf{x}(t)\)随时间变化，且在任意时刻\( t \)的状态\(\mathbf{x}(t)\)可以通过初始状态\(\mathbf{x}(t_0)\)和从\( t_0 \)到\( t \)的所有输入\(\mathbf{I}(t)\)来确定。数学上可以表示为： \[ \mathbf{x}(t) = f(\mathbf{x}(t_0), \mathbf{I}(t)) \] **1.1.3 状态空间** 状态空间是由所有可能的状态矢量构成的\( n \)-维空间。每一个状态变量对应一个坐标轴，因此状态空间是一个几何空间，其中的每一点代表系统的一个可能状态。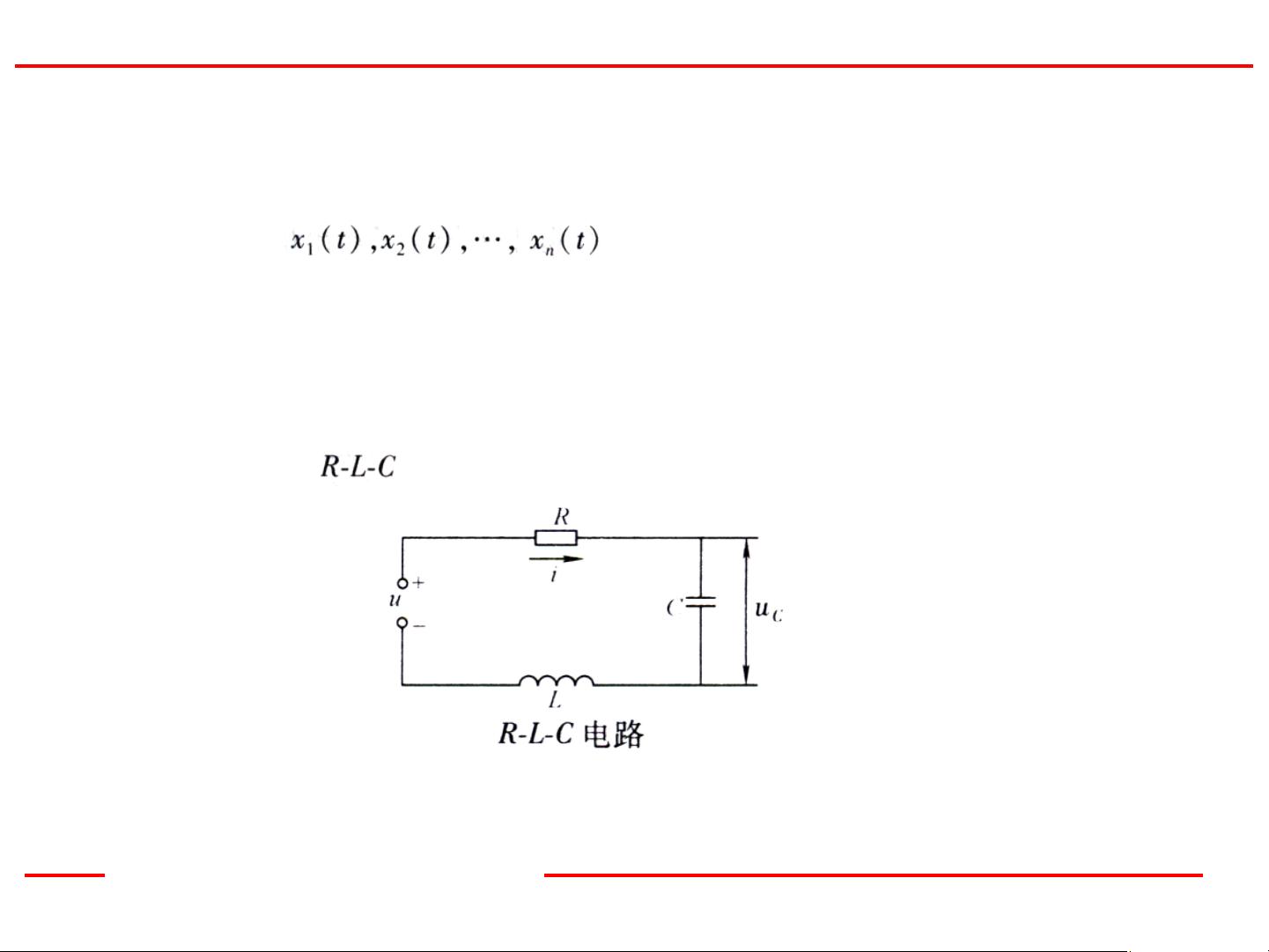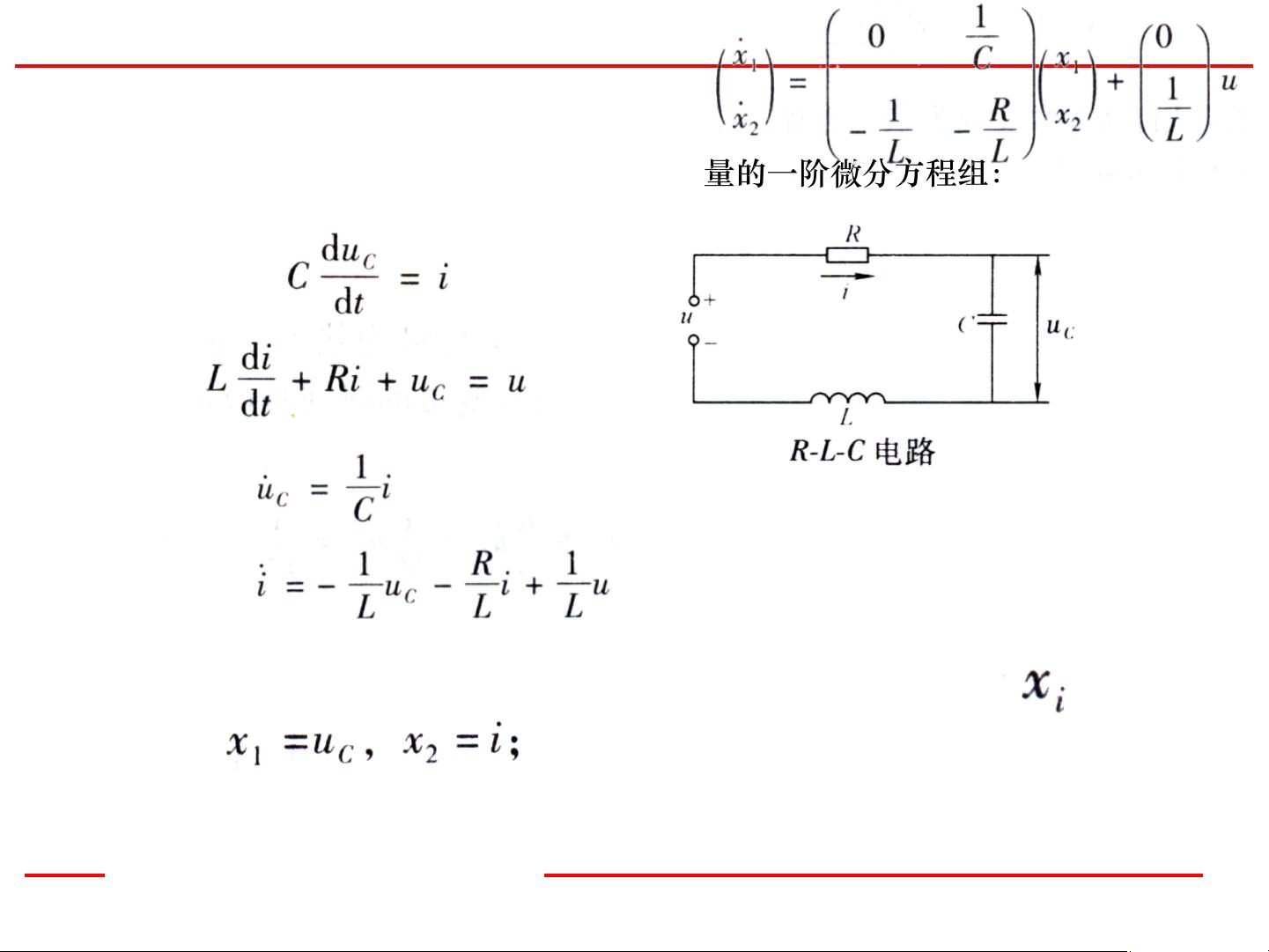 **1.1.4 状态方程** 状态方程是描述系统状态变化规律的一阶微分方程组。假设一个简单的例子，如图所示的电路，可以写出两个包含状态变量的一阶微分方程组： \[ \dot{x}_1 = -\frac{1}{RC}x_1 + \frac{1}{C}u \] \[ \dot{x}_2 = -\frac{1}{RC}x_2 + \frac{1}{C}x_1 \] 这里，\( u \)是输入信号，\( R \)和\( C \)分别是电阻和电容值。\(\dot{x}_1\)和\(\dot{x}_2\)分别是状态变量\( x_1 \)和\( x_2 \)关于时间的导数。将状态方程写成矢量矩阵形式，可以简化为： \[ \dot{\mathbf{x}} = A\mathbf{x} + B\mathbf{u} \] **1.1.5 输出方程** 输出方程描述了系统输出与状态变量之间的关系。例如，对于上面的例子，如果输出\( y \)定义为\( x_2 \)，则输出方程可以写为： \[ y = C^T\mathbf{x} + D\mathbf{u} \] **1.1.6 状态空间表达式** 状态空间表达式由状态方程和输出方程组成，是描述系统动态行为的一种强大工具。对于单输入单输出的系统，状态空间表达式的一般形式为： \[ \dot{\mathbf{x}} = A\mathbf{x} + B\mathbf{u} \] \[ \mathbf{y} = C^T\mathbf{x} + D\mathbf{u} \] 对于多输入多输出系统，状态空间表达式的矢量矩阵形式为： \[ \dot{\mathbf{x}} = A\mathbf{x} + B\mathbf{u} \] \[ \mathbf{y} = C\mathbf{x} + D\mathbf{u} \] 其中，\(\mathbf{x}\)为\( n \)-维状态矢量，\( A \)为\( n \times n \)系统矩阵，\( \mathbf{u} \)为\( r \)-维输入矢量，\( \mathbf{y} \)为\( m \)-维输出矢量，\( B \)、\( C \)和\( D \)为适当的矩阵。 #### 1.2 状态变量及状态空间表达式的模拟结构图 状态空间表达式的模拟结构图是一种图形化表示方法，用于直观展示系统内部信号的流动情况。绘制模拟结构图的基本步骤包括： - 确定所需的积分器数量，这应该与状态变量的数量相同； - 根据状态方程和输出方程绘制加法器和比例器； - 使用箭头将这些组件连接起来，形成完整的系统模型。 例如，对于一个简单的一阶系统，其状态方程为\(\dot{x} = ax + bu\)，模拟结构图可以通过一个积分器和几个比例器和加法器来实现。 通过上述介绍可以看出，状态空间表达式为控制系统分析提供了一种强有力的数学框架，不仅可以清晰地表示系统的动态特性，还便于进行进一步的分析和设计。