
Vol.:(0123456789)
Artificial Intelligence Review (2024) 57:98
https://doi.org/10.1007/s10462-024-10723-4
1 3
Black‑winged kite algorithm: anature‑inspired
meta‑heuristic forsolving benchmark functions
andengineering problems
JunWang
1
· Wen‑chuanWang
1
· Xiao‑xueHu
1
· LinQiu
1
· Hong‑feiZang
1
Accepted: 4 February 2024
© The Author(s) 2024
Abstract
This paper innovatively proposes the Black Kite Algorithm (BKA), a meta-heuristic opti-
mization algorithm inspired by the migratory and predatory behavior of the black kite.
The BKA integrates the Cauchy mutation strategy and the Leader strategy to enhance the
global search capability and the convergence speed of the algorithm. This novel combina-
tion achieves a good balance between exploring global solutions and utilizing local infor-
mation. Against the standard test function sets of CEC-2022 and CEC-2017, as well as
other complex functions, BKA attained the best performance in 66.7, 72.4 and 77.8% of
the cases, respectively. The effectiveness of the algorithm is validated through detailed
convergence analysis and statistical comparisons. Moreover, its application in solving
five practical engineering design problems demonstrates its practical potential in address-
ing constrained challenges in the real world and indicates that it has significant competi-
tive strength in comparison with existing optimization techniques. In summary, the BKA
has proven its practical value and advantages in solving a variety of complex optimization
problems due to its excellent performance. The source code of BKA is publicly available at
https:// www. mathw orks. com/ matla bcent ral/ filee xchan ge/ 161401- black- winged- kite- algor
ithm- bka.
Keywords Nature-inspired optimization· Black-winged kite algorithm· Meta-heuristic·
Constrained proble
* Wen-chuan Wang
wangwen1621@163.com; wangwenchuan@ncwu.edu.cn
Jun Wang
wangjun20221121@163.com
Xiao-xue Hu
xiaoxue_2356@163.com
Lin Qiu
qiulin@ncwu.edu.cn
Hong-fei Zang
zhf6344@163.com
1
College ofWater Resources, North China University ofWater Resources andElectric Power,
Zhengzhou450046, China
Content courtesy of Springer Nature, terms of use apply. Rights reserved.

J.Wang et al.
1 3
98 Page 2 of 53
1 Introduction
In recent years, due to resource scarcity and increasing demand from people (Feng
et al. 2024), improving production efficiency has become a research hotspot (Zhao
etal. 2023a, b). As technology advances and problems become more complex, optimi-
zation tasks frequently exhibit multi-objective, large-scale, uncertain, and complicated
traits to parse (Wan etal. 2023). In the real world, many problems have multiple opti-
mization objectives and constraints, while traditional optimization algorithms (Inceyol
and Cay 2022; Wang etal. 2022) are mainly designed for a single objective or a small
number of objective issues (Atban etal. 2023; Hu etal. 2023; Wang etal. 2023a, b).
Traditional algorithms may not be able to accurately find the optimal solution when
faced with these challenging optimization tasks, or the solving procedure may be
overly complicated and time-consuming. Secondly, the search space for some prob-
lems is vast, and traditional optimization algorithms find it challenging to efficiently
search for the optimal solution in this situation. In addition, once the problem involves
uncertainty and fuzziness (Berger and Bosetti 2020), traditional optimization algo-
rithms cannot handle it well. This is because conventional optimization algorithms are
mainly based on deterministic assumptions and constraints. At the same time, there are
always uncertainties and randomness in areas such as venture capital (Xu etal. 2023a,
b), supply chain management (Zaman etal. 2023), and resource scheduling (Al-Masri
etal. 2023). Finally, traditional optimization algorithms typically rely on the analytical
form of the problem, which requires the problem to be clearly defined and described
in mathematical form (Kumar etal. 2023). In practical situations, it is often difficult
to express the problem analytically, or the problem’s objective function and constraint
conditions are intricate (Wang etal. 2020). In summary, traditional optimization algo-
rithms often cannot meet the needs and challenges of current optimization tasks.
In this context, meta-heuristic optimization algorithms (Fan and Zhou 2023) have
rapidly developed due to their flexibility and gradient-free mechanisms. They have
become essential tools for solving production efficiency improvement problems. The
flexibility of meta-heuristic optimization algorithms enables them to adapt to diverse
production environments and problem scenarios (Melman and Evsutin 2023). Meta-
heuristic optimization algorithms can search and explore the problem space based
on the characteristics of specific problems to find the best solution or a solution that
comes close to the best one (Abdel-Basset etal. 2023a, b, c). Whether facing prob-
lems such as product design, production planning, resource allocation, or supply chain
management, meta-heuristic optimization algorithms can flexibly adjust and optimize
according to actual situations.
Meanwhile, the meta-heuristic optimization algorithm also has the characteristic
of no gradient mechanism (Liu and Xu 2023), which allows it to deal with problems
without explicit gradient information or continuous derivatives. In many production
environments, obtaining gradient information on the issues through analytical meth-
ods using traditional optimization methods is difficult. The meta-heuristic optimization
algorithm utilizes local knowledge about the problem for optimization through heu-
ristic search and random exploration. In addition to high-dimensional and nonlinear
problems, this gradient-free optimization method is also appropriate for discrete and
constraint-based problems (Boulkroune etal. 2023).
Content courtesy of Springer Nature, terms of use apply. Rights reserved.
Black‑winged kite algorithm: anature‑inspired meta‑heuristic…
1 3
Page 3 of 53 98
1.1 Meta‑heuristic methods
An optimization algorithm based on a heuristic search is called a meta-heuristic optimiza-
tion algorithm (Wang etal. 2023a, b). They usually do not have any special requirements
for the objective function but instead search by simulating intelligent behavior in nature
(Chen etal. 2023) or other phenomena. They are more likely to find a globally optimal
solution with a broader range of applications and a certain probability of escaping the local
optimum. The characteristic of meta-heuristic optimization algorithms is their global solid
search ability and robustness (Xu 2023a, b; Zhao et al. 2023a, b), which can find opti-
mal solutions in large-scale, high-dimensional problems and quickly solve problems that
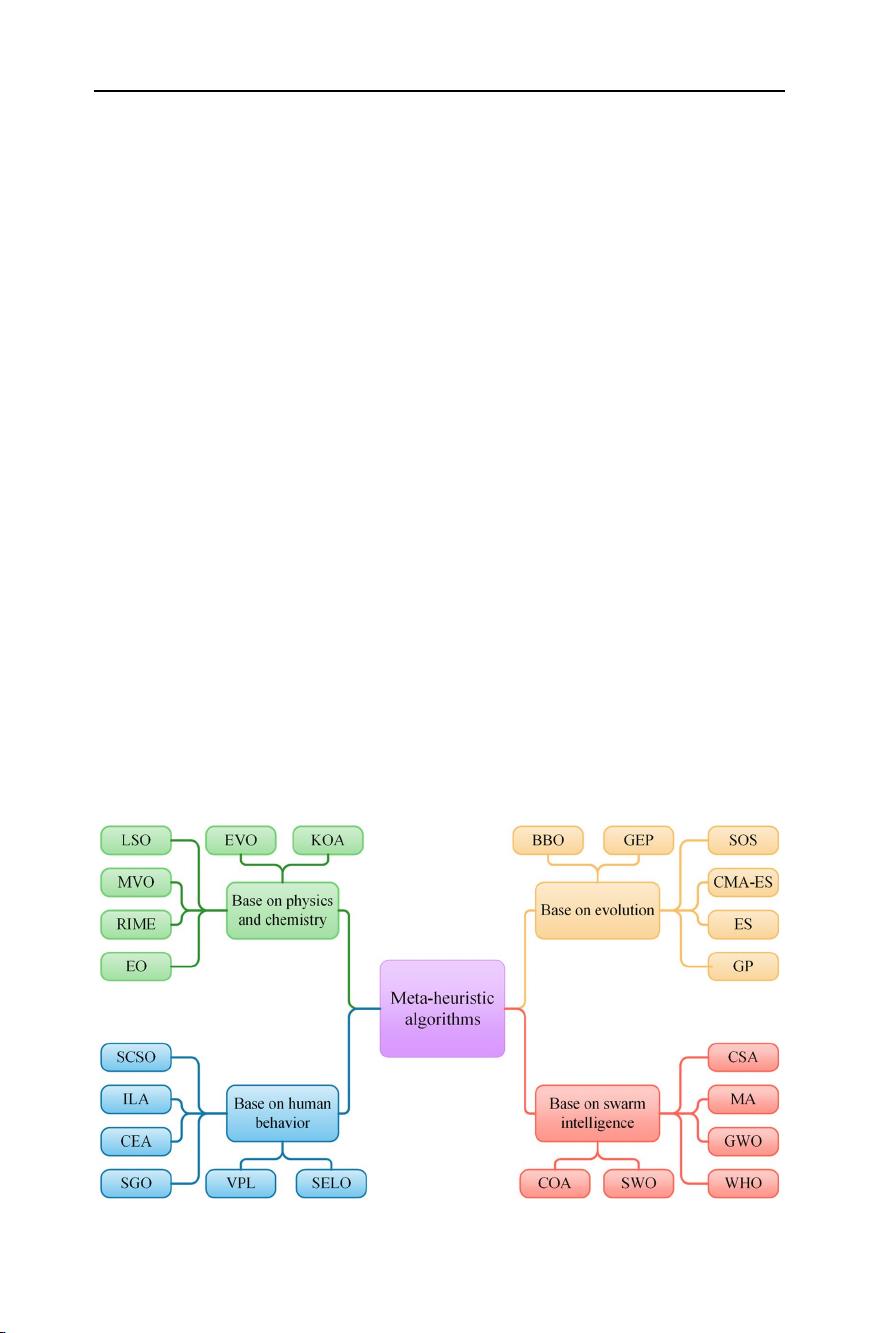
do not exist or have not yet found polynomial time-solving algorithms. The classification
diagram for the meta-heuristic optimization algorithm is shown in Fig.1. Meta-heuristic
algorithms, which combine random algorithms with local algorithms to solve challenging
optimization problems, are inspired by random phenomena in nature (Bingi, etal. 2023).
They can be broadly classified into the following four types based on their various sources
of inspiration:
(1) The algorithm is designed based on the behavioral characteristics of biological popu-
lations. These models simulate organisms’ collective intelligence and collaborative
strategies, enabling the rapid search of problem space and finding global optimal or bet-
ter approximate solutions. Biologically inspired optimization models perform well in
handling continuous and global search problems. Zamani etal. (2022) present a novel
bio-inspired algorithm inspired by starlings’ behaviors during their stunning murmura-
tion named Starling Murmuration Optimizer (SMO) to solve complex and engineering
optimization problems as the most appropriate application of metaheuristic algorithms.
The SMO introduces a dynamic multi-flock construction and three new search strate-
gies: separating, diving, and whirling. Sand Cat Swarm Optimization (Seyyedabbasi
and Kiani 2023) is a meta-heuristic algorithm based on sand cats’ natural behavior. This
algorithm was influenced by sand cats’ capacity to recognize low-frequency noise. Due
Fig. 1 Classification of metaheuristic algorithms
Content courtesy of Springer Nature, terms of use apply. Rights reserved.

J.Wang et al.
1 3
98 Page 4 of 53
to its unique traits, the sand cat can find prey above and below ground. The Squirrel
Search Algorithm (SSA) (Jain etal. 2019) is a single-objective optimization problem-
solving heuristic algorithm based on the feeding habits of wild squirrels. This algorithm
simulates the search strategy of squirrels when searching for food, gradually approach-
ing the optimal solution by continuously adjusting the search position and range. To
achieve the goal of optimization, Aquila Optimizer (AO) (Abualigah etal. 2021) pri-
marily mimics eagles’ behavior while capturing prey. It has strong optimization ability
and fast convergence speed. The inspiration for the Sea Horse Optimizer (SHO) (Zhao
etal. 2023a, b) comes from the hippocampus’s movement, predation, and reproductive
behavior in nature. The foraging and navigational habits of African vultures served as
the basis for the African Vultures Optimization Algorithm (AVOA) (Abdollahzadeh
etal. 2021). Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995) is a
search algorithm developed based on group collaboration by simulating the foraging
behavior of bird flocks. The Chameleon Swarm Algorithm (CSA) (Braik 2021) models
the chameleons’ dynamic foraging behavior in and around trees, deserts, and swamps.
The Mayfly Algorithm (MA) (Zervoudakis and Tsafarakis 2020) is inspired by the
mayflies’ flight behavior and mating process. Wild horses’ lives and behaviors inspired
the Wild Horse Optimizer (WHO) (Naruei and Keynia 2022). Spider Wasp Optimizer
(SWO) (Abdel-Basset etal. 2023b) is proposed based on female spider wasps’ hunting,
nesting, and mating behavior. The Coati Optimization Algorithm (COA) (Dehghani
etal. 2022) is inspired by coatis. The grey wolf’s social structure and hunting strate-
gies served as the basis for the Grey Wolf Optimization (GWO) algorithm (Mirjalili
etal. 2014). The Marine Predators Algorithm (MPA) (Faramarzi etal. 2020a, b) draws
inspiration from the prey-hunting Brownian and Lévy movements of marine predators.
The Ant Lion Optimizer (ALO) (Mirjalili 2015) is modeled after how ants navigate
between their nests and food in their natural behavior. The humpback whales’ bubble
net hunting techniques and natural behavior served as the basis for the Whale Optimi-
zation Algorithm (WOA) (Mirjalili and Lewis 2016). The Dandelion Optimizer (DO)
(Zhao etal. 2022) was proposed to simulate the process of dandelion seeds flying over
long distances by wind. This algorithm considers two main factors, wind speed, and
weather, and introduces Brownian motion and Levi flight to describe the seed’s motion
trajectory. Golden Jackal Optimization (GJO) (Chopra and Ansari 2022) is inspired by
the cooperative hunting behavior of golden jackals in nature.
(2) Algorithms abstracted from human behavior or social phenomena. These models have
strong learning ability and adaptability and have demonstrated excellent performance
in image recognition and natural language processing fields. The Volleyball Premier
League (VPL) (Moghdani and Salimifard 2018) is inspired by the rivalry and inter-
action between various volleyball teams throughout the season. The social learning
behavior of humans arranged in families in the social environment is the basis for
the Social Evolution and Learning Optimization (SELO) (Kumar etal. 2018) algo-
rithm. The inspiration for Social Group Optimization (SGO) (Satapathy and Naik
2016) comes from social group learning. The inspiration for the Cultural Revolution
Algorithm (CEA) (Kuo and Lin 2013) comes from the process of social transforma-
tion. Hunter Prey Optimization (HPO) (Naruei etal. 2021) is inspired by the process
of animal hunting. The inspiration for the IbI Logic Algorithm (Azizi etal.) (Mirrashid
and Naderpour 2023) comes from thinking about brain logic.
(3) Inspired by genetic evolution algorithms. These models can handle discrete and multi-
objective optimization problems and have strong robustness and global search ability
for complex issues. Gene Expression Programming (GEP) (Sharma 2015) aims to use
Content courtesy of Springer Nature, terms of use apply. Rights reserved.

Black‑winged kite algorithm: anature‑inspired meta‑heuristic…
1 3
Page 5 of 53 98
gene expression programming to simulate the mathematical expression relationship
between data points in a set of data points based on the laws of genetic inheritance, the
idea of natural selection, survival of the fittest, and elimination of the best. The popula-
tion is constantly evolving to find the most suitable chromosome. The processes of how
species move from one island to another, how new species appear, and how species go
extinct are the inspirations for Biogeography-Based Optimization (BBO) (Simon 2008)
and Covariance Matrix Adaptation Evolution Strategy (CMA-ES) (Hansen and Kern
2004). The inspiration for Symbiotic Organisms Search (SOS) (Cheng and Prayogo
2014) comes from symbiotic phenomena in biology. The inspiration for Evolution
Strategies (ES) (Beyer and Schwefel 2002) comes from biological evolution. Genetic
programming is inspired by natural selection (GP) (Koza 1992).
(4) Algorithms abstracted from physical properties or chemical reactions as inspiration.
These models can jump between multiple local optimal solutions and find global opti-
mal solutions by simulating the characteristics of physical phenomena and optimiz-
ing search strategies. The Kepler Optimization Algorithm (KOA) (Abdel-Basset etal.
2023a, b, c) is a physics-based meta-heuristic algorithm that predicts the position and
motion of planets at any given time by Kepler’s laws of planetary motion. Energy Val-
ley Optimizer (EVO) (Azizi etal. 2023) is a brand-new meta-heuristic algorithm that
draws inspiration from physical theory’s various particle decay modes and stability
laws. Light Spectrum Optimizer (LSO) (Abdel-Basset etal. 2022) is a new physics-
inspired meta-heuristic algorithm that generates meteorological phenomena of colored
rainbow spectra inspired by the dispersion of light at different angles when passing
through raindrops. Rime Optimization Algorithm (RIME) (Su etal. 2023), which
constructs a soft time search strategy and a hard time puncture mechanism, simulates
ice’s soft time and hard time growth processes and achieves exploration and develop-
ment behavior in optimization methods. Multi-verse Optimization (MVO) (Mirjalili
etal. 2016) is inspired by the fact that the universe has an expansion rate, utilizing the
principle that white holes have higher and black holes have a lower expansion rate. The
particles in the universe search through the principle of transferring from white spots
to black holes through wormholes. The control volume mass balance model, used to
estimate dynamic and equilibrium states, is the primary source of inspiration for the
Equilibrium Optimizer (EO) (Faramarzi etal. 2020a, b).
1.2 Related work
In this section, we discussed some recent work.
Banaie-Dezfouli etal. (2023) introduce an improved binary GWO algorithm called the
extreme value-based GWO (BE-GWO) algorithm. This algorithm proposes a new cosine
transfer function (CTF) to convert continuous GWO into binary form. Then, it introduces
an extreme value (Ex) search strategy to improve the efficiency of converting binary solu-
tions. Nama etal. (2023) propose a new ensemble algorithm called e-mPSOBSA with the
reformed Backtracking Search Algorithm (BSA) and PSO. Chakraborty etal. (2022) sug-
gest an enhanced SOS algorithm called nwSOS to resolve higher dimensional optimiza-
tion issues. Nama and Saha (2022) introduce an improved BSA (ImBSA) based on multi-
group methods and modified control parameter settings to understand the collection of
various mutation strategies. Nama (2021) proposes an improved form of SOS to establish
an increasingly stable balance between discovery and activity cores. This technology uses
three unique programs: adjusting benefit factors, changing parasitic stages, and searching
Content courtesy of Springer Nature, terms of use apply. Rights reserved.

















