2006年全国研究生数学建模竞赛优秀论文选-A题 02.pdf

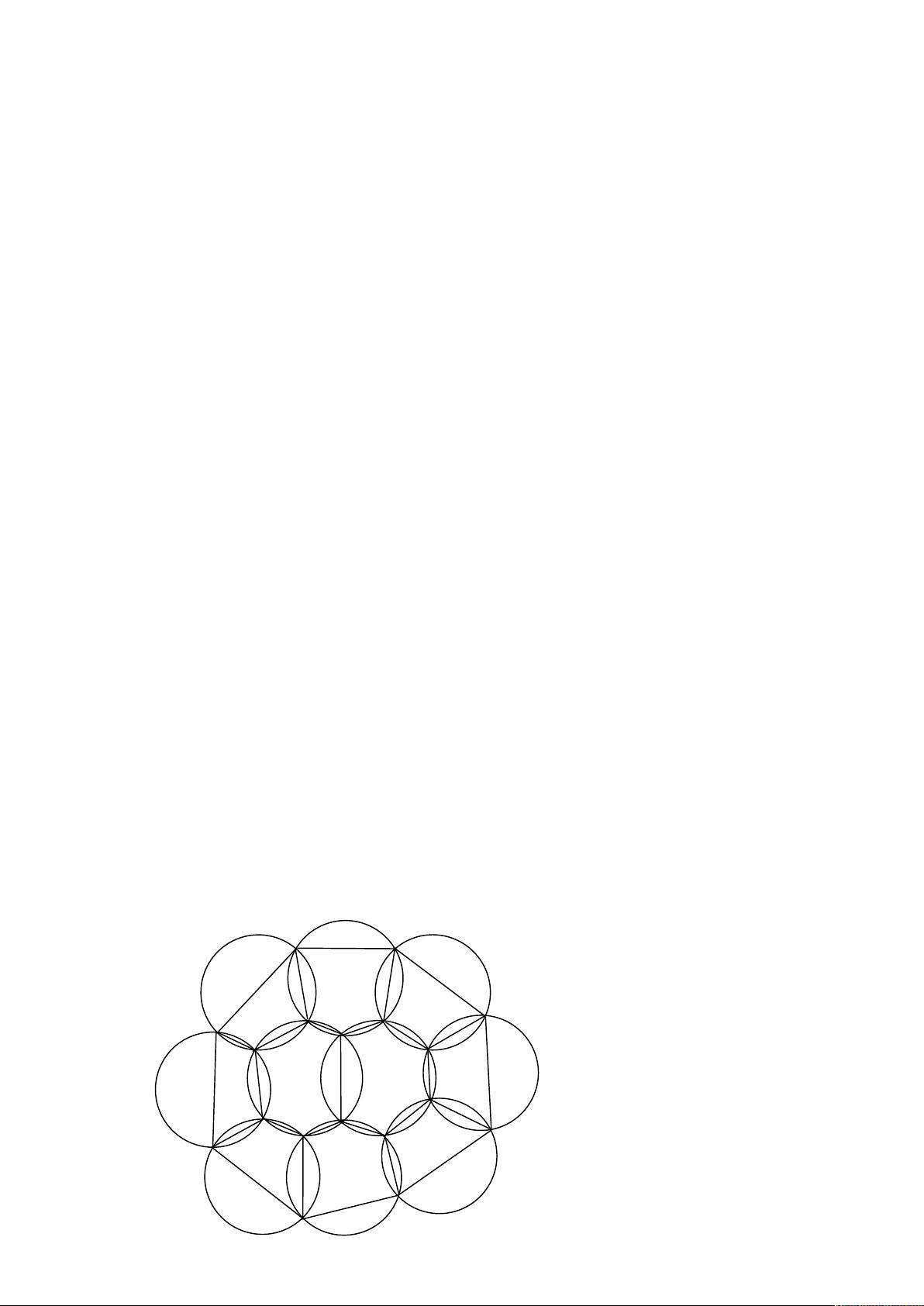
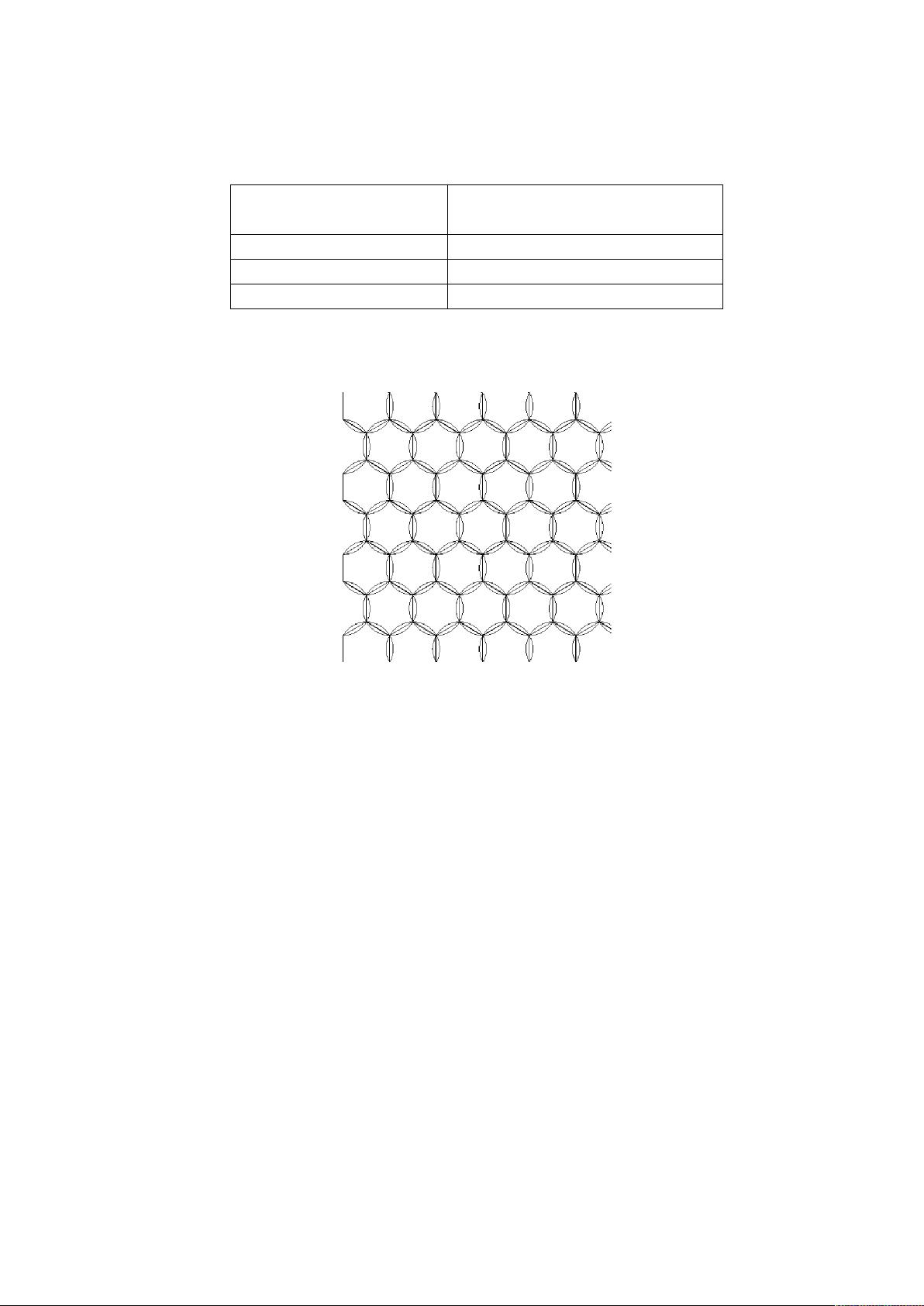
### 2006年全国研究生数学建模竞赛优秀论文选-A题 02.pdf #### 关键知识点解析 本文是一篇关于Ad Hoc网络在特定区域内构建覆盖区及其信道分配优化方案的研究报告，主要关注如何在满足一定条件的情况下实现网络的最佳布局。通过建立数学模型并采用近似算法来解决NP完全问题，最终评估了网络的抗毁性。 ### 一、平面的圆覆盖问题 #### 1.1 圆个数的最小值 ##### 1.1.1 最优化模型 目标是寻找能够完全覆盖指定正方形区域（1000×1000）的圆的最小数量，同时确保任意两个相邻圆之间的公共面积不少于一个圆面积的5%。这一问题可以被形式化为以下数学模型： \[ \begin{aligned} & \text{minimize } & & n \\ & \text{subject to} & & \bigcup_{c \in C} c \supseteq P, \\ & & & \forall (c_i, c_j) \text{ adjacent, } |c_i \cap c_j| \geq 0.05 |c_i|, \\ & & & n = |C|, \end{aligned} \] 其中 \(C = \{c_1, c_2, \ldots, c_n\}\) 表示一组圆，\(P\) 是需要被覆盖的平面区域，\(n\) 是圆的数量，而 \(|c|\) 表示圆 \(c\) 的面积。这里的约束条件意味着所有的圆必须共同覆盖整个平面区域，并且每对相邻的圆之间必须有一定的重叠面积。 #### 1.2 优化算法选择 由于直接求解该问题属于NP完全问题，因此需要采用近似算法来找到较为满意的解决方案。文章中提到了几种方法，包括： - **分析方法**：针对问题1中的圆覆盖问题，采用分析法寻找解决方案。 - **遗传算法**：用于解决问题2和问题3中的优化问题，特别是当需要考虑额外约束条件（如湖泊的存在）时。 ### 二、信道分配问题 #### 2.1 平面图着色问题 信道分配问题可以转换为平面图着色问题，即如何将信道（颜色）分配给平面图中的每个节点（圆），以确保相邻节点的颜色不同。这是一个经典的图论问题，可以通过已知的图着色算法来解决，例如贪心算法或改进的回溯算法等。 ### 三、网络的抗毁性评估 #### 3.1 抗毁性的度量 为了评估网络的抗毁性，文章提出了基于图的连通性来定义抗毁性的度量指标。具体来说，可以通过计算在随机移除部分节点后网络仍然保持连通的概率来量化其抗毁能力。这一过程通常采用蒙特卡罗模拟方法进行。 #### 3.2 蒙特卡罗模拟法 通过模拟随机移除节点的情况，并统计网络仍能保持连通的比例，可以近似地估计出网络的抗毁性。这种方法不仅直观而且易于实现，非常适合于解决此类复杂系统的问题。 ### 四、问题总结与讨论 #### 4.1 总结 本文围绕Ad Hoc网络的覆盖和信道分配问题展开了深入研究，通过对多个子问题的数学建模和求解，不仅找到了有效的优化方案，还评估了网络的抗毁性。这些研究成果对于实际部署Ad Hoc网络具有重要的指导意义。 #### 4.2 讨论 - **算法适用性**：文章中提到的算法（尤其是遗传算法）在处理复杂优化问题时表现出较好的效果，但在实际应用中还需要考虑计算资源和时间成本。 - **扩展性**：尽管研究中提出的模型和方法适用于特定场景，但它们也为解决其他类型的网络覆盖问题提供了有益的思路。 - **未来研究方向**：进一步探索更高效的优化算法，提高求解速度；结合实际情况考虑更多约束条件，使模型更加贴近实际应用场景。 这篇论文通过一系列详尽的数学模型和算法设计，为Ad Hoc网络的覆盖优化和抗毁性评估提供了有价值的理论基础和技术支持。