圆锥曲线中的范围问题.pdf

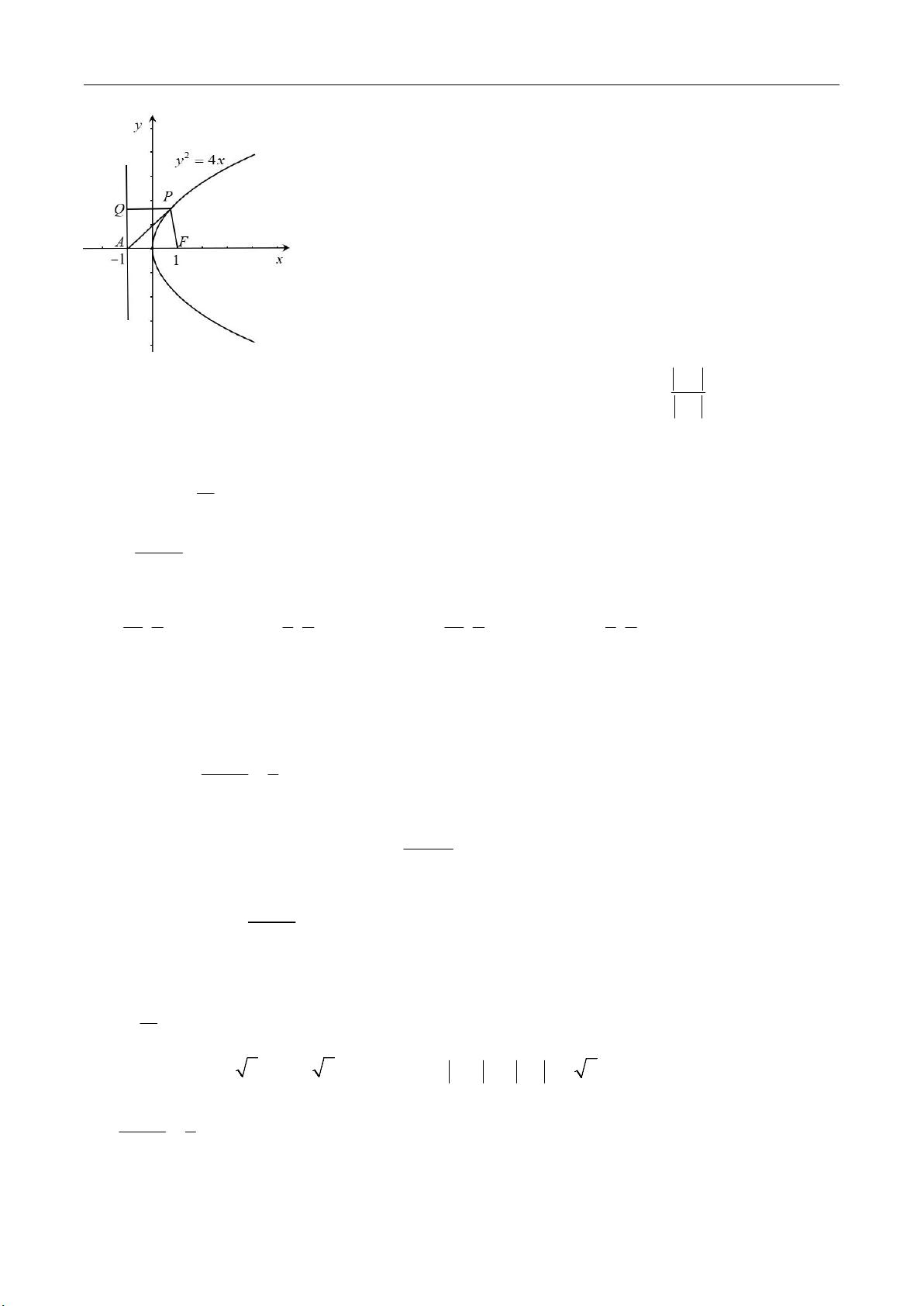
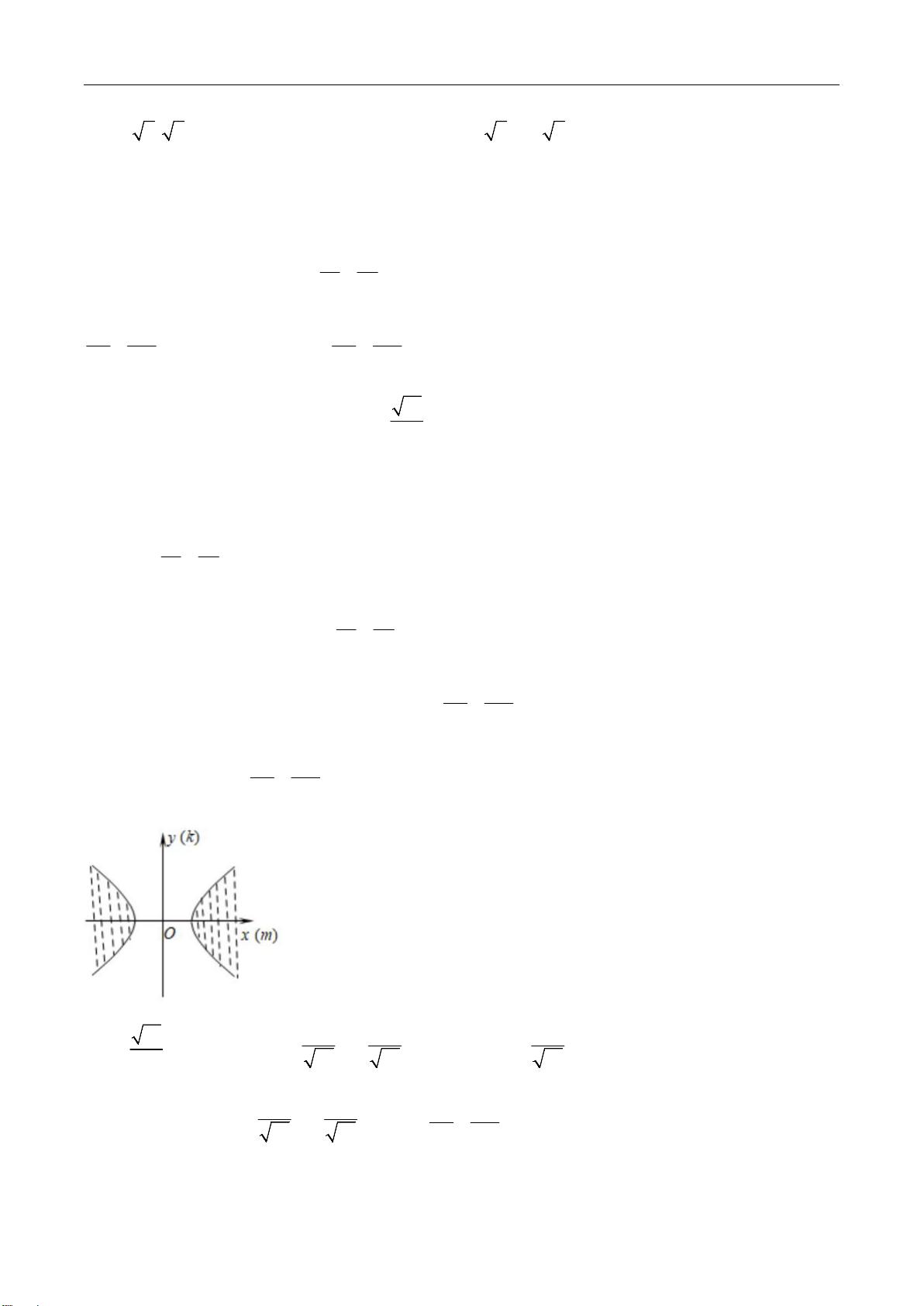
一、抛物线的范围问题 在抛物线的范围问题中，首先需要掌握抛物线的基本定义及其性质。对于一个标准的抛物线方程 \(y^2=4ax\)，焦点位于点 \(F(a,0)\)，而准线的方程为 \(x=-a\)。题目中提到的抛物线方程为 \(y^2=x\)，可以视为 \(y^2=4(\frac{1}{4})x\)，即 \(a=\frac{1}{4}\)。焦点 \(F\) 为 \((\frac{1}{4}, 0)\)。 当点 \(P\) 在抛物线上运动时，若 \(PF\) 的值（从 \(P\) 到焦点 \(F\) 的距离）最小，则 \(P\) 点与焦点 \(F\) 位于抛物线的对称轴上，即 \(x\) 轴上。此时 \(PF\) 实际上就是 \(PA\)（从 \(P\) 到点 \(A(1,0)\)）的长度。为了求得 \(PA\) 的最小值，需要通过使 \(PAF\) 的夹角最大来实现，意味着直线 \(PA\) 斜率的绝对值要尽可能大。 通过设定直线 \(PA\) 的方程为 \(y=kx+b\)，其中 \(b\) 由于点 \(A\) 在 \(x\) 轴上，因此为 \(0\)。然后将直线 \(PA\) 的方程与抛物线方程联立，即可求得满足条件的 \(P\) 点坐标。最后通过距离公式计算 \(PF\) 的长度，从而得出 \(PF\) 的最小值。 二、椭圆的范围问题 对于椭圆范围问题，首先需要了解椭圆的标准方程和相关性质。已知的椭圆方程为 \(\frac{x^2}{4}+\frac{y^2}{2}=1\)，其左焦点 \(F\) 的坐标为 \((-1,0)\)。直线 \(l\) 过椭圆左焦点 \(F\) 并与椭圆相交于 \(A\) 和 \(B\) 两点，其 \(AB\) 中垂线的交点 \(M\) 与 \(x\) 轴的距离有确定的范围。 通过将直线 \(l\) 的方程与椭圆的方程联立，可以消元并化简求得交点 \(A\) 和 \(B\) 的坐标。然后利用弦长公式和两点间距离公式，结合韦达定理，可以求得 \(A\) 和 \(B\) 的中点坐标 \(D\)，进而得到 \(AB\) 的中垂线方程。通过令中垂线方程中的 \(y\) 为 \(0\)，可以求得 \(M\) 点的横坐标，即 \(M\) 点与 \(x\) 轴的交点坐标，从而得出 \(|FM|\) 和 \(|AB|\) 的值，最终求得 \(|FM|/|AB|^2\) 的取值范围。 三、圆与椭圆的范围问题 本部分问题涉及到圆和椭圆上任意两点间的距离问题。已知点 \(P\) 在圆上，而点 \(Q\) 在椭圆上。圆的方程为 \((x-0)^2+(y-3)^2=1^2\)，其中圆心 \(C\) 为 \((0,3)\)，半径 \(r=1\)。椭圆的方程为 \(\frac{x^2}{2^2}+\frac{y^2}{5^2}=1\)，即 \(\frac{x^2}{4}+\frac{y^2}{25}=1\)。 为了求得 \(P\) 和 \(Q\) 两点间的最大距离，我们需要先设定椭圆上任意一点的坐标 \(Q\)。由于椭圆的参数方程可设为 \((2\cos\theta, 5\sin\theta)\)，其中 \(\theta\) 为参数，取值范围在 \(0\) 到 \(2\pi\) 之间。 最大距离是在椭圆的长轴方向取得，即当 \(\theta = \pi/2\) 时，此时 \(Q\) 点的坐标为 \((0,5)\)。因此，最大距离为椭圆上 \(Q\) 点到圆心 \(C\) 的距离加上圆的半径，即 \(QC+r\)。通过三角函数和代入参数 \(\theta\)，我们可以得出 \(P\) 和 \(Q\) 两点间距离的最大值为 \(2\sqrt{17}+1\)。 总结来说，圆锥曲线的范围问题主要是通过数学推导和计算，利用圆锥曲线的性质，结合坐标几何和三角学的方法求解。掌握这些基本的数学工具对于解决此类问题至关重要。同时，需要注意，在联立椭圆和直线方程时，要检验判别式确保方程有实数解，才能进一步求解。