
Universidad de Puerto Rico
Recinto de Mayagüez
Tarea LPC
Christian Vázquez
Pedro Colon

Cepstral features can be related to LP features. Describe the relationship between the two.
The relationship is that we can transform the LP features (coefficients) into the Cepstral features
(coefficients). This relationship can be seen with the formula:
And
Where a
k
is the Kth LPC. These are recursive formulas that use previous values to find new
ones.
Works Cited
Tokuda, Keiichi, Takao Kobayashi, and Satoshi Imai. "Recursive Calculation of Mel-Cepstrum
from LP Coefficients." TOKUDA, LEE and NANKAKU LABORATORY. 1 Apr. 1994.
Web. 17 Nov. 2014. <http://www.sp.nitech.ac.jp/~tokuda/tips/mgceptr_sa2.pdf>.
"5.3 Linear Prediction Analysis." 5.3 Linear Prediction Analysis. Web. 17 Nov. 2014.
<http://www.ee.columbia.edu/ln/LabROSA/doc/HTKBook21/node53.html>.
Atal, B. S. "Effectiveness of the Linear Prediction Characteristics of the Speech Wave for
Automatic Speaker Identification and Verification." 2 Jan. 1974. Web. 17 Nov. 2014.
<http://www.ee.columbia.edu/~dpwe/papers/Atal74-lpc.pdf>.
"L9: Cepstral Analysis." Web. 17 Nov. 2014.
<http://research.cs.tamu.edu/prism/lectures/sp/l9.pdf>.
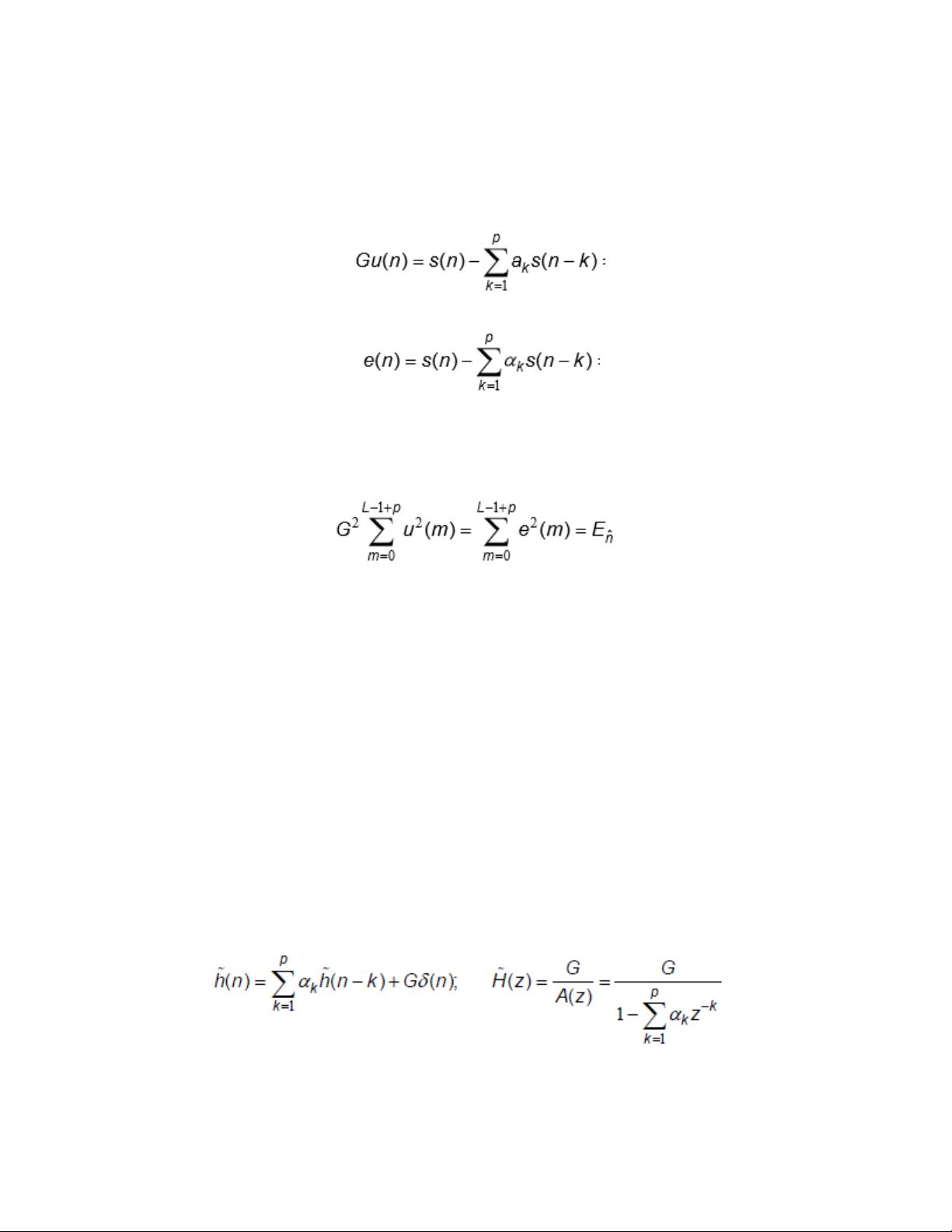
The model for linear prediction includes a gain G on the input excitation. Describe how this gain
can be computed.
The model gain, G, to be determined by matching the signal energy with the energy of the
linearly predicted samples.
At first glance, the following equation could be used:
The previous equation would be equaled to the equation for the prediction error:
In the ideal case a
k
=α
k
, but since this would hardly ever happen, the approximation is not exactly
valid. So, instead we can use energy the matching criterion (energy in error signal=energy in
excitation). This can be seen in the following equation:
However, to solve for G, we would need to work with the voiced and unvoiced parts of speech.
We would make the assumption that:
For voiced:
U(n) = δ(n) :
� L order of a single pitch period
� predictor order p large enough to model glottal pulse shape
� vocal tract IR
� radiation
For unvoiced:
U(n)
� zero mean
� unity variance
� stationary white noise process
Solving for the voiced gain:
The excitation is G δ(n) with an output of h(n) because it is the impulse response of the system.
This has an autocorrelation R
~
(m) (of the impulse response) that satisfies:

Since R
~
(m) has the same equation as:
Which is the short term auto correlation of the signal,
We can say that:
Since the total energies in the signal (R(0)) and the impulse response (R
~
(0)) must be equal, the
constant c must be 1, and
Solving for the unvoiced gain:
The input of the system is white noise with zero mean and unity variance:
If we put in an input Gu(n) and name the output g
~
(n):
Since the autocorrelation function for the output is the convolution of the autocorrelation function
of the impulse response with the autocorrelation of the white noise input:
Where R
~
(m) is the autocorrelation of the output g
~
(n). We can also see that:

















