随机数 平均分布 高斯分布

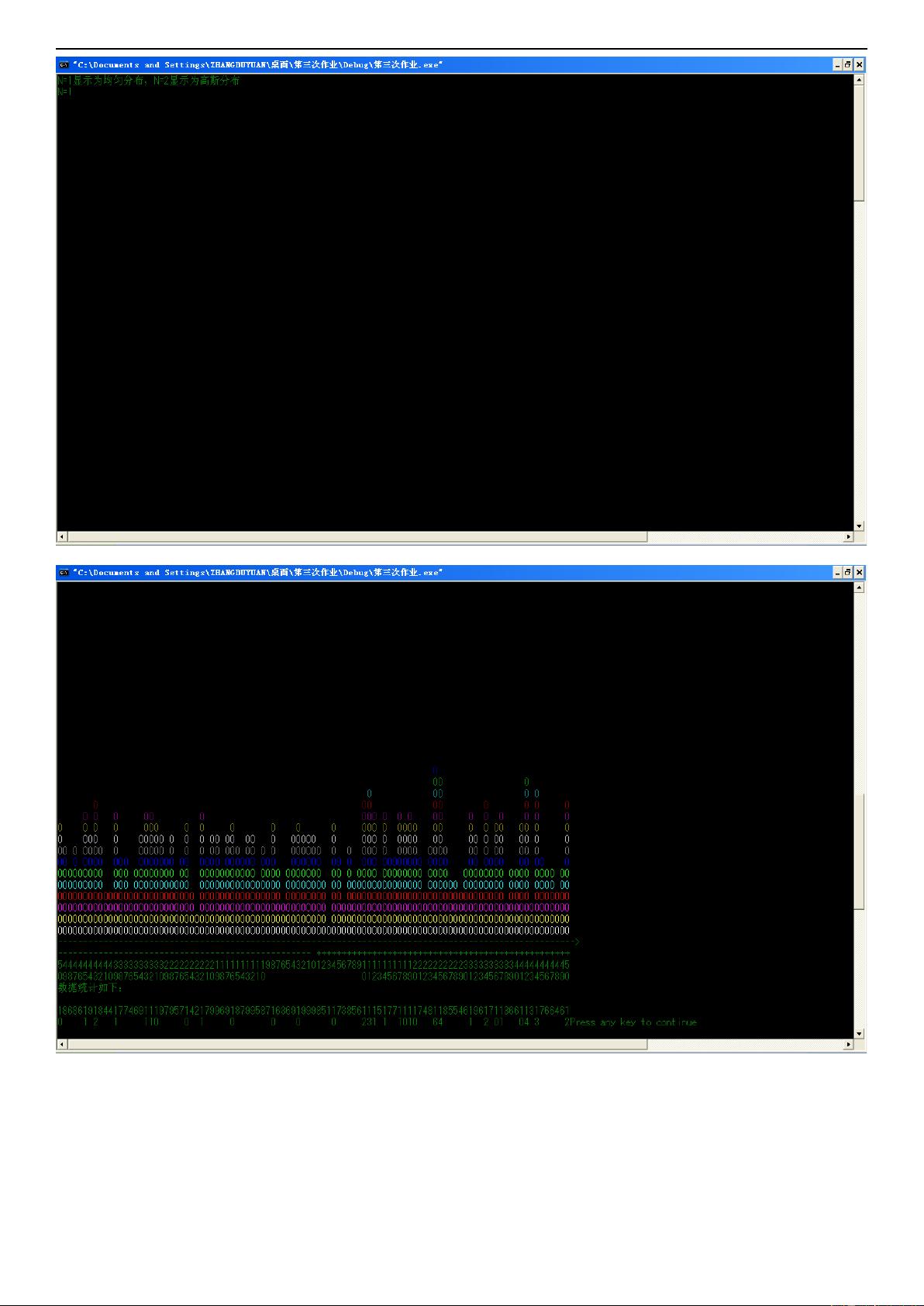
根据给定的文件信息，我们可以总结出以下关于随机数、平均分布与高斯分布的关键知识点： ### 随机数生成原理与应用 在计算机科学中，随机数生成是通过算法来模拟真正的随机性，虽然计算机生成的随机数通常被称为伪随机数，因为它们是由确定性的算法产生的，但在大多数情况下，这些伪随机数足以满足实际需求，如在统计分析、密码学、游戏开发等领域。 #### 均匀分布与高斯分布 - **均匀分布**：在一定范围内，每个数值出现的概率都是相等的。例如，在0到1之间生成随机数时，任何介于0到1之间的数字都有相同的概率被选中。 - **高斯分布**（也称为正态分布）：是一种连续概率分布，其特点是具有钟形曲线，数据集中在平均值附近，离平均值越远的数据出现的概率越低。高斯分布由两个参数决定：均值（μ）和标准差（σ）。均值决定了分布的中心位置，而标准差则决定了数据分布的宽度。 ### 实验目的 实验旨在通过编程实现两种随机数分布的可视化——均匀分布和高斯分布。通过设置不同的参数（N=1表示均匀分布，N=2表示高斯分布），观察并理解这两种分布的特性和差异。 ### C++代码解析 该实验使用C++语言编写，涉及了多个库函数，包括`windows.h`用于控制台颜色和位置，`stdlib.h`和`time.h`用于随机数生成，以及`iostream.h`用于输入输出操作。具体代码实现了如下功能： 1. **随机数生成与控制台输出**：通过`srand`函数初始化随机数种子，使用`rand`函数生成随机数，并利用`SetConsoleCursorPosition`和`SetConsoleTextAttribute`函数在控制台上动态显示随机数的分布情况。 2. **图形化展示**：代码不仅生成随机数，还通过控制台字符的位置和颜色变化，直观地展示了随机数的分布形态，即均匀分布和高斯分布的图形表现。 ### 实验结果 实验结果表明，当N取值为1时，控制台显示出均匀分布的特征，所有数值在指定范围内均匀分布；而当N取值为2时，则显示出高斯分布的特性，数值集中于均值附近，两边逐渐减少，形成典型的钟形曲线。 ### 结论与拓展 通过本次实验，我们不仅了解了随机数生成的基本原理，还深入探索了两种重要的随机数分布类型——均匀分布与高斯分布，并通过编程实践加深了对这些概念的理解。此外，实验还展示了如何在控制台上以图形方式呈现这些分布，提供了一种直观的教学和学习方法。 对于有兴趣进一步学习随机数生成及其在不同领域应用的学生而言，掌握C++中的随机数生成技术是非常有价值的。未来可以尝试将这些理论应用到更复杂的项目中，如蒙特卡洛模拟、数据加密或游戏开发，以加深对随机性的理解和应用能力。