随机波动kim（1998）论文资源-CSDN文库

贝叶斯

随机波动

需积分: 9 55 浏览量 2018-12-23 22:57:54 上传评论收藏 4.8MB PDF 举报

资源推荐

资源详情

资源评论

Review of Economic Studies (1998) 65, 361-393

0034-6527/98/00170361$02.00

Stochastic Volatility: Likelihood

Inference and Comparison with

ARCH

Models

SANGJOON

KIM

Salomon Brothers Asia Limited

NEIL SHEPHARD

Nuffield College, Oxford

and

SIDDHARTHA CHIB

Washington University, St. Louis

First version received December 1994; final version accepted August 1997 (Eds.)

In this paper, Markov chain Monte Carlo sampling methods are exploited to provide a

unified, practical likelihood-based framework for the analysis of stochastic volatility models. A

highly effective method is developed that samples all the unobserved volatilities at once using an

approximating offset mixture model, followed by an importance reweighting procedure. This

approach is compared with several alternative methods using real data. The paper also develops

simulation-based methods for filtering, likelihood evaluation and model failure diagnostics. The

issue of model choice using non-nested likelihood ratios and Bayes factors is also investigated.

These methods are used to compare the fit of stochastic volatility and GARCH models. All the

procedures are illustrated in detail.

1. INTRODUCTION

The variance of returns on assets tends to change over time. One way of modelling this

feature of the data is to let the conditional variance be a function of the squares of

previous observations and past variances. This leads to the autoregressive conditional

heteroscedasticity (ARCH) based models developed by Engle (1982) and surveyed in

Bollerslev, Engle and Nelson (1994).

An alternative to the

ARCH

framework is a model in which the variance is specified

to follow some latent stochastic process. Such models, referred to as stochastic volatility

(SV) models, appear in the theoretical finance literature on option pricing (see, for example,

Hull and White (1987) in their work generalizing the

Black-Scholes option pricing formula

to allow for stochastic volatility). Empirical versions of the SVmodel are typically formula-

ted in discrete time. The canonical model in this class for regularly spaced data is



(1)

361

at University of Texas at Austin on October 5, 2011restud.oxfordjournals.orgDownloaded from

362

REVIEW OF ECONOMIC STUDIES

where

YI is the mean corrected return on holding the asset at time t, h, is the log volatility

at time

t which is assumed to follow a stationary process

c/J

I< I) with h, drawn from

the stationary distribution,

CI and

1]1

are uncorrelated standard normal white noise shocks

and

%(.,.)is the normal distribution. The parameter

or exp

(JJ

/2)

plays the role

the constant scaling factor and can be thought

as the modal instantaneous volatility,

c/J

as the persistence in the volatility, and aT/the volatility of the log-volatility.

For

indenti-

fiability reasons either

must be set to one or

to zero. We show later that the param-

eterization with

equal to one in preferable and so we shall leave

unrestricted when

we estimate the model but report results for

= exp

(JJ

/2)

as this parameter has more

economic interpretation.

This model has been used as an approximation to the stochastic volatility diffusion

by Hull and White (1987) and Chesney and Scott (1989). Its basic econometric properties

are discussed in Taylor (1986), the review papers by Taylor (1994), Shephard (1996) and

Ghysels, Harvey and Renault (1996) and the paper by Jacquier, Polson and Rossi (1994).

These papers also review the existing literature on the estimation of SV models.

In this paper we make advances in a number of different directions and provide the

first complete Markov chain Monte Carlo simulation-based analysis

the SV model

(I)

that covers efficient methods for Bayesian inference, likelihood evaluation, computation

filtered volatility estimates, diagnostics for model failure, and computation

statistics

for comparing non-nested volatility models. Our study reports on several interesting find-

ings. We consider a very simple Bayesian method for estimating the SV model (based on

one-at-a-time updating

the volatilities). This sampler is shown to be quite inefficient

from a simulation perspective. An improved (multi-move) method that relies on an offset

mixture

normals approximation to a log-chi-square distribution coupled with an import-

ance reweighting procedure is shown to be strikingly more effective. Additional refinements

of the latter method are developed to reduce the number

blocks in the Markov chain

sampling. We report on useful plots and diagnostics for detecting model failure in a

dynamic (filtering) context. The paper also develops formal tools for comparing the basic

SVand

Gaussian and t-GARCH models. We find that the simple SV model typically fits

the data as well as more heavily parameterized

GARCH

models. Finally, we consider a

number

extensions

the SV model that can be fitted using our methodology.

The outline

this paper is as follows. Section 2 contains preliminaries. Section 3

details the new algorithms for fitting the SV model. Section 4 contains methods for simula-

tion-based filtering, diagnostics and likelihood evaluations. The issue

comparing the

SV and

GARCH

models is considered in Section 5. Section 6 provides extensions while

Section 7 concludes. A description of software for fitting these models that is available

through the internet is provided in Section 8. Two algorithms used in the paper are

provided in the Appendix.

2. PRELIMINARIES

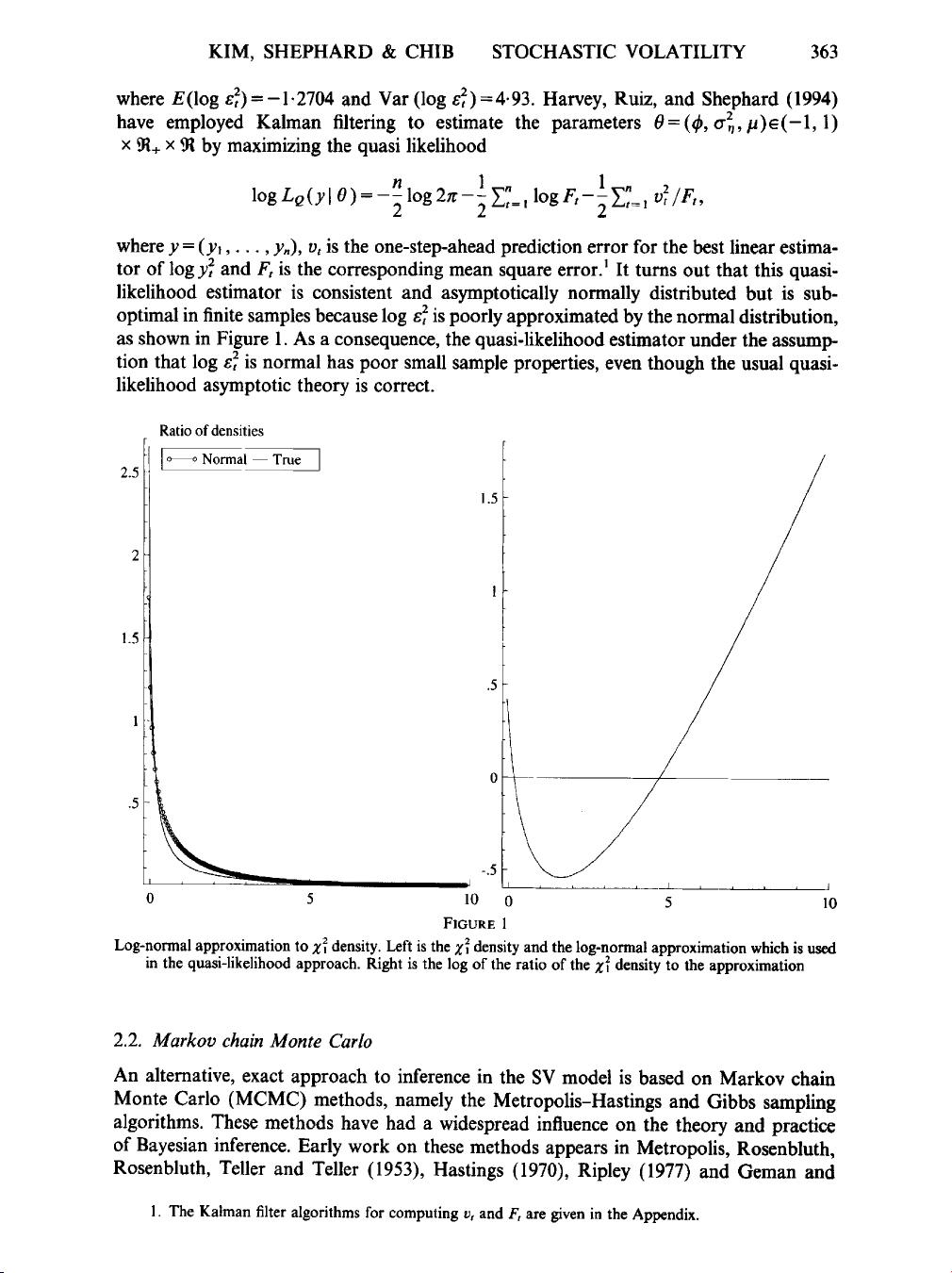
2.1. Quasi-likelihood method

A key feature

the basic SV model in (1) is that it can be transformed into a linear

model by taking the logarithm of the squares of observations



log



(2)

at University of Texas at Austin on October 5, 2011restud.oxfordjournals.orgDownloaded from

364

REVIEW

ECONOMIC STUDIES

Geman (1984) while some

the more recent developments, spurred by Tanner and Wong

(1987) and Gelfand and Smith (1990), are included in Chib and Greenberg (1996), Gilks,

Richardson and Spiegelhalter (1996) and Tanner (1996, Ch. 6). Chib and Greenberg

(1995) provide a detailed exposition of the Metropolis-Hastings algorithm and include a

derivation

the algorithm from the logic of reversibility.

The idea behind MCMC methods is to produce variates from a given multivariate

density (the posterior density in Bayesian applications) by repeatedly sampling a Markov

chain whose invariant distribution is the target density of interest. There are typically

many different ways of constructing a Markov chain with this property and one goal of

this paper is to isolate those that are simulation-efficient in the context of SV models. In

our problem, one key issue is that the likelihood function

f(y

()

= Jf

Ih, () f (h I

()dh

is intractable. This precludes the direct analysis of the posterior density

n«()

by MCMC

methods. This problem can be overcome by focusing instead on the density

n«(),

hIY),

where h = (hI,

...

)

is the vector of n latent volatilities. Markov chain Monte Carlo

procedures can be developed to sample this density without computation of the likelihood

functionf(y

I(). It should be kept in mind that sample variates from a MCMC algorithm

are a high-dimensional (correlated) sample from the target density of interest. These draws

can be used as the basis for making inferences by appealing to suitable ergodic theorems for

Markov chains.

For

example, posterior moments and marginal densities can be estimated

(simulation consistently) by averaging the relevant function of interest over the sampled

variates. The posterior mean

() is simply estimated by the sample mean of the simulated

() values. These estimates can be made arbitrarily accurate by increasing the simulation

sample size. The accuracy of the resulting estimates (the so called numerical standard

error) can be assessed by standard time series methods that correct for the serial correlation

in the draws. The serial correlation can be quite high for badly behaved algorithms.

2.2.1. An initial Gibbs sampling algorithm for the SV model

For

the problem

simulating a multivariate density n( 'II I y), the Gibbs sampler is defined

by a blocking scheme

'II =('III,

...

, 'IId) and the associated full conditional distributions

'IIi I 'II

\i,

where 'II \i denotes 'II excluding the block 'IIi' The algorithm proceeds by sampling

each block from the full conditional distributions where the most recent values

the

conditioning blocks are used in the simulation. One cycle

the algorithm is called a

sweep or a scan. Under regularity conditions, as the sampler is repeatedly swept, the draws

from the sampler converge to draws from the target density at a geometric rate.

For

the

SV model the

w vector becomes (h,

().

To sample v from the posterior density, one

possibility (suggested by Jacquier, Polson and Rossi (1994) and Shephard (1993» is to

update each of the elements of the

'II vector one at a time.

1. Initialize

hand

().

2. Sample

h, from htl

h\t,

y, (),

...

, n.

3. Sample



Iy, h,

4>,

{3.

4. Sample

Ih, u,

{3,



5. Sample jJ Ih,

4>,



6. Goto 2.

Cycling through 2 to 5 is a complete sweep of this (single move) sampler. The Gibbs

sampler will require us to perform many thousands of sweeps to generate samples from

(),h\y.

at University of Texas at Austin on October 5, 2011restud.oxfordjournals.orgDownloaded from

KIM,

SHEPHARD

& CHIB STOCHASTIC VOLATILITY

365

The most difficult part

this sampler is to effectively sample from h,Ih\t' Yt, 8 as

this operation has to be carried out

n times for each sweep. However,

...

, n.

We sample this density by developing a simple accept/reject procedure.' Let fN(t1

a, b)

denote the normal density function with mean a and variance b.

can be shown (ignoring

end conditions to save space) that

f(h

Ih\t, 8) =

f(h

h.;

8) = fN(h



, v

where

-,-l/J...:-{

(_h

t_-

-......;..Jl_)_+--::-(h_t+_I_-_Jl.....:...)

}

- r: (I + l/J2)

and

Next we note that exp (

-h

)

is a convex function and can be bounded by a function linear

in ht. Let

10gf(Ytlhh

8)=const+logf*(Yt,h

8). Then

*-1 Y;{

logf

(Yt, ht, 8) -

- exp





{exp



-h,

exp



=logg*(Yt,

h., 8,



Hence

The terms on the right-hand side can be combined and shown to be proportional to

fN(htIJlt, v

)

where

* V 2 h*

Jlt=h

[Yt

exp(-

d-I].

(3)

2. Other MCMC algorithms for simulating from

h,lh'-hh'+I'Y';

(J have been given in the literature by

Shephard (1993), Jacquier, Polson and Rossi (1994), Shephard and Kim (1994), Geweke (1994) and Shephard

and Pitt (1997). The closest to our suggestion is Geweke (1994) who also bounded

log/*,

but by

-0·5h,.

This

suffers from the property

having a high rejection rate for slightly unusual observations (for example, 0·9 for

Iy, I/

exp (h,

/2)

> 3). Shephard and Pitt (1997), on the other hand, used a quadratic expansion of

logj"

about

hi. This increases the generality of the procedure but it involves a Metropolis rejection step and so is more

involved. Shephard (1993) approximated

by a normal distribution with the same moments as log

e:.

Geweke (1994) and Shephard and Kim (1994) independently suggested the use of the Gilks and Wild

(1992) procedure for sampling from log concave densities such as

10g/(h,lh

(J, y). This is generalizable to

non-log-concave densities using the Gilks, Best and Tan (1995) sampler. Typically these routines need about 10

to 12 evaluations of 10g/(h,1

h., (J, y) to draw a single random variable. Hence they are about 10 times less

efficient than the simple accept/reject algorithm given above.

Jacquier, Polson and Rossi (1994)'s Metropolis algorithm uses a very different approach. They approximate

the density of

h,lh\, and so use a non-Gaussian proposal based on f", Typically this procedure is considerably

slower than the use of the Gilks and Wild (1992) methods suggested above.

at University of Texas at Austin on October 5, 2011restud.oxfordjournals.orgDownloaded from

剩余32页未读，继续阅读

评论收藏

内容反馈

ZBEIYESI

粉丝: 3
资源: 8

随机波动kim（1998）论文

论文研究-随机波动率模型的参数估计及对中国股市的实证.pdf

论文研究-随机波动模型参数估计的新算法及其在上海股市的实证.pdf

随机局部波动率校准-研究论文

论文研究-随机波动和跳跃下的短期利率动态.pdf

KIM模型_能见度_能见度matlab_kim_可见光通信_

kim2007.pdf

kim055 改电压

kim2 (1)_kim_

论文研究 - 随机波动率模型下将随机相关性嵌入到FX Quanto期权的定价中

对Heston随机波动率模型的快速均值校正-研究论文

SABR随机波动率模型的人工神经网络表示-研究论文

论文研究-不规则时间序列波动率建模:高频与低频的统一.pdf

Kim一个JSON序列化和编组Python框架

kim法 目标检测

Kim Studio V1.4.exe

Matlab Deep Learning ebook Phil Kim

BOT KIM 100% bBBF_kim_MFC_源码

论文研究 - 尿NGAL和KIM-1是早产儿急性肾损伤的早期生物标志物

Hacking Vim 7.2 - by Kim Schulz,

Electric Motor Control by Sang-Hoon Kim.zip

SPAM数据挖掘Kim算法的隐写分析.pdf

Kim’s GB 迷你留言本 v0.60 Beta

tf-lstm-char-cnn:Tenorflow重写Yoon Kim的lstm-char-cnn

Tae_Kim_Grammar.apkg

最新资源

kim法目标检测