数字通信原理与技术--伪随机序列

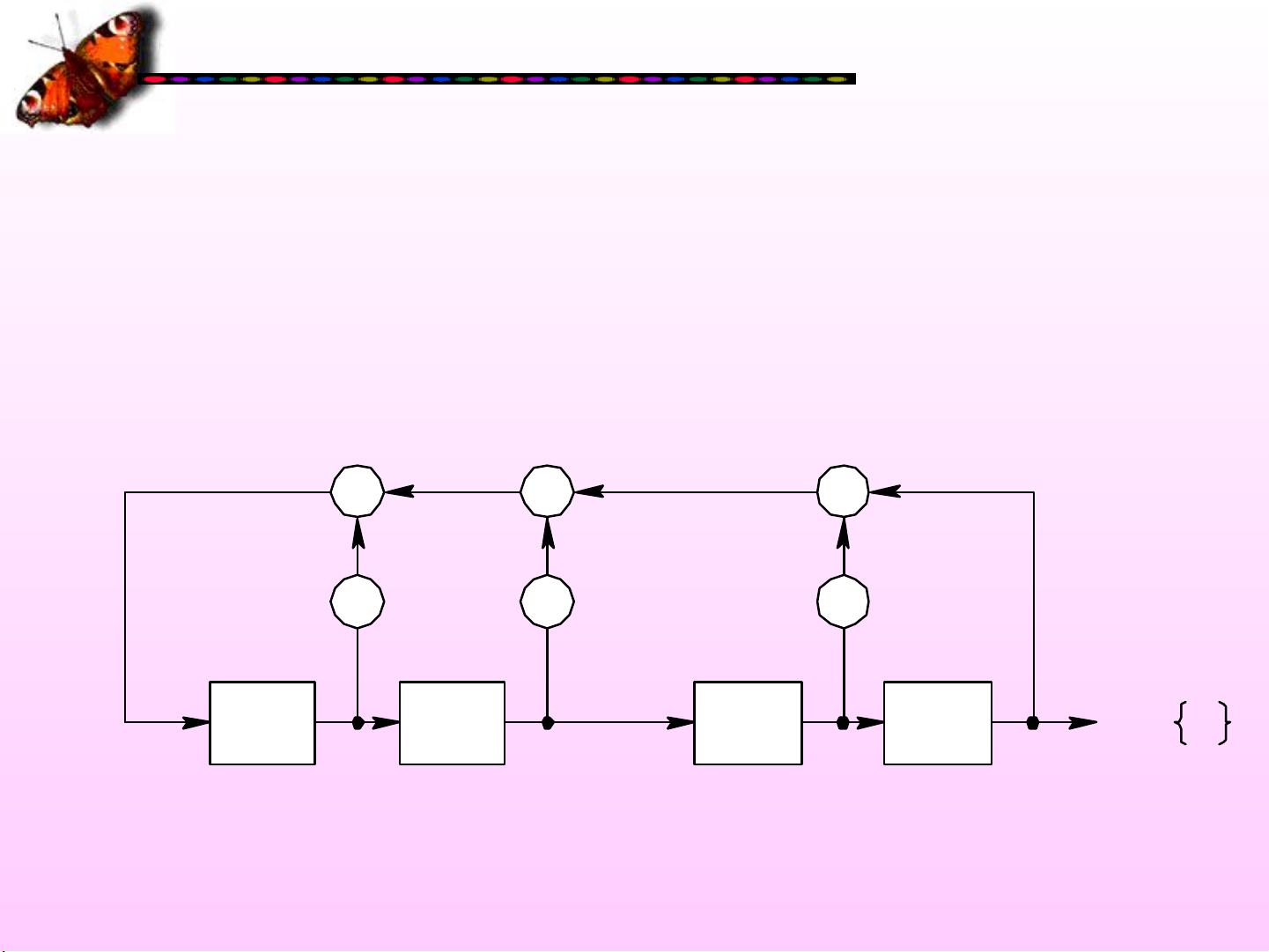
在数字通信领域，伪随机序列是一种重要的信号生成工具，广泛应用于各种通信系统中。本章节主要探讨了伪随机序列，特别是m序列的产生、性质及其应用。 **1. m序列的产生** m序列，也称为最大长度序列，是通过线性反馈移位寄存器（LFSR）生成的。LFSR是一个特殊的移位寄存器，其内部包含若干个存储单元，并且在每个移位时钟周期内，根据预设的反馈逻辑对某些位进行加法操作。图8-1展示了一个典型的LFSR结构，其中包含了反馈路径和初始状态。当LFSR处于非零初始状态时，经过一系列移位，它会生成一个具有特定周期的二进制序列。这个序列的特性由LFSR的级数、初始状态和反馈逻辑函数共同决定。如果初始状态为全零，LFSR将输出全零序列，因此需要排除这种情况。 **2. 递推关系式** 递推关系式描述了LFSR的动态行为。如第8章中所述，当LFSR经过k次移位后，第一级的输入可以通过前n个位的线性组合表示，即反馈逻辑函数。这个递推关系式有助于理解序列的生成过程。 **3. 特征多项式** 特征多项式f(x)是描述LFSR反馈连接状态的多项式。一个n次的本原多项式f(x)是满足以下条件的多项式： - f(x)是不可约的，即不能被其他非常数多项式整除。 - f(x)能整除(x^p + 1)，其中p=2^n-1，这是m序列的周期。 - f(x)不能整除任何小于p的(x^q + 1)。 **4. m序列产生器** 以n=4为例，一个4级的LFSR可以生成一个周期为p=15的m序列。选择4次本原多项式f(x)作为反馈逻辑，可以整除(x^15 + 1)。通过分解因式并找到合适的f(x)，可以构建出m序列产生器。 **5. m序列的性质** **均衡特性**：m序列在一个周期内，1的个数比0的个数多一个，这是因为周期p是奇数，1的个数是(p+1)/2，而0的个数是(p-1)/2。随着p增大，1和0出现的次数趋于平衡。 **游程特性**：游程是指序列中相同元素连续出现的子序列。m序列的游程长度分布表现出随机性，这意味着在足够大的序列中，不同长度的游程出现的概率接近于理想的随机序列。 **6. m序列的应用** m序列因其良好的统计特性，常用于通信系统的测试、同步、编码、加密以及信道仿真等方面。例如，它们可以用作伪随机噪声源，在模拟无线信道的干扰，或者在扩频通信中作为伪随机码来扩展信号的带宽。 m序列是数字通信中的关键元素，其生成原理和特性对于理解和设计高效的通信系统至关重要。通过深入理解m序列，我们可以更好地利用这些序列来优化通信性能和安全性。