
1
Implementation of Fast Fourier
Transform (FFT) on FPGA using
Verilog HDL
An Advanced-VLSI-Design-Lab (AVDL) Term-Project,
VLSI Engineering Course, Autumn 2004-05,
Deptt. Of Electronics & Electrical Communication,
Indian Institute of Technology Kharagpur
Under the guidance of
Prof. Swapna Banerjee
Deptt. Of Electronics & Electrical Communication Engg.
Indian Institute of Technology Kharagpur.
Submitted by
Abhishek Kesh (02EC1014)
Chintan S.Thakkar (02EC3010)
Rachit Gupta (02EC3012)
Siddharth S. Seth (02EC1032)
T. Anish (02EC3014)

2
ACKNOWLEDGEMENTS
It is with great reverence that we wish to express our deep gratitude towards
our VLSI Engineering Professor and Faculty Advisor, Prof. Swapna Banerjee,
Department of Electronics & Electrical Communication, Indian Institute of
Technology Kharagpur, under whose supervision we completed our work. Her
astute guidance, invaluable suggestions, enlightening comments and constructive
criticism always kept our spirits up during our work.
We would be accused of ingratitude if we failed to mention the consistent
encouragement and help extended by Mr. Kailash Chandra Ray, Graduate
Research Assistant, during our Term-Project work. The brainstorming sessions at
AVDL spent discussing various possible architectures for the FFT were very
educative for us novice VLSI students.
Our experience in working together has been wonderful. We hope that the
knowledge, practical and theoretical, that we have gained through this term project
will help us in our future endeavours in the field of VLSI.
Abhishek Kesh
Chintan S.Thakkar
Rachit Gupta
Siddharth S. Seth
T. Anish

3
1. FAST FOURIER TRANSFORMS
The number of complex multiplication and addition operations required by the simple
forms both the Discrete Fourier Transform (DFT) and Inverse Discrete Fourier Transform
(IDFT) is of order N
2
as there are N data points to calculate, each of which requires N complex
arithmetic operations.
For length n input vector x, the DFT is a length n vector X, with n elements:
In computer science jargon, we may say they have algorithmic complexity O(N
2
) and
hence is not a very efficient method. If we can't do any better than this then the DFT will not be
very useful for the majority of practical DSP applications. However, there are a number of
different 'Fast Fourier Transform' (FFT) algorithms that enable the calculation the Fourier
transform of a signal much faster than a DFT.
As the name suggests, FFTs are algorithms for quick calculation of discrete Fourier
transform of a data vector. The FFT is a DFT algorithm which reduces the number of
computations needed for N points from O(N
2
) to O(N log N) where log is the base-2 logarithm.
If the function to be transformed is not harmonically related to the sampling frequency, the
response of an FFT looks like a ‘sinc’ function (sin x) / x
The 'Radix 2' algorithms are useful if N is a regular power of 2 (N=2
p
). If we assume that
algorithmic complexity provides a direct measure of execution time and that the relevant
logarithm base is 2 then as shown in Fig. 1.1, ratio of execution times for the (DFT) vs. (Radix 2
FFT) (denoted as ‘Speed Improvement Factor’) increases tremendously with increase in N.
The term 'FFT' is actually slightly ambiguous, because there are several commonly used
'FFT' algorithms. There are two different Radix 2 algorithms, the so-called 'Decimation in Time'
(DIT) and 'Decimation in Frequency' (DIF) algorithms. Both of these rely on the recursive
decomposition of an N point transform into 2 (N/2) point transforms. This decomposition process
can be applied to any composite (non prime) N. The method is particularly simple if N is
divisible by 2 and if N is a regular power of 2, the decomposition can be applied repeatedly until
the trivial '1 point' transform is reached.
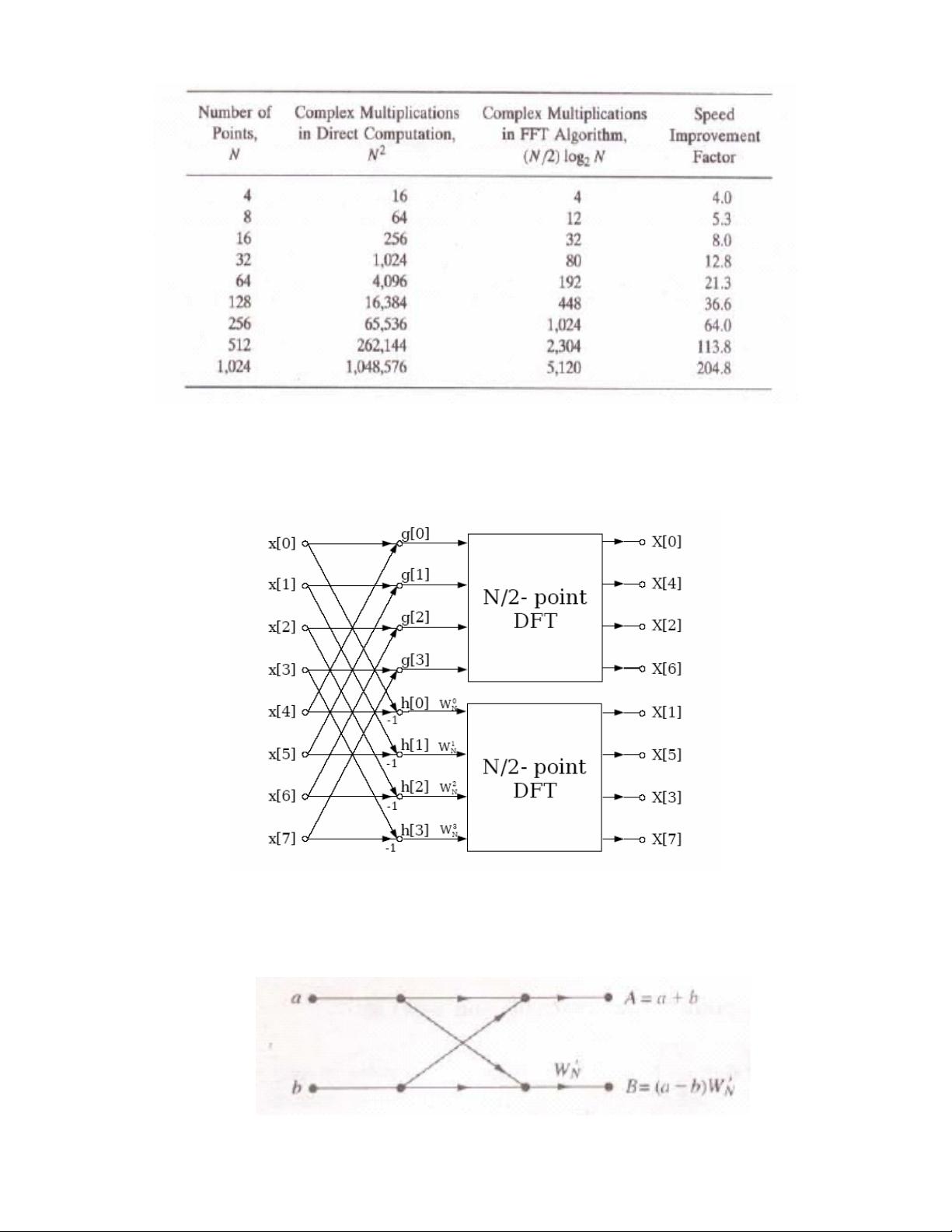
4
Fig. 1.1: Comparison of Execution Times, DFT & Radix – 2 FFT
The radix-2 decimation-in-frequency FFT is an important algorithm obtained by the divide-
and-conquer approach. The Fig. 1.2 below shows the first stage of the 8-point DIF algorithm.
Fig. 1.2: First Stage of 8 point Decimation in Frequency Algorithm.
The decimation, however, causes shuffling in data. The entire process involves v = log
2
N
stages of decimation, where each stage involves N/2 butterflies of the type shown in the Fig. 1.3.
Fig. 1.3: Butterfly Scheme.

5
Here W
N
= e
–j 2Π/ N,
is the Twiddle factor.
Consequently, the computation of N-point DFT via this algorithm requires (N/2) log
2
N
complex multiplications. For illustrative purposes, the eight-point decimation-in frequency
algorithm is shown in the Figure below. We observe, as previously stated, that the output
sequence occurs in bit-reversed order with respect to the input. Furthermore, if we abandon the
requirement that the computations occur in place, it is also possible to have both the input and
output in normal order.
Fig. 1.4: 8 point Decimation in Frequency Algorithm
















