匈牙利算法及二分图知识专题讲解
匈牙利算法,也称为Edmonds算法,是一种用于解决二分图最大匹配问题的有效方法。在二分图中,顶点被分为两部分X和Y,边连接这两部分的顶点。匈牙利算法的主要目标是在这样的图中找到最大的匹配,即尽可能多地找到X和Y之间的配对,使得每条边都只属于一个配对,且没有两个配对共享同一边。 算法的核心步骤如下: 1. 初始化:用(*)标记所有未匹配的X顶点。 2. 遍历过程:交替执行步骤2和3。对于步骤2,选择一个刚标记过的X顶点xi,如果它与一个尚未被标记的y形成非匹配边,那么用(xi)标记y。对于步骤3,选择一个刚用(xi)标记过的Y顶点yi,如果它与一个尚未被标记的x形成匹配边,那么用(yi)标记x。 3. 回溯与交替链:当找到一个Y顶点y,它不是M顶点时,回溯找到一条交替链。交替链由匹配边和非匹配边交替组成,可以用来增加匹配的数量。 4. 修改匹配:将交替链中的非匹配边改为匹配边,匹配边改为非匹配边,形成新的匹配M,然后回到步骤1,清除所有标记。 5. 终止条件:如果无法找到满足条件的顶点进行标记,且不存在交替链,算法结束。此时,M即为当前的最大匹配。 通过这个算法,每次能找到一条从未匹配顶点到未匹配顶点的交替链,修改匹配后,匹配数会增加。重复这个过程,直到无法找到这样的链为止。 在给定的代码示例中,`check`函数用于检查男孩和女孩是否满足恋爱条件,构建了一个二分图,其中男孩和女孩分别代表图的两部分,满足条件的男女之间建立边。`Path`函数则是实现算法中寻找交替链的步骤,通过回溯找到从未匹配顶点到另一个未匹配顶点的路径。最终,`n-max_number_of_couples`给出了满足条件的最大人数,即不会恋爱的人数。 通过理解和应用匈牙利算法,我们可以解决许多实际问题,如资源分配、任务调度和二分图的最大匹配问题。在给定的练习题"Guardian of Decency"中,就是要找出在满足特定规则的情况下,最多可以有多少人不组成情侣,从而实现资源的最大化利用。

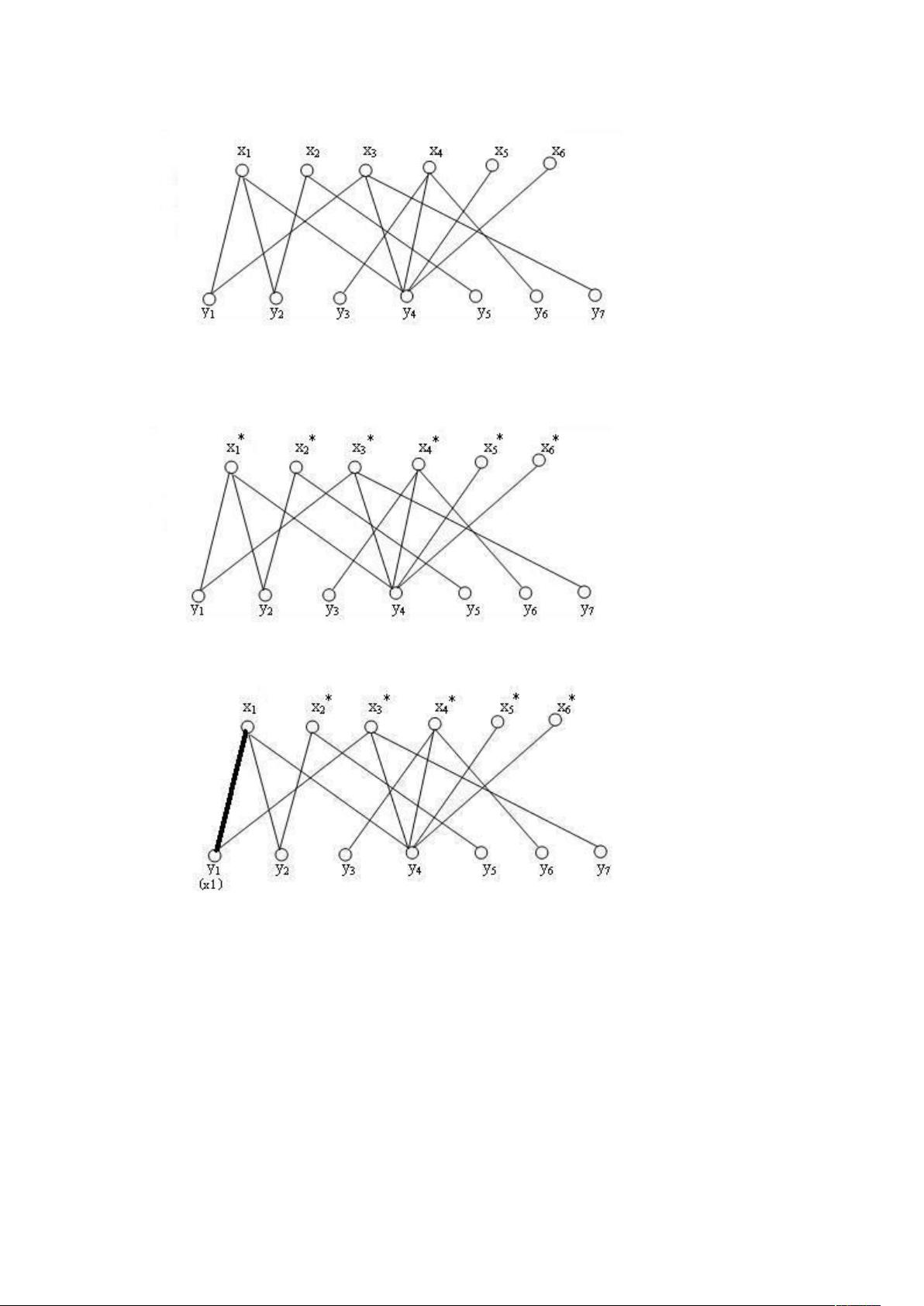
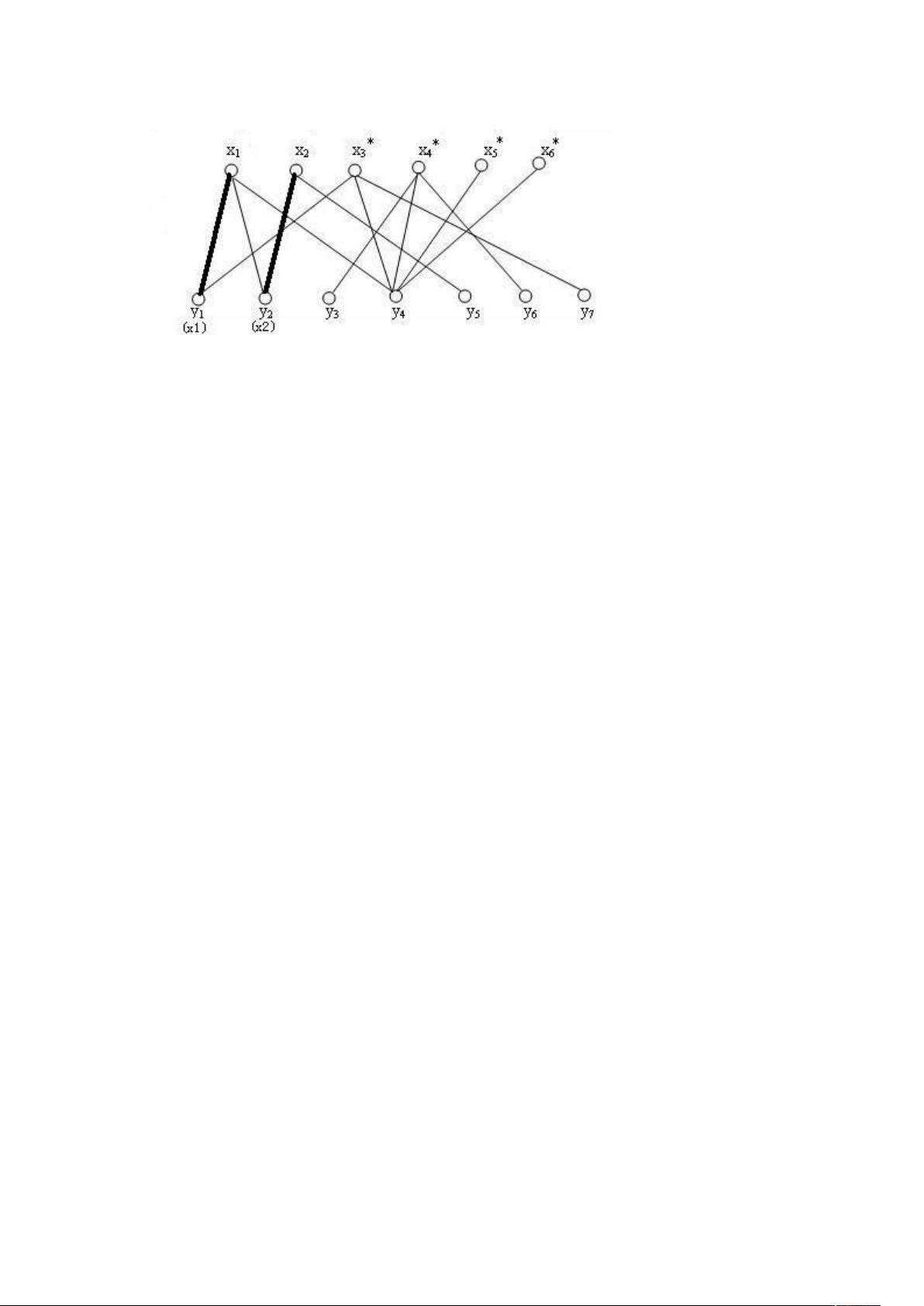
剩余13页未读,继续阅读

 vcdaren2015-02-04匈牙利算法比较复杂,需要一定的耐心才能看得懂
vcdaren2015-02-04匈牙利算法比较复杂,需要一定的耐心才能看得懂
- 粉丝: 17
- 资源: 6
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功