函数同构问题-解析版.pdf

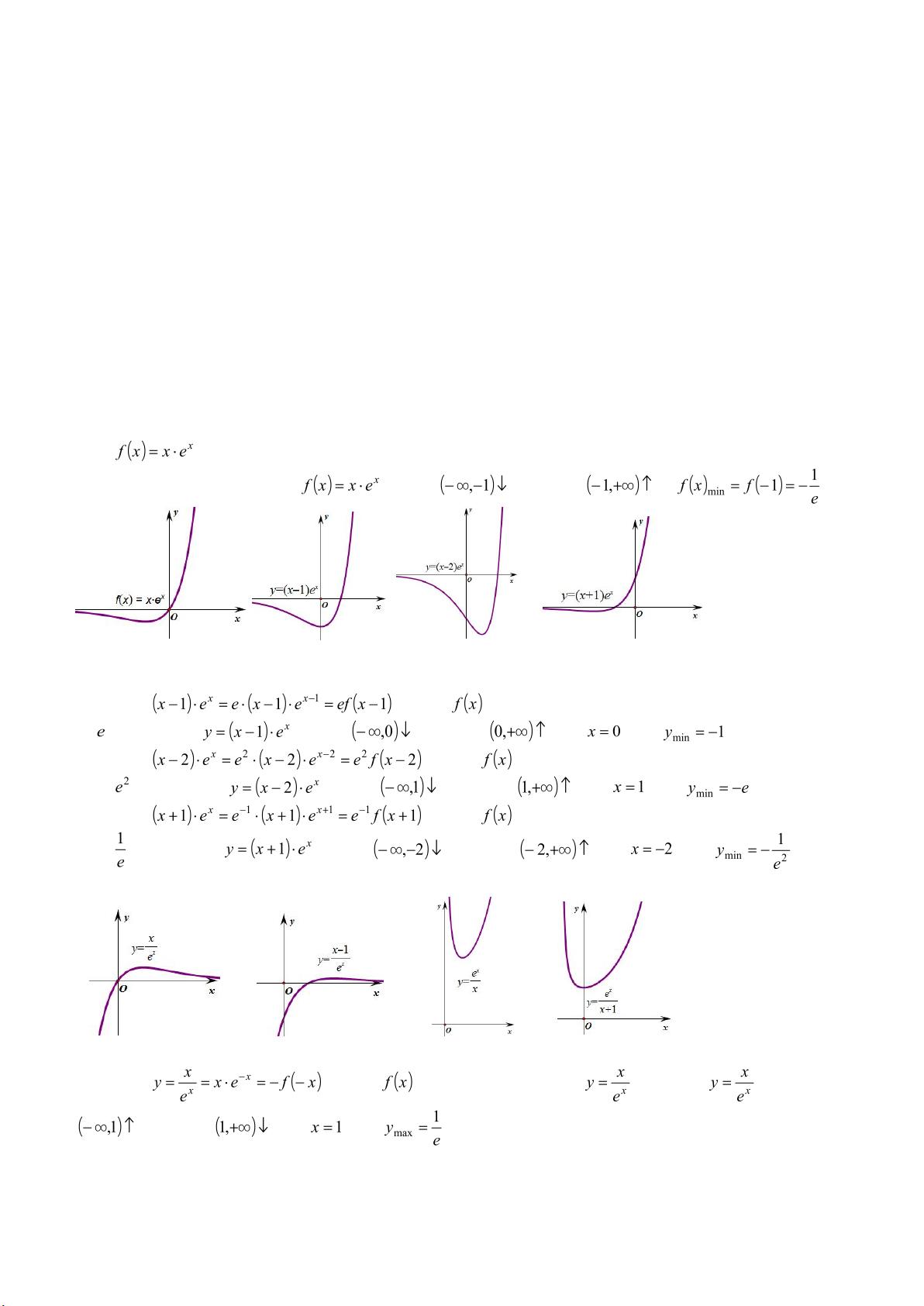
《函数同构问题》主要探讨了函数在不同变换下的同构关系，以及如何利用这些关系解决各类不等式和方程的问题。以下是该主题的主要知识点： 1. **顺反同构**： - **顺同构**：通过平移和拉伸函数图形，保持其基本性质不变。例如，函数`f(x)`向右平移`a`个单位，纵坐标扩大`k`倍，形成新函数`f(x-a)`，在适当区间内，它们的性质如单调性、极值等保持一致。 - **反同构**：通过乘除操作改变函数的凹凸性。例如，将函数关于原点对称，或者进行比例缩放，可能导致函数的凹凸性反转。 2. **同位同构**： - **加减同构**：通过加减运算组合，构造出新的同构函数。这常用于简化问题，例如，通过配凑实现同构。 - **局部同构**：针对函数的特定部分进行构造，比如跨阶和指数幂与对数真数差1的情况，可快速找到同构函数。 - **差一同构**：处理跨越不同阶数或指数与对数形式的函数，通过巧妙的转化实现同构。 3. **应用实例**： - 不等式恒成立问题：通常涉及求参数的取值范围，通过同构函数的关系转换，找到等价条件。 - 方程的根的问题：通过分析函数的性质，确定实数根的存在性和唯一性。 - 函数单调性分析：通过求导判断函数的单调区间，进而解决最值问题。 4. **证明技巧**： - 构造辅助函数：为了证明某个结论，常需要构造一个新的函数，利用不等式的性质来证明目标函数的特性。 - 利用导数研究函数的极值和单调性：通过求导数，找到函数的临界点和单调区间，帮助理解函数的行为。 5. **解题策略**： - 图像法：通过画图直观理解函数的变化，找出同构关系。 - 最值法：寻找函数的最大值或最小值，用以建立不等式或确定参数范围。 - 对比法：比较不同形式的函数，找出它们在同构关系下的相似性。 6. **具体问题举例**： - 通过平移和拉伸，如题目中的图2、图3、图4所示，可以确定新的函数表达式及其性质。 - 乘除操作导致的凹凸反转，如图5至图8，通过对称和比例变换，得出新的同构函数。 这些知识点在解决复杂的数学问题时起着关键作用，尤其是当涉及到函数的性质分析和不等式的恒成立问题时，同构思想能提供有效的解决方案。通过理解和掌握这些概念，不仅可以提高解题效率，还能加深对函数本质的理解。