高中数学 322对数及其运算学案(2)新人教B版必修1 学案.doc

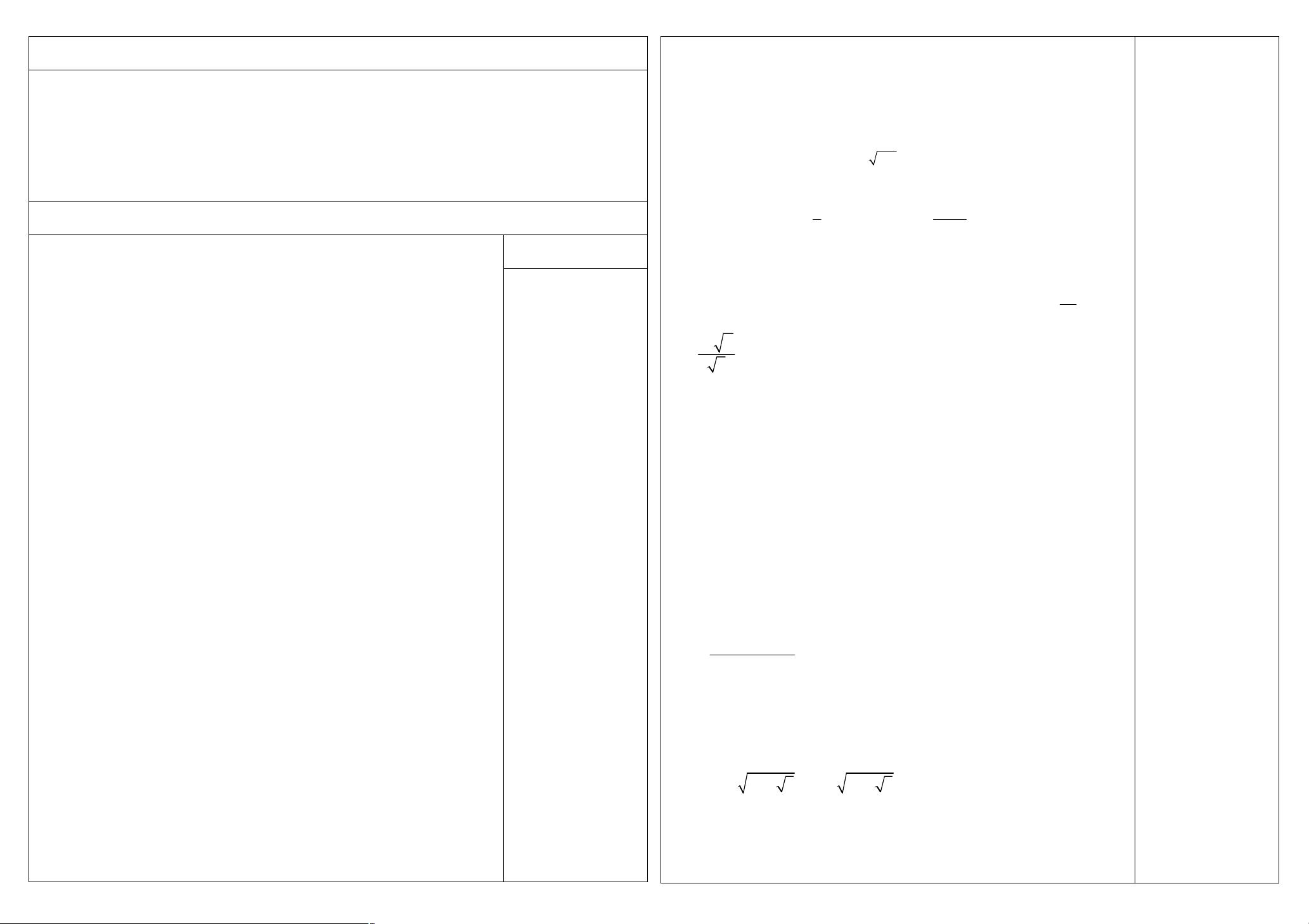
【对数及其运算】 在高中数学的3.2.2章节中，我们主要学习的是对数及其运算法则。对数是一种将指数运算转化为乘法运算的工具，它在数学和实际问题中都有广泛的应用。新人教B版必修1的这部分内容着重于理解和运用对数的运算性质。 我们要掌握三个基本的对数运算性质： 1. 积的对数等于对数的和：\( \log_a(MN) = \log_a M + \log_a N \) 2. 商的对数等于对数的差：\( \log_a\left(\frac{M}{N}\right) = \log_a M - \log_a N \) 3. 幂的对数等于指数乘以底数的对数：\( \log_a(M^n) = n \cdot \log_a M \) 在应用这些性质时，需要注意对数的底数 \( a \) 必须大于0且不等于1，同时，对数的真数 \( M \) 和 \( N \) 必须大于0。例如，\( \log_{10}(5^3) = 3 \cdot \log_{10}5 \)。此外，还需要留意某些错误的记忆，比如 \( \log_M N \neq \log_N M \)，因为对数运算并不遵守交换律。 在自学检测部分，我们需要解决一些基于对数运算的问题，例如，如果 \( \log_{10}a = m \) 和 \( \log_{10}b = n \)，那么可以表示： 1. \( 5\log_{10}25 = 5m \) 2. \( 0.4\log_{10}1 = 0 \) 3. \( 8\log_{10}2^4 \cdot 3^{-1} = 8 \cdot 4m \cdot (-\frac{1}{3}) \) 4. \( \log_{10}9 - \log_{10}100 = m - 2 \) 在合作探究环节，我们通过例题进一步加深对对数运算的理解，例如： 1. \( \log_{a}xyz = \log_{a}x + \log_{a}y + \log_{a}z \) 2. \( 2^3\log_{a}xyz = 3(\log_{a}x + \log_{a}y + \log_{a}z) \) 3. \( \log_{2}4^3 - 3\log_{2}4 = 3\cdot 2 - 3 \cdot 1 \) 4. \( \log_{8}4^2 - 3\log_{8}4 = 2\cdot \frac{2}{3} - 3\cdot \frac{1}{3} \) 变式练习和当堂检测的题目旨在巩固对数的运算法则，并通过实际计算来提高熟练度。例如，如果 \( 5^a = 3^b = 2^c \)，那么 \( a, b, c \) 之间存在怎样的关系？或者，如果 \( \log_{a}x + \log_{a}y = c \)，如何求解 \( x \)？ 课堂小结中，我们需要回顾对数的定义、性质以及它们在解决复杂问题中的应用。而分层训练部分则进一步挑战我们的对数运算技能，包括对等式的条件分析和对对数性质的综合运用。 本节课程重点在于理解和熟练运用对数的运算性质，包括加减乘法的转换，以及解决涉及对数的复杂表达式。通过大量的练习和实例，我们可以提升对数运算的能力，为后续的数学学习打下坚实的基础。