
四川大学电气工程学院
信号与系统实验报告
(本科)
学 号 2020141440385
姓 名 许昊天
专 业 电气工程及其自动化
任课老师 刘亚梅 钟俊
日 期 2022.6.7
实验题目 LTI 系统传输函数零极点图与单位阶跃响应

实验 4
一、 实验目的
1.
掌握系统函数、零点和几点的求解及含义;
2.
掌握系统传递函数零极点与系统稳定性、单位冲激响应和单位阶跃响应
终值的联系
二、 实验内容
给定一个以微分方程描述的
LTI
系统
1
、理论分析
(
a
) 系统的传递函数,零点和极点,判断系统的稳定性;
(
b
) 求系统的单位冲击响应和单位阶跃响应;
(
c
) 求以上响应的初值和终值。
2
、仿真分析
(
a
) 绘制系统的零极点图
(
b
) 画出系统单位冲激响应和单位阶跃响应的波形;
(
c
) 分析。
三、 参数 a=-1 时
以微分方程描述的
LTI
系统,其微分方程为
1. 理论分析
对于给定的微分方程的两端进行拉普拉斯变换,得到系统的传递函数
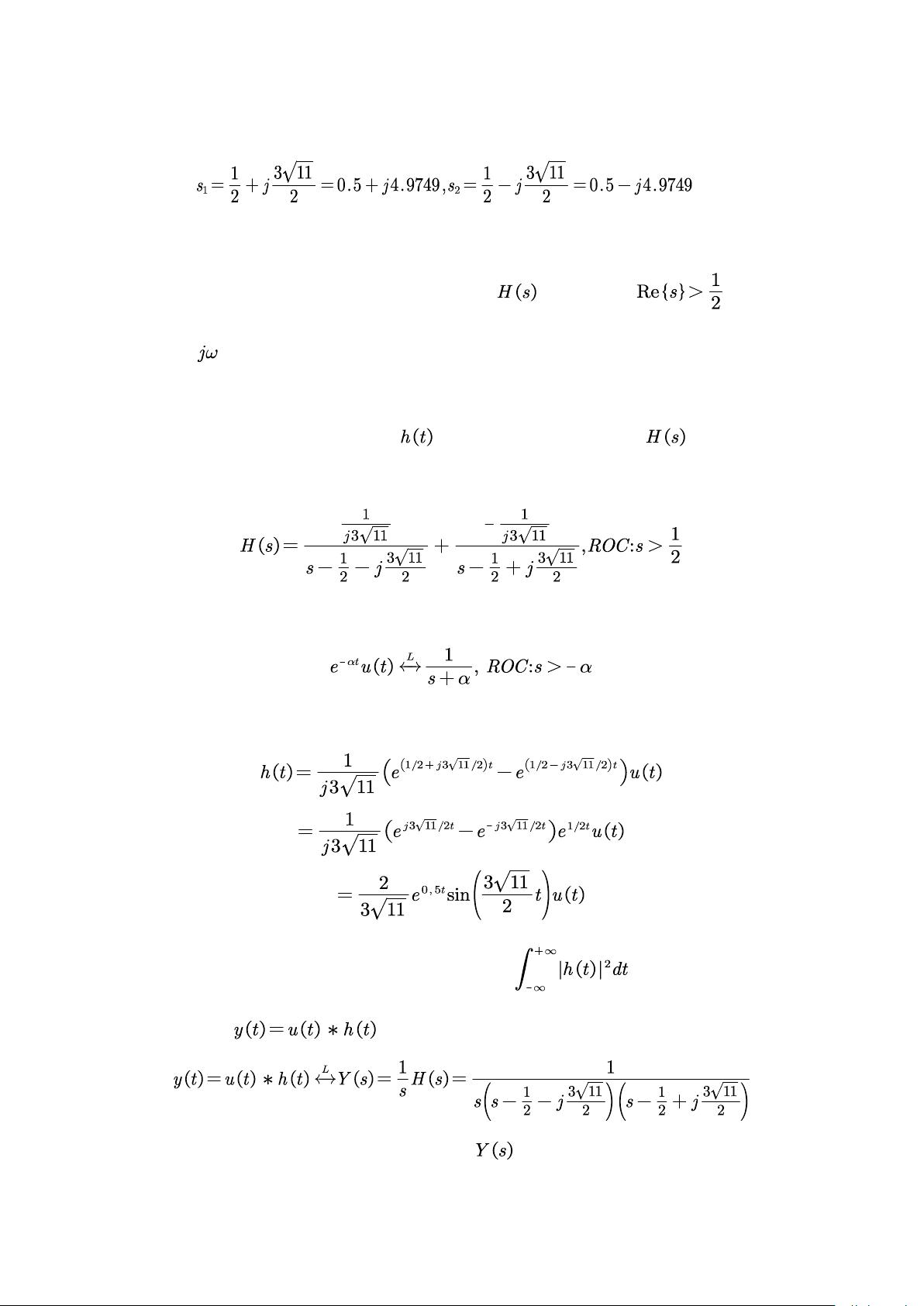
求解传递函数的零极点
极点:
无零点
由于系统是因果系统,故系统传递函数 的收敛域为 。由于
不包含 轴,因此该系统的传递函数不存在傅里叶变换,即该系统是一个不稳
定系统。
为求解系统的单位冲激响应 ,只需要对系统传递函数 进行拉普拉
斯反变换即可。对系统传递函数进行有理分式分解:
由拉普拉斯常用变换对
对系统函数进行逆变换得到
显然单位冲激响应不满足绝对可和的性质 为求解出系统的阶
跃响应,即 ,根据拉普拉斯的卷积性质
同理求解冲激响应的步骤将复频域表达式 进行有理分式分解得到

逆变换得到
根据拉普拉斯的初值定理
计算出单位冲激响应的初值和单位阶跃响应的初值
该结果与直接带入单位冲激响应和单位阶跃响应的时域表达式所得结果一致。
根据拉普拉斯的终值定理
但由于 在 平面的右半边也存在极点,不满足终值定理的条件。故采
用直接带入时域表达式求解其终值。由于时域表达式中的指数为正,故其终值
为无穷大。
2. 仿真分析
绘制系统的零极点图
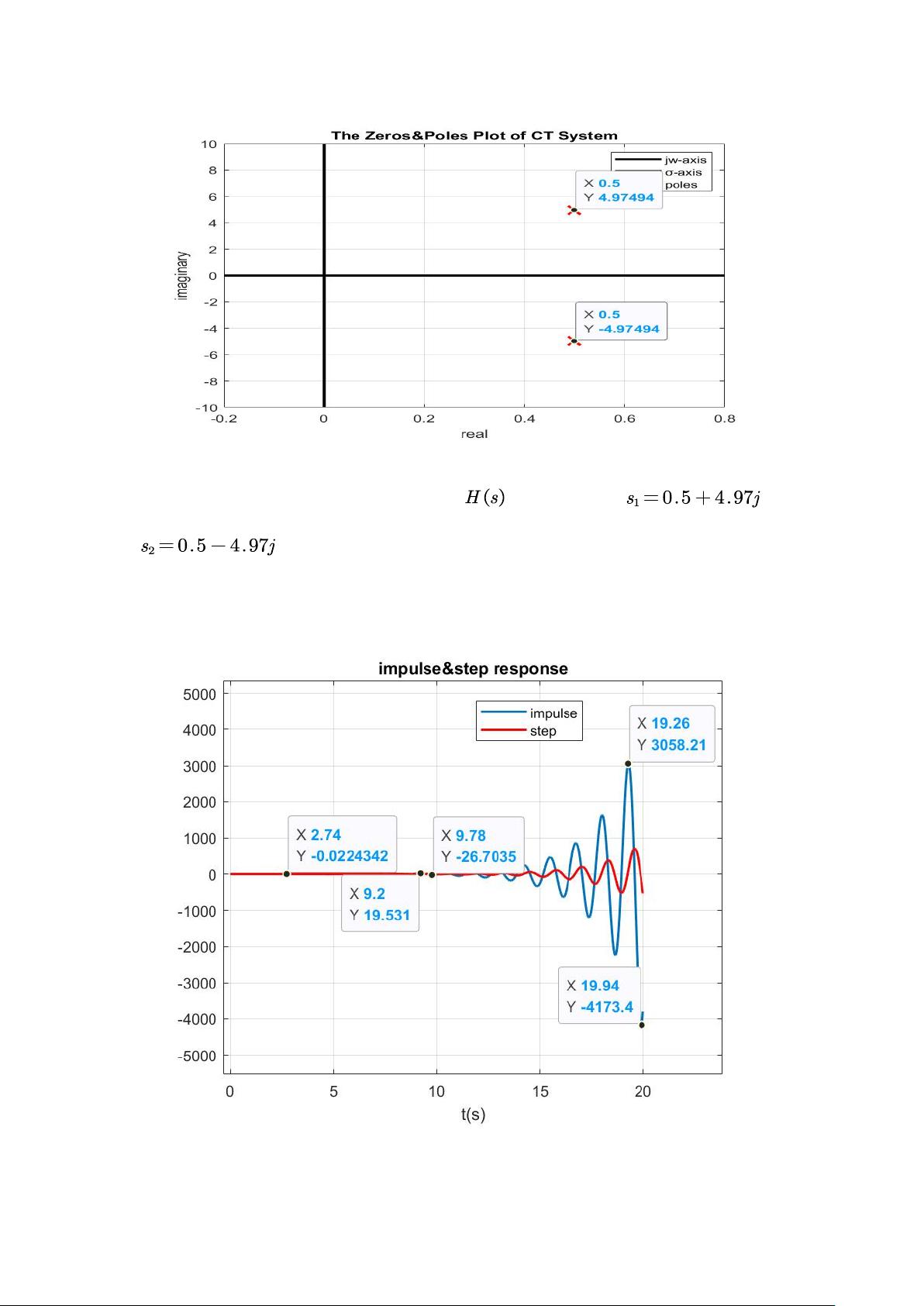
图
1 a=-1
时系统的零极点图
由零极点图可知该系统的特征函数 的极点分布在 和
,无零点。分别呈共轭对称分布,故系统的单位冲激响应是一
个实函数。
画出系统单位冲激响应和单位节约响应的波形
图
2 a=-1
时系统的单位冲激响应和单位阶跃响应
由零极点图可知,该 LTI 是一个因果不稳定系统,为更好的观察系统的不
















