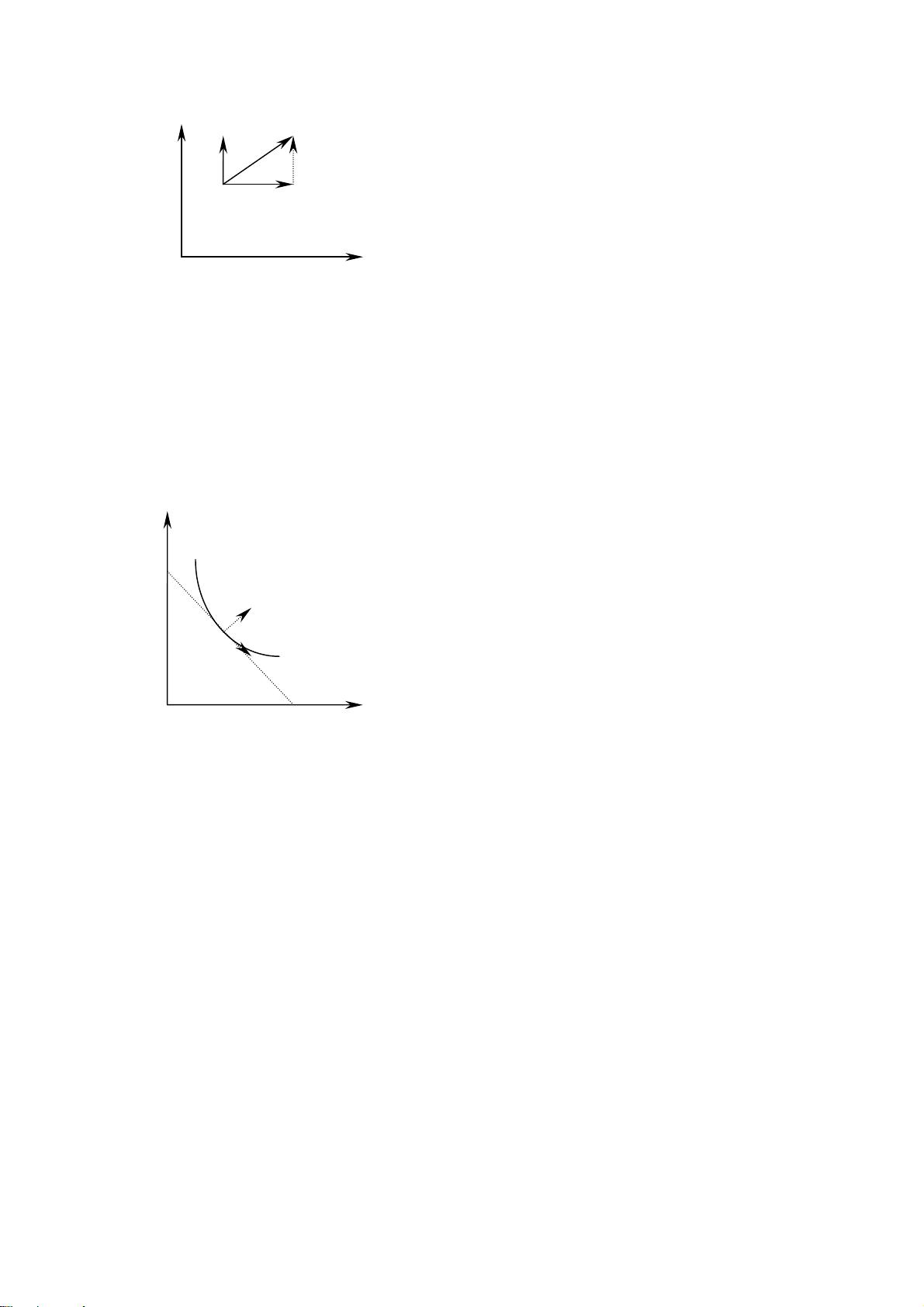
最优化与KKT条件

### 最优化与KKT条件 #### 一、最优化理论概览 最优化问题是数学、经济学、工程学等多个学科中的核心问题之一。它涉及到如何在给定的条件下找到最佳解决方案，即最大化或最小化某个目标函数的过程。在《最优化与KKT条件》这份文档中，作者冯曲教授详细介绍了最优化的基本理论以及KKT（Karush-Kuhn-Tucker）条件，这些内容对于理解和解决最优化问题至关重要。 #### 二、最优规划问题概述 最优规划问题通常涉及寻找使目标函数达到最大或最小的变量值，同时还需要满足一定的约束条件。这类问题可以形式化地表示为： \[ \max_{x} f(x) \quad \text{s.t.} \quad g(x) = c \] 这里，\(f(x)\) 是目标函数，\(x\) 是决策变量，\(g(x)\) 是约束函数，而 \(c\) 是常数值。目标是找到满足约束条件的 \(x\) 值，使得目标函数 \(f(x)\) 的值最大化。 #### 三、梯度向量与最优化 梯度向量是理解最优化问题的关键工具之一。梯度向量给出了函数增长最快的方向，并且其模长表示了该方向上的增长速度。 ##### 1. 无约束极值问题 在一维情况下，梯度可以简化为导数。考虑函数 \(f(x)\)，其在某点 \(x\) 处的微小变化可表示为： \[ df = f'(x) dx \] 这表明，函数的变化量 \(df\) 可以通过函数的导数 \(f'(x)\) 与自变量的微小变化 \(dx\) 相乘得到。 ##### 2. 约束极值问题 在多维情况下，梯度向量 \(\nabla f\) 给出了函数 \(f\) 在某点的增长方向。对于受约束的最优化问题，需要考虑约束条件对梯度的影响。 #### 四、拉格朗日乘数法与等式约束极值问题 对于带有等式约束的最优化问题，可以使用拉格朗日乘数法来求解。这种方法通过引入拉格朗日函数： \[ L(x, \lambda) = f(x) - \lambda(g(x) - c) \] 其中，\(\lambda\) 称为拉格朗日乘数，是未知参数。通过求解拉格朗日函数关于 \(x\) 和 \(\lambda\) 的偏导数等于零的条件，可以获得原问题的解。 #### 五、KKT条件 当处理含有不等式约束的最优化问题时，KKT条件提供了一套必要的条件，用于判断一个点是否可能是最优解。这些条件包括： 1. **原点条件**：约束必须满足。 2. **拉格朗日条件**：目标函数的梯度必须等于拉格朗日乘数与每个约束的梯度的线性组合。 3. **互补松弛条件**：若某个不等式约束被满足，则对应的拉格朗日乘数为零；反之，若乘数非零，则约束恰好取等号。 4. **线性独立约束资格条件**（LICQ）：约束函数的雅可比矩阵的列是线性独立的。 5. **线性约束资格条件**（LCQ）：所有不等式约束的雅可比矩阵的列与等式约束的雅可比矩阵的列共同形成线性独立集。 6. **Mangasarian-Fromovitz约束资格条件**（MFCQ）：存在一个非零向量，使得该向量与所有不等式约束的雅可比矩阵的列垂直，且与等式约束的雅可比矩阵的列正交。 #### 六、二阶条件 二阶条件是确定极值点性质的重要条件。对于无约束极值问题，可以通过二阶泰勒展开来判断极值点类型。如果Hessian矩阵是正定的，则表明该点是局部最小值点；如果是负定的，则是局部最大值点；如果既不是正定也不是负定，则该点可能既不是最小也不是最大值点。 #### 七、凹规划 凹规划是一类特殊的最优化问题，其目标函数是凹函数，约束集是凸集。对于凹规划问题，任何局部最小值都是全局最小值，因此可以通过求解局部极小值来获得全局最优解。 #### 八、最优化问题的解 解决最优化问题时，首先需要考虑解的存在性和唯一性。根据Weierstrass定理，如果目标函数在紧集上连续，则存在至少一个极值点。此外，还讨论了解的分离性，这对于多目标优化问题尤为重要。 #### 九、比较静态分析与包络定理 比较静态分析探讨了参数变化对最优解的影响。包络定理则关注于最优解随着某些参数的变化而产生的效应。这些工具对于理解最优解随外部条件变化的行为非常重要。 《最优化与KKT条件》提供了深入浅出的最优化理论介绍，不仅涵盖了基本的概念和方法，而且还详细解释了如何应用这些理论来解决实际问题。这对于从事数学、经济学以及工程领域的研究人员和实践者来说，是一份宝贵的参考资料。