理解KKT条件1

from https://www.zhihu.com/question/58584814

理解KKT条件

本笔记是对（凸）优化理论中拉格朗日乘子法和KKT条件的理解和总结，大量参考了如下资料：

Convex Optimization, Stephen Boyd and Lieven Vandenberghe, Cambridge University

拉格朗日乘子法和KKT条件

如何通俗地讲解对偶问题？尤其是拉格朗日对偶lagrangian duality？

一句话总结：KKT条件就是无约束优化问题中最优值点的必要条件（导数为0）在包含等式约束和不等式约束的优

化问题中的推广，它是基于拉格朗日乘子法得来的。

我们先来考虑一种简单的情况，有如下优化问题

该问题只含有一个等式约束，其目标函数和约束函数可以用二维平面来表示：

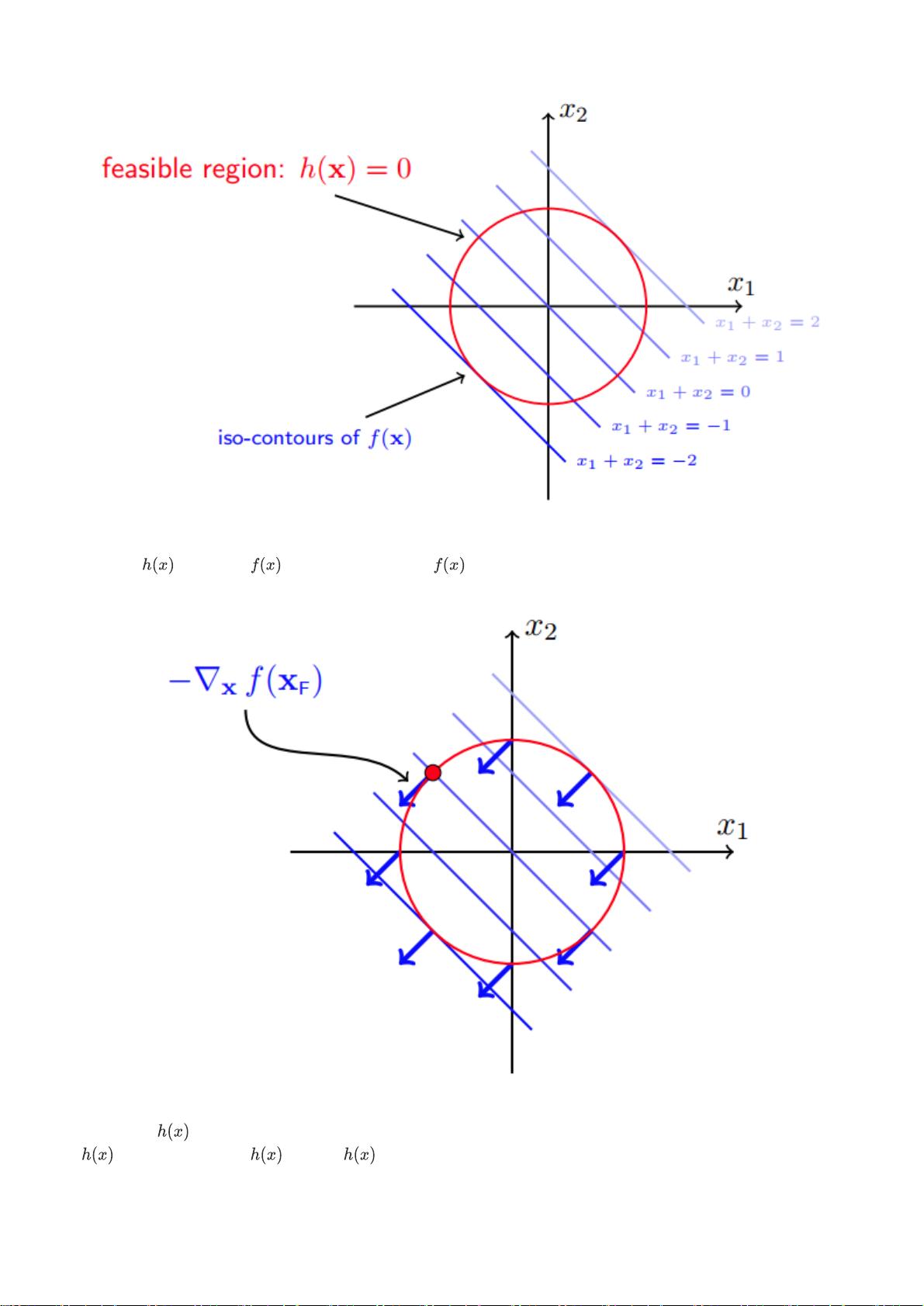
from https://www.cnblogs.com/liaohuiqiang/p/7805954.html

from https://www.cnblogs.com/liaohuiqiang/p/7805954.html

不考虑圆 的限制时， 要得到极小值，需要往 的负梯度（下降最快的方向）方向走，如下图蓝色箭

头。

如果考虑圆 的限制，要得到极小值，需要沿着圆的切线方向走，如下图红色粗箭头。注意这里的方向不是

的梯度，而是正交于 的梯度， 梯度如下图的红色细箭头。