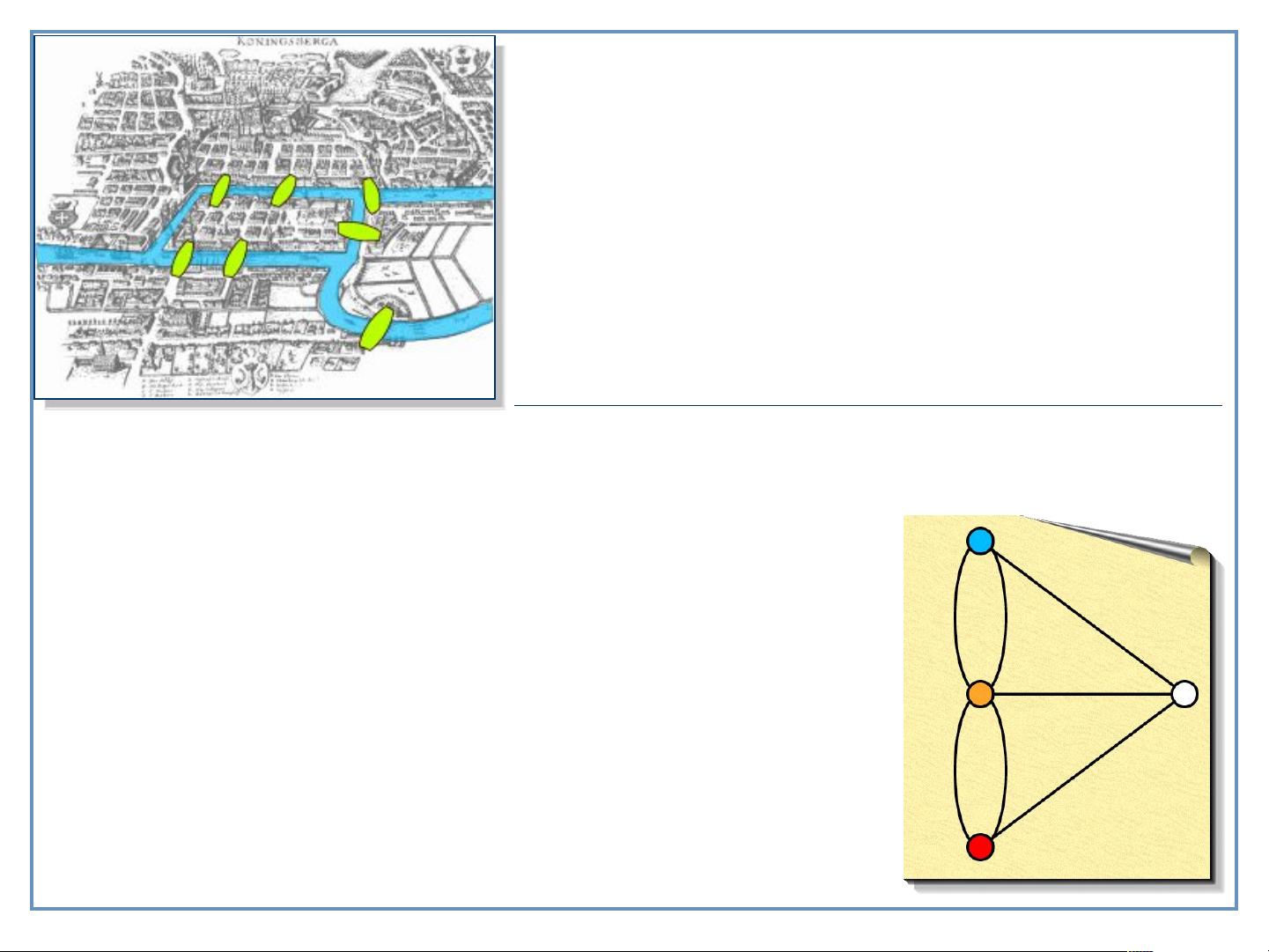
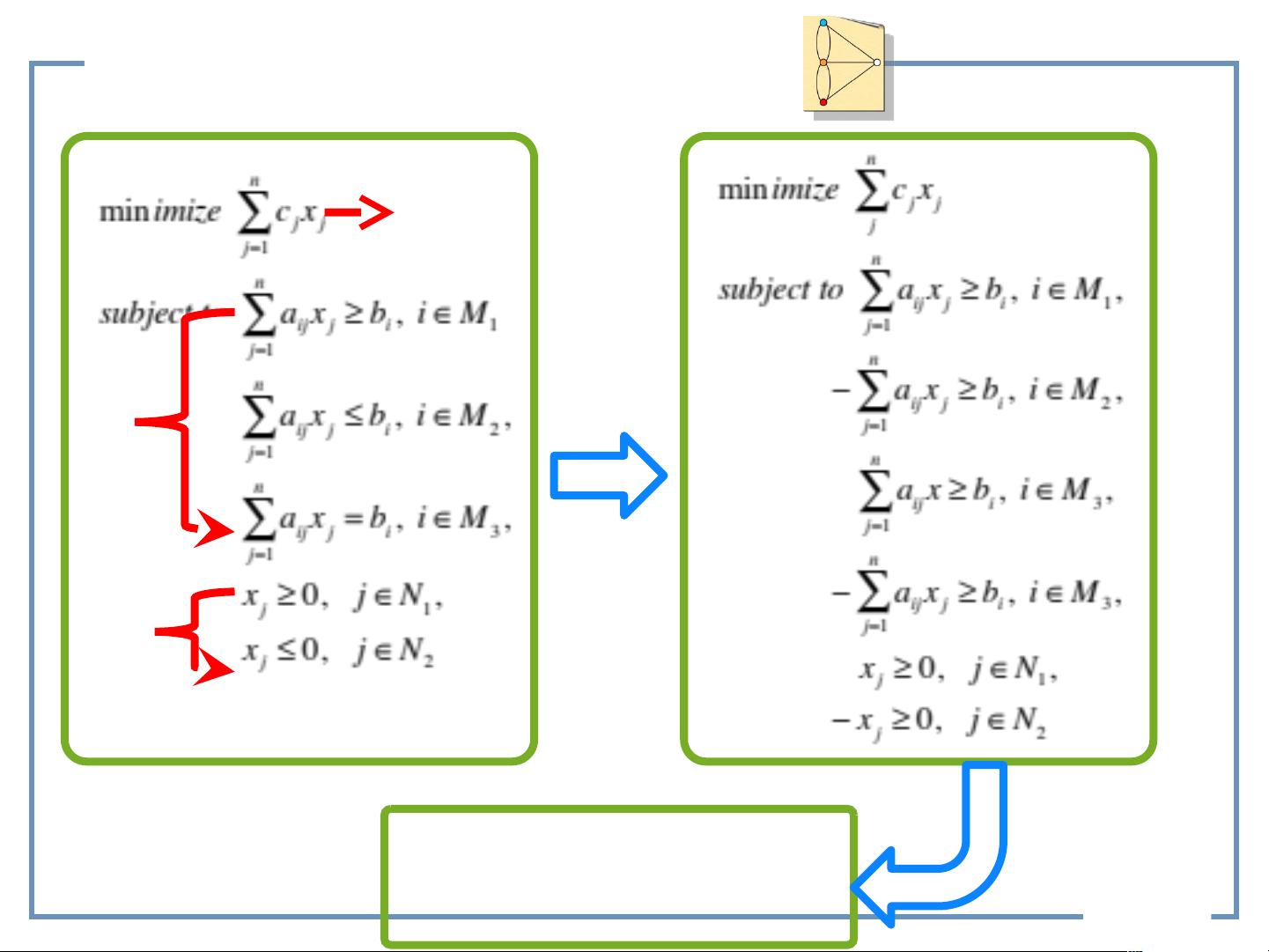
【通信网理论基础：线性规划建模】
线性规划是一种优化方法，广泛应用于解决通信网络中的各种资源分配和调度问题。在这个主题中，我们主要关注如何利用线性规划来解决网络优化问题，如最大流问题和最小费用流问题。
**线性规划模型的基本概念**
线性规划模型由以下三部分组成：
1. **决策变量**（Decision Variables）：这些是模型中可以调整的未知数，通常代表网络中的流量、资源分配量等。例如，在生产问题中，每种产品的生产量 `xj` 就是决策变量。
2. **优化目标**（Objective Function）：模型试图最大化或最小化的量。在上述生产问题中，目标是最总利润最大化，可以表示为 `minimize` 或 `maximize` 各产品利润之和。
3. **约束**（Constraints）：限制决策变量的条件。在生产问题中，这些约束可能包括原料的可用量、产品的生产能力和市场需求。在网络优化问题中，常见的约束有流量守恒（即入流量等于出流量）和容量约束（边的最大流量不能超过其容量）。
**最大流问题建模**
最大流问题是寻找网络中从源节点 `s` 到汇点 `t` 的最大流量，同时满足流守恒和容量约束。决策变量是每条边 `(i, j)` 上的流量 `xij`，目标是使总流量最大化。这个问题可以用一组线性等式和不等式来表示，如流量守恒约束 `xij + xji = 0` 对于非源汇节点，以及容量约束 `xij ≤ capacity(i, j)`。
**最小费用流问题建模**
最小费用流问题是在保证一定流量 `v` 从 `s` 流到 `t` 的同时，寻求最小化流动的总费用。每个边 `(i, j)` 有单位流的代价 `cij`，目标函数变为最小化总费用。此问题同样可以通过线性规划解决，但目标函数变为 `minimize` 流的总费用，而不仅仅是最大化流量。
**Node-Link 模型**
Node-Link 模型是一种用于网络优化的建模方式，其中约束定义在节点上（流量守恒），而变量定义在边（流变量）上。关联矩阵 `N` 描述了节点与边的关系，帮助表述流量守恒约束。
**总结**
通信网络优化中的线性规划建模涉及到选择合适的决策变量，设置精确的优化目标，以及制定合理的约束条件。通过这种方式，我们可以解决实际问题，如生产计划、护士排班、网络资源调度等，以实现最大效率或最小成本。线性规划模型不仅可以用于最大流和最小费用流问题，还可以扩展到多商品流问题和其他复杂网络优化问题。理解和应用这些模型对于优化通信网络的性能至关重要。
