工学机械优化设计PPT学习教案.pptx

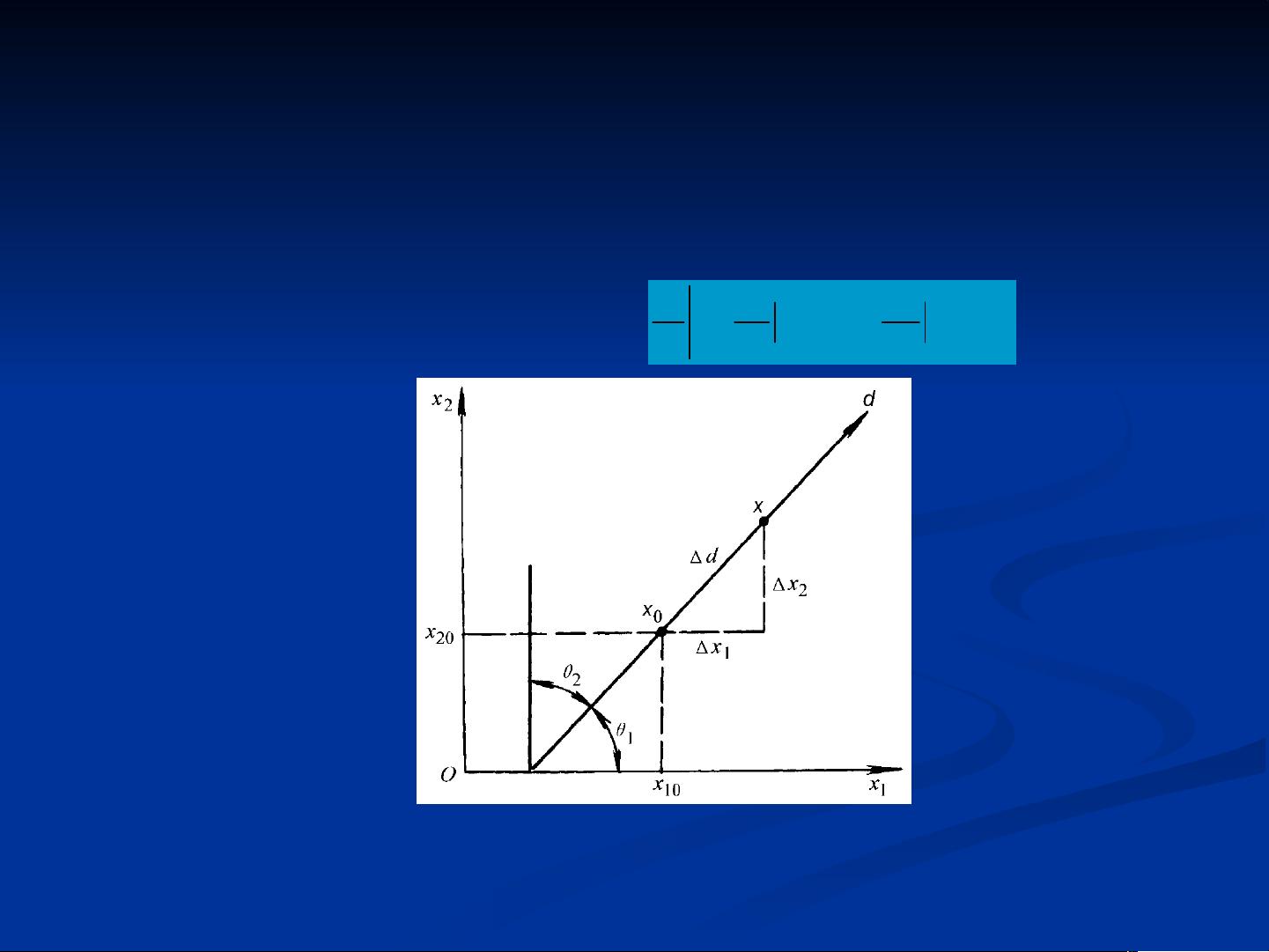
【工学机械优化设计】是工程领域中一个重要的主题，主要关注如何通过数学方法来优化机械设备的设计，以达到性能最佳、成本最低或效率最高的目标。本PPT学习教案主要介绍了优化设计的数学基础，包括方向导数和梯度的概念。 **一、方向导数** 方向导数是多变量函数在某一点沿着特定方向的变化率。对于函数f(x1, x2)，在点(x10, x20)处的方向导数定义为沿着方向向量d的变化率。若d是一个单位向量，方向导数表示为： \[ \lim_{{\Delta x_1 \to 0, \Delta x_2 \to 0}} \frac{f(x_1 + \Delta x_1, x_2 + \Delta x_2) - f(x_1, x_2)}{\Delta x_1 + \Delta x_2} \] **二、二元函数的梯度** 梯度是函数在某点的偏导数组成的向量，它表示了函数在各个方向上的变化率。梯度的方向是函数值增加最快的方向，其模长是最大变化率。在二维空间中，梯度表示为： \[ \nabla f = (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}) \] **三、多元函数的梯度和方向导数** 这个概念可以扩展到更高维度的函数。对于n元函数f(x1, x2, ..., xn)，梯度定义为： \[ \nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n}) \] 方向导数是梯度与任意向量d的点积，表示函数在d方向上的变化率。 **四、多元函数的泰勒展开** 泰勒展开是用多项式近似函数的一种方法。一元函数的泰勒展开以中心点展开，而二元函数的泰勒展开式则考虑了所有偏导数，如： \[ f(x_1, x_2) \approx f(x_{10}, x_{20}) + \frac{\partial f}{\partial x_1}(x_{10}, x_{20})(x_1 - x_{10}) + \frac{\partial f}{\partial x_2}(x_{10}, x_{20})(x_2 - x_{20}) + ... \] 对于n元函数，泰勒展开式可写成矩阵形式，其中包含了各阶偏导数的信息。 掌握这些数学工具对于进行机械优化设计至关重要，因为它们能帮助工程师理解和预测设计参数的微小变化对系统整体性能的影响，从而做出最佳决策。在实际工程应用中，这些理论常被用于结构分析、材料选择、能量优化等方面，确保设计的高效性和经济性。