工学插值法PPT学习教案.pptx

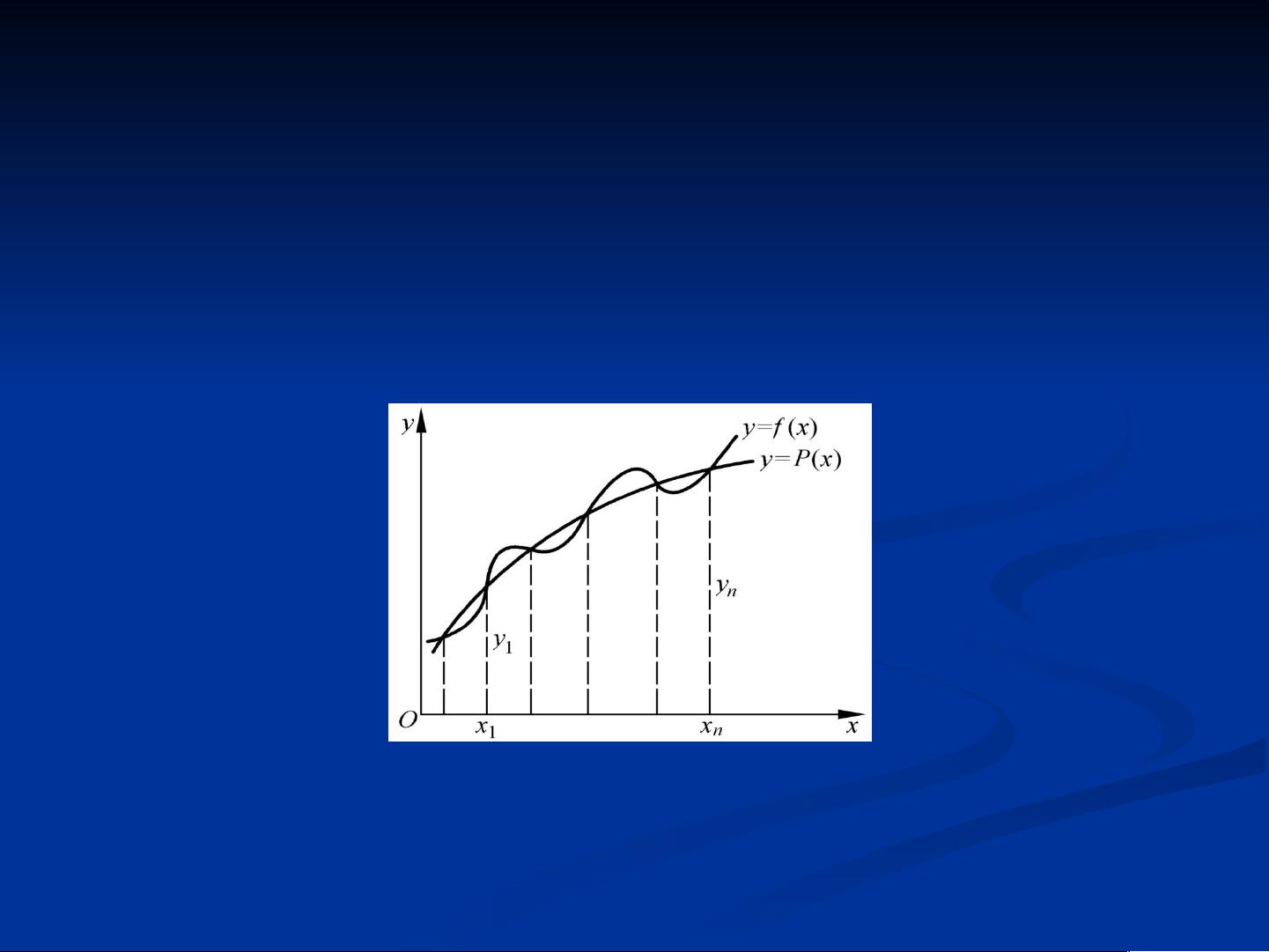
工学插值法是数值分析中的一个重要概念，用于构建数学函数来近似复杂的数据点集。这种方法在工程、科学计算以及数据分析等领域广泛应用。插值法的基本思想是找到一个函数，这个函数在给定的一系列离散点上的值与实际数据完全匹配。在本PPT学习教案中，主要介绍了几种常见的插值方法。 插值问题的提出是基于一个假设：给定一个函数f(x)，在特定的区间[a, b]上有定义，并在n+1个点x₀, x₁, ..., xn上的值y₀, y₁, ..., yn已知。目标是找到一个次数不超过n的代数多项式P(x)，使得P(xi) = yi，对于i = 0, 1, ..., n。如果找到这样的多项式P(x)，则称P(x)为f(x)的插值多项式，x₀, x₁, ..., xn为插值节点。 Lagrange插值是插值法的一种，它通过构造Lagrange基多项式来构建插值多项式。对于给定的n+1个插值点，可以得到n+1个Lagrange基多项式Li(x)，每个基多项式仅在对应的一个插值点上为1，其他点上为0。Lagrange插值多项式P(x)就是这些基多项式的线性组合，即P(x) = ∑(yi * Li(x))，i=0到n。例如，线性插值（也称为两点插值）就是最简单的Lagrange插值，它通过两点确定一条直线，适用于n=1的情况。 Newton插值和均差插值是另一种插值方法，它们基于节点处函数的导数值或差商来构建插值多项式。Newton插值公式利用了节点处的函数值和前一阶的差商，而均差插值则是通过平均差的线性组合实现插值。 Hermite插值考虑了函数值和导数值的信息，适用于需要精确捕捉函数曲率的场合。分段低次插值则是将插值问题分解为多个较小区间上的低次插值问题，每个小区间内的插值多项式可能不同，但整体保证连续性。 三次样条插值是一种特殊的分段插值方法，它在每个子区间上使用三次多项式，保证了函数在节点处的值、一阶导数和二阶导数的连续性，从而提供了更平滑的插值曲线。 在实际应用中，插值法的目的是找到一个尽可能简单的函数来逼近复杂的原始数据，同时考虑插值函数的光滑性、误差控制等因素。插值多项式的存在唯一性由Vandermonde行列式保证，当插值节点不同时，该行列式非零，表明解是唯一的。此外，还会探讨插值多项式的收敛性和误差估计，这些都是衡量插值效果的重要指标。 工学插值法是一种强大的工具，它能够帮助我们用简洁的数学形式描述复杂的数据，对数据进行分析和预测。通过理解并熟练掌握各种插值方法，可以在处理实际问题时提供有力的理论支持。