woshifafuge
- 粉丝: 8
- 资源: 58万+
最新资源
- Labview多列列表框操作框架,JKI+队列状态机,带一些OOP,扩展性强,具体看下图
- 移动机器人动态避障仿真,DWA方法,包含静态障碍物和动态障碍物,实现对障碍物避障的路径规划
- 基于stm32芯片仿真的倒车测距提示系统 包含演示视频 报告 proteus仿真 keil代码 以stm32为最小系统电路进行连接,按钮控制系统开关,使用SRF04采集倒车,LM016L液晶显示屏显示
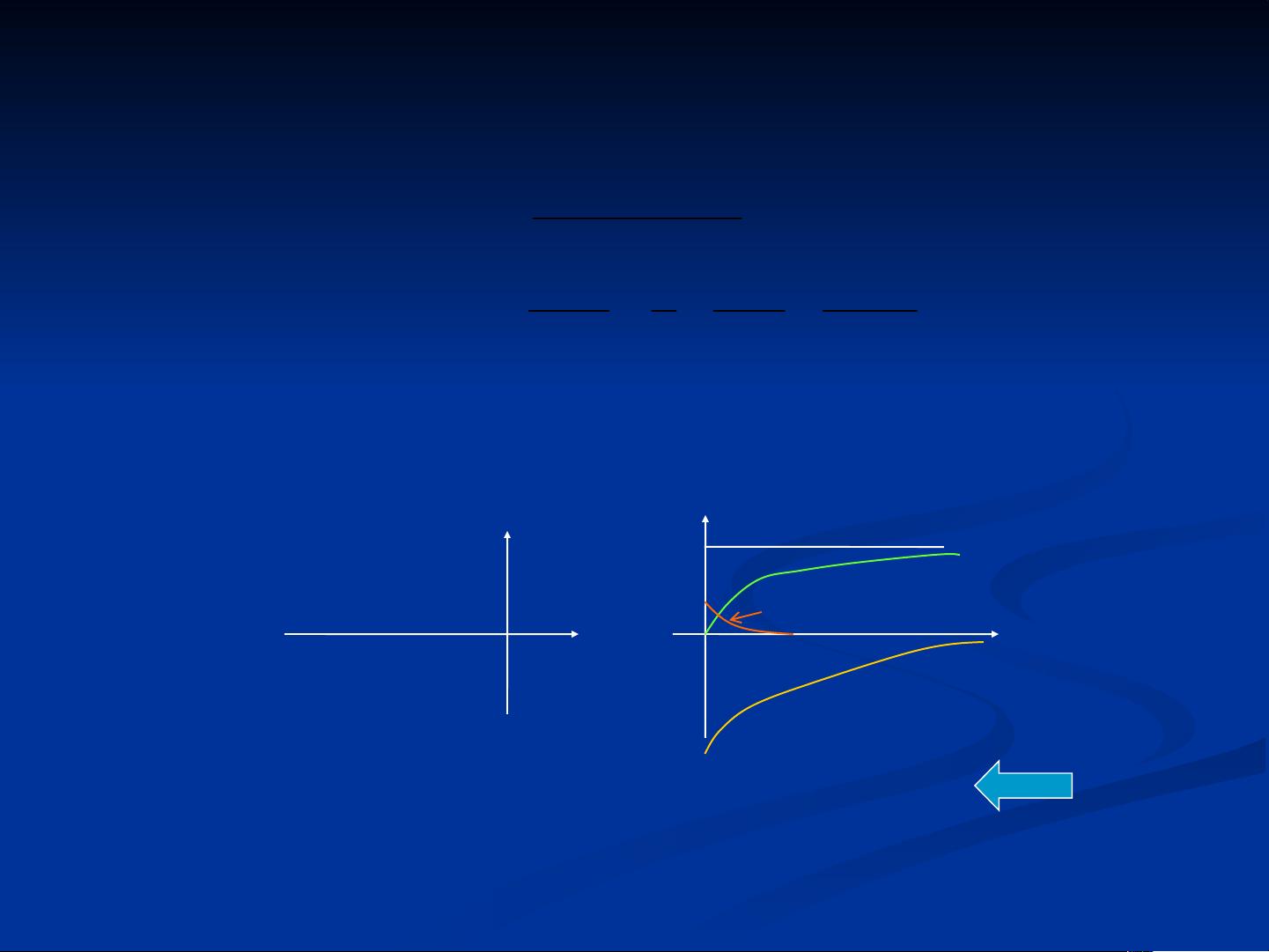
- 魔术公式轮胎模型,m文件,magic formula 可供参考
- Matlab代码:含热网的综合能源系统(IES)优化运行 风电、光伏、CHP机组(燃气燃煤)、燃气锅炉、火力发电机组,吸收式制冷机、电制冷机、蓄电池,蓄热罐等设备 负荷类型:冷、热、电 优化目标:IE
- 昆仑通泰mcgs触摸屏和台达VFD-M变频器和天正变频器的rtu通讯示例硬件:mcgs触摸屏(没屏电脑也可实现),台达vfd-m变频器
- MATLAB环境下一种基于机器学习(霍特林统计量,高斯混合模型,支持向量机)的工业数据异常检测 算法运行环境为MATLAB R2021B,执行基于机器学习(霍特林统计量,高斯混合模型,支持向量机)的
- 基于自适应滑膜观测器的轮胎力估计,可估计纵向轮胎力和侧向轮胎力,估计的结果比dugoff轮胎模型计算轮胎力的精度更高 基于分布式驱动电动汽车的车辆状态估计,分别采用无迹卡尔曼,容积卡尔曼进行估计,可
- 电钻方案,电扳手方案,低速力矩保持,堵转不停,脉冲注入 IPD初始位置检测,无刷电机控制方案,BLDC控制器,电动工具开发套件 含有脉冲注入检测位置,具备电感法 含有过温保护,过流保护,欠压保护等
- 51单片机开发的8层电梯项目,定时模拟版,包括程序源码和protues仿真,程序源码注释详细,非常适合单片机开发人员
- 威纶通MODBUS控制两台台达变频器通讯程序 ~ 可以通过触摸屏控制变频器正反转,运行停止,还能监视变频器的运行频率,输出频率,输出电压,输出电流以及转速 有做笔记,详细内容见笔记 EB8000
- DAB双有源全桥MATLAB双闭环移相ZVS 高频隔离DC DC变器模型(DAB-双有源全桥),基于MATLAB Simulink建模仿真 电压电流双闭环控制,功率双向流动,ZVS软开关 仿真模型
- carsim-simulink联合仿真,ACC自动巡航跟随 在simulink搭建控制策略,上下层分层控制 包含安全距离模型,逆发动机模型,逆制动模型,制动 驱动策略切模块,cpar文件,simf
- soc基于Matlab Simulink实现了以下功能,搭建了储能系统变模型以及钒液流电池模型,仿真效果较好,系统充放电正常 下图为系统模型图,电池输出电压电流以及SOC波形 1.钒液流电池本体建
- Webots 12自由度四足robot仿真模型 四条独立运动的腿,单腿含有三个自由度,每个自由度包含一个电机和一个电机编码器,可以像舵机一样使用位置控制,也可结合编码器使用力矩 单腿的足端包含一个
- 英威腾GD300驱动板IO板主控板方案资料原理图 英威腾变频器GD300量产方案 程序源码 主控板、驱动板、IO板 原理图 PCB bom 工艺文件,源程序
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈