PCA分析方法

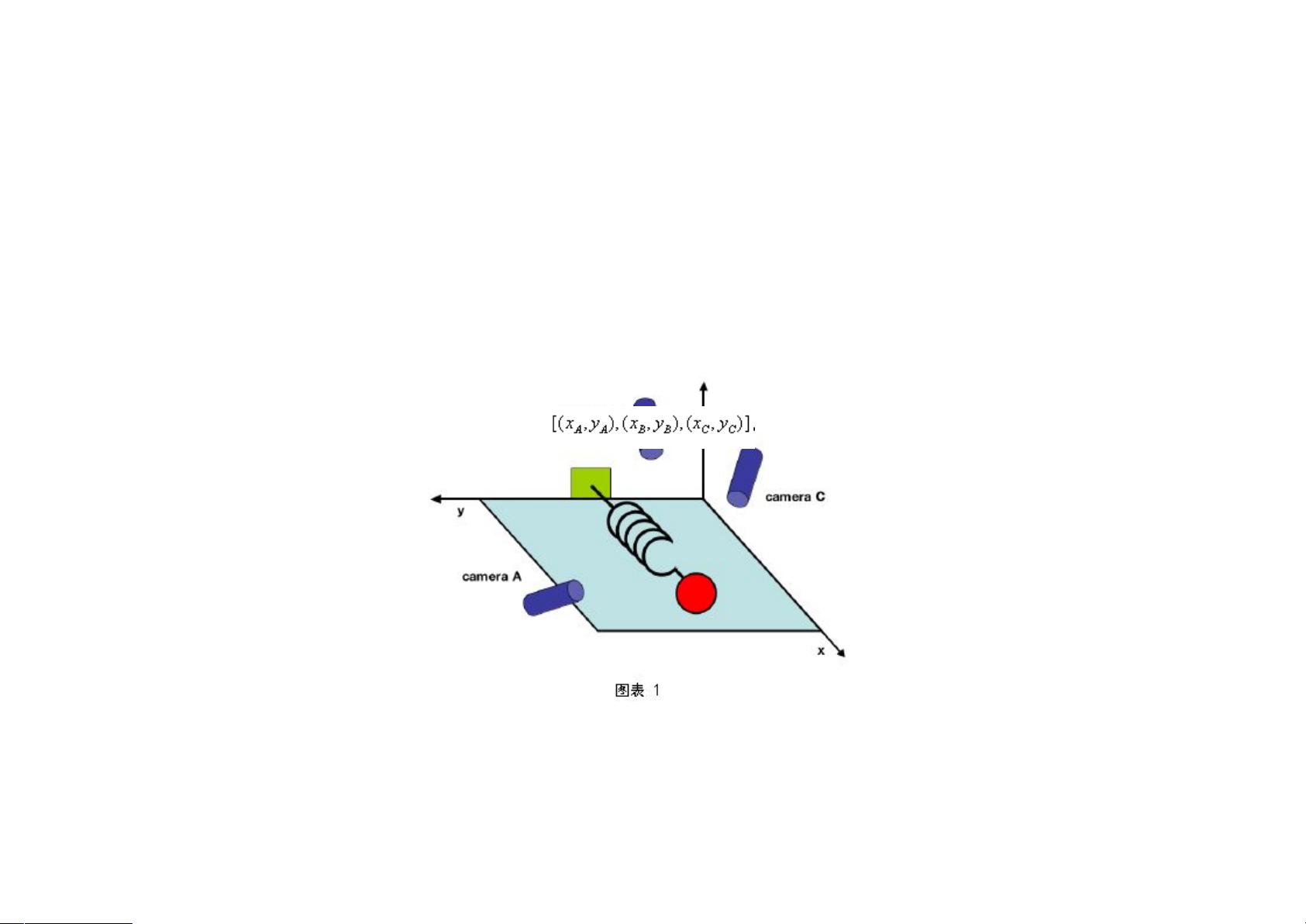
### PCA分析方法详解 #### 一、PCA简介 主元分析(Principal Component Analysis, PCA)是一种广泛应用的数据分析技术，主要用于简化原始数据集。通过PCA，我们可以有效地识别出数据中的主要特征或模式，同时减少噪音和冗余信息，从而降低数据的维度。PCA之所以受到青睐，是因为它具有操作简单且无需特定参数的优势，可以灵活地应用于多个领域，包括但不限于神经科学、计算机图形学等。 #### 二、PCA的基本原理 PCA的核心思想是寻找数据中的关键维度，这些维度能够最好地表示数据中的变化趋势。通过数学变换，可以将高维数据映射到低维空间中，同时尽可能多地保留数据中的信息。 **一个简单的模型** 以物理实验为例，假设我们正在研究一个理想弹簧系统的运动规律。该系统包含一个球体，被固定在一根理想的弹簧上。当球体沿x轴方向移动时，我们可以通过多个摄像机捕捉其运动轨迹。虽然理论上只需要记录x轴方向的位移，但在实际操作中，为了确保数据的准确性，我们通常会使用多角度的摄像机同时记录球体在三维空间中的位置。 然而，由于摄像机的角度并非完全正交，因此记录下来的每一帧图像都包含了额外的信息，这些信息在数据分析时可能会被视为冗余。此外，由于各种因素（如空气阻力、摄像机精度等）的存在，数据中还会包含一定程度的噪音。因此，我们需要一种方法来消除冗余和噪音，提取出球体真实运动的方向，即x轴。 #### 三、PCA的数学基础：基变换 在数学上，PCA的目标是通过基变换来重新描述数据空间，使得新的坐标系更好地反映了数据之间的关系。在本例中，沿着x轴的运动是最重要的，因此x轴就是我们所说的“主元”。 ##### A. 标准正交基 为了更精确地理解PCA的过程，我们需要明确数据的具体形式。在实验过程中，每个摄像机在每一个采样时间点记录了一组二维坐标，这意味着在每个时间点上，我们可以得到一个六维的列向量来表示球体的位置： \[ X = \begin{bmatrix} x_1 \\ y_1 \\ x_2 \\ y_2 \\ x_3 \\ y_3 \end{bmatrix} \] 其中，\(x_i\) 和 \(y_i\) 分别表示第i个摄像机记录的二维坐标。如果假设我们采集了N个时间点的数据，则可以构建一个\(6 \times N\)的矩阵来表示整个数据集。 #### 四、PCA的数学推导 PCA的具体步骤如下： 1. **数据标准化**：首先对数据进行标准化处理，确保各特征具有相同的尺度。 2. **计算协方差矩阵**：利用标准化后的数据计算协方差矩阵。 3. **求解特征值和特征向量**：对协方差矩阵进行特征值分解，得到特征值及其对应的特征向量。 4. **选择主成分**：根据特征值的大小选择前k个最大的特征值对应的特征向量作为新的基向量，这些基向量即为“主元”。 5. **数据转换**：使用选定的特征向量对原始数据进行线性变换，从而获得降维后的数据。 #### 五、PCA与SVD的关系 PCA与奇异值分解(Singular Value Decomposition, SVD)之间存在紧密的联系。实际上，通过对数据矩阵进行SVD分解，可以直接获得PCA所需的特征向量和特征值。这种联系使得PCA在实际应用中更加高效和简便。 #### 六、PCA的应用实例 PCA广泛应用于多种场景，例如： - **图像压缩**：通过减少图像中的颜色或像素信息来降低存储需求。 - **生物信息学**：分析基因表达数据，识别重要的基因组合。 - **金融分析**：识别股票价格波动的主要趋势。 - **市场调研**：简化客户满意度调查数据，提取关键因素。 #### 七、结论 PCA是一种强大的工具，可以帮助我们从复杂的高维数据中提取有用的信息，同时去除不必要的冗余和噪音。通过理解和掌握PCA的基本原理和应用，我们可以更有效地进行数据分析和决策支持。无论是科学研究还是商业应用，PCA都发挥着不可或缺的作用。