SAS系统讲义-主成份分析.doc

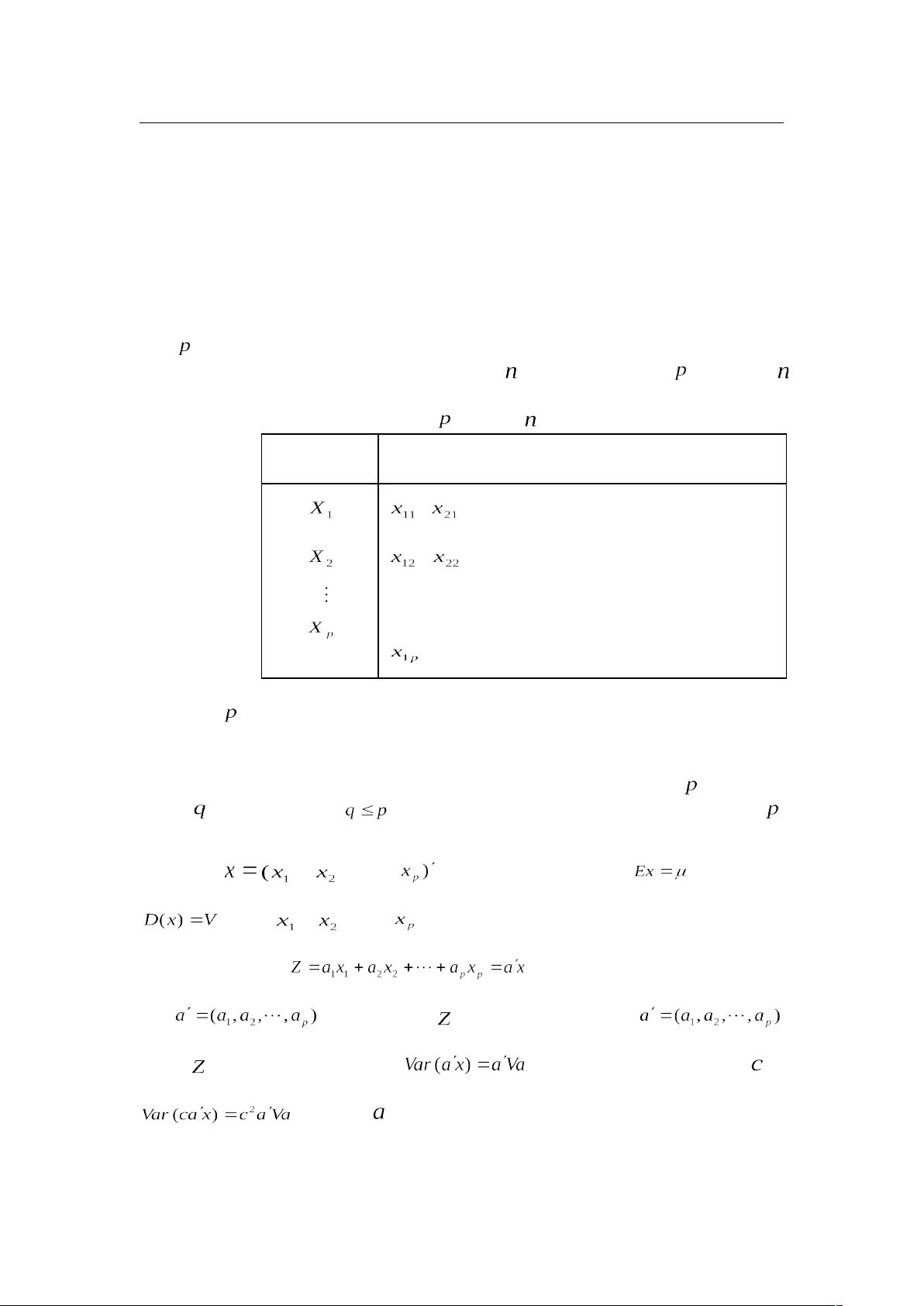
【主成份分析（PCA）详解】 主成份分析（PCA）是一种经典的统计方法，最早由皮尔逊（1901）提出，后由霍特林（Hotelling, 1933）进一步发展。该方法的主要目标是通过降维技术，将原始数据中的多个变量转化为少数几个线性组合，即主成份，这些主成份相互独立，同时最大化保留原始变量的变异信息。PCA在商务数据分析和电子商务领域有广泛应用，尤其在处理多维度数据时，能够简化复杂性，提高分析效率。 PCA的核心思想是找到一组系数，使得这些新构建的主成份具有最大的方差，从而最大化保留原始数据的信息。假设有一组包含n个变量的数据，共有m个样品。这些变量可能相互关联，导致在高维空间中分析数据时遇到困难。PCA的目标是通过线性变换，将这n个变量转化为m个新的主成份，这些主成份间互不相关，且能最大程度地反映原始数据的差异。 线性变换通常由以下公式表示： (35.1) 其中， 是原始变量的线性组合， 是一组系数。 为了使得组合后的主成份具有最大的方差，我们需要找到这组系数，使得 的方差最大。然而，如果不加限制，这个问题没有唯一解。因此，我们通常限定 ，并寻找使得协方差矩阵 的最大特征值（最大特征根），以及对应的特征向量。 协方差矩阵Σ的特征值 和特征向量 表示了数据的固有特性。非零特征值所对应的特征向量成为主成份，第i个主成份对应于协方差矩阵的第i大特征值。如果特征值非零，那么主成份之间是不相关的（35.3）。 PCA的过程主要包括以下几个步骤： 1. 计算样本的均值，使得数据中心化。 2. 构建协方差矩阵 或者相关矩阵。 3. 求解协方差矩阵的特征值和特征向量。 4. 选取最大的k个特征值，对应的特征向量作为主成份的方向。 5. 将原始数据投影到由这k个特征向量构建的新坐标系中，形成主成份。 在几何意义上，主成份是原始数据在不同方向上的最大变异方向。以二维随机向量为例，第一个主成份代表数据点沿最大变异方向的分布，而第二个主成份则是在与第一个主成份正交的方向上具有最大方差的方向。 PCA在商务数据分析中的应用包括： - 数据压缩：减少存储和计算的需求，尤其是在大数据环境下。 - 数据可视化：将高维数据降至二维或三维，便于直观理解。 - 特征选择：用于机器学习模型的预处理，降低过拟合风险，提升模型性能。 - 异常检测：主成份可以突出异常值，帮助识别数据集中的异常现象。 需要注意的是，PCA不同于最小二乘法，后者主要解决线性回归中的拟合问题，而PCA关注的是数据的内在结构和变异信息。在进行PCA时，应确保数据的质量，如无缺失值，无异常值，以及数据的正态性和线性关系的合理性，这样才能得到更准确的结果。