通信受限的多智能体系统二分实用一致性.docx

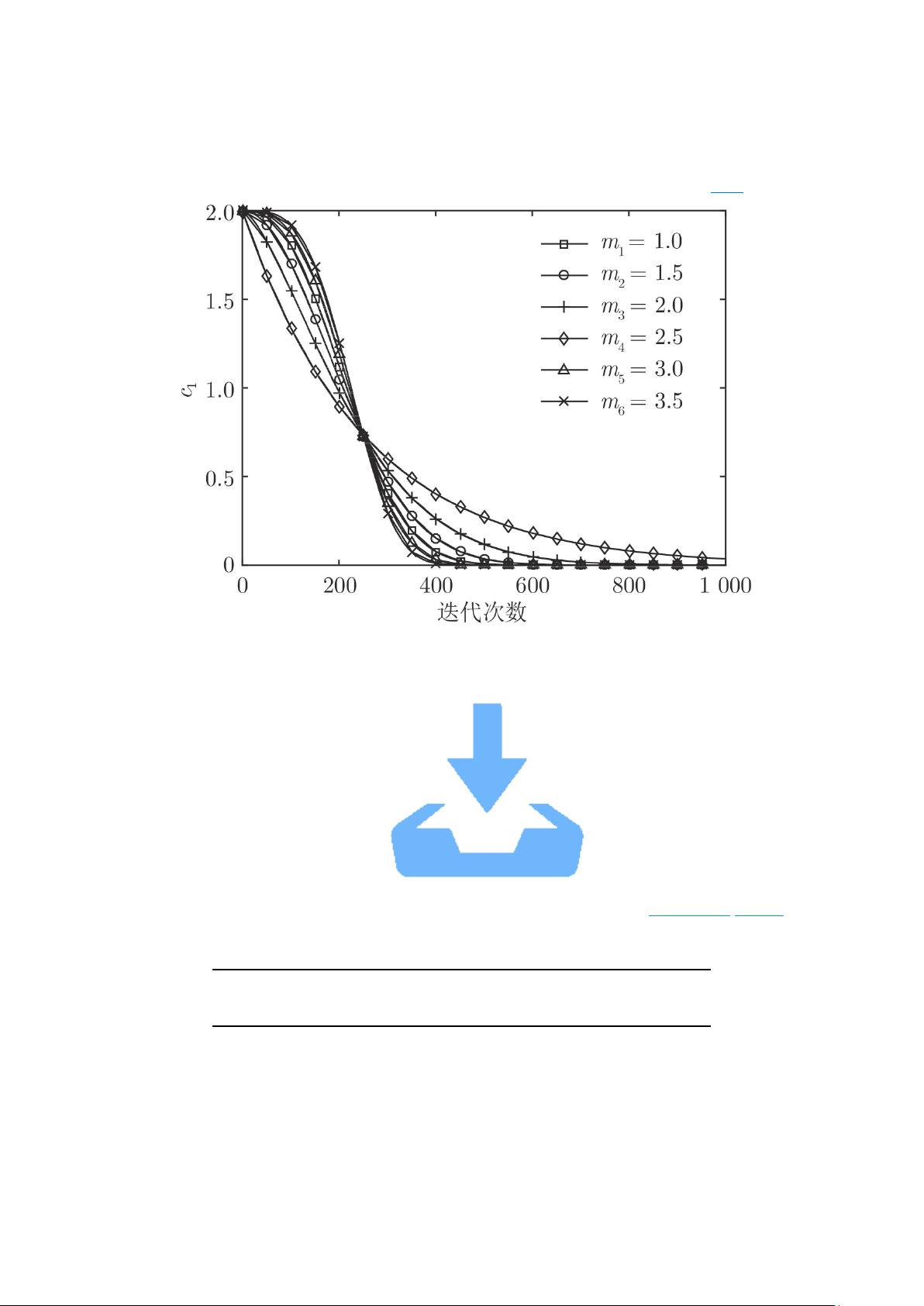
《通信受限的多智能体系统二分实用一致性》这篇文档主要探讨了在多智能体系统中，面对通信约束条件下的二分实用一致性问题，并引入了元启发式算法作为解决此类问题的有效工具。元启发式算法源于生物行为和自然现象，旨在通过随机性和局部搜索的平衡来优化搜索过程。以下是对该文核心内容的详细阐述： 文章提到了几种常见的元启发式算法，如粒子群优化（PSO）、正弦余弦算法（SCA）、蝴蝶优化算法（BOA）、飞蛾扑火优化算法（MFO）、大红斑蝶优化算法（MBO）、蚯蚓优化算法、大象放牧优化（EHO）等。这些算法在各个科学领域，包括过程控制、生物医学信号处理、图像处理等都有广泛应用。其中，樽海鞘群算法（SSA）是一种新兴的智能算法，以其简单的结构、较少的参数和易实现性受到关注。 樽海鞘群算法的核心是通过领导者和追随者的动态交互来寻找最优解。初始化种群时，每个个体的位置随机分布在设定的上界和下界之间。领导者位于群体前方，其位置更新受食物源（全局最优解）的影响，而追随者的位置更新则依赖于领导者和自身的位置。领导者的位置更新公式中，参数c1是一个关键因素，它在迭代过程中自适应降低，以平衡算法的探索和开发能力。 为了改进樽海鞘群算法的性能，文献提出了多种策略。例如，固定惯性权重可以加速算法的收敛速度；混沌樽海鞘群算法利用混沌理论来发现最优特征子集，提高分类精度；子群规模调整策略让每个子种群在进化过程中逐渐增大，以提升初期探索和后期开采能力；共享机制的引入降低搜索盲目性，加快收敛速度；非均匀变异演化算法避免局部最优，防止早熟；高斯变异则增强了种群多样性。 针对樽海鞘群算法的求解精度和收敛速度问题，本文提出了多子群的共生非均匀高斯变异樽海鞘群算法（MSNSSA）。该算法将种群划分为领导者、追随者和链尾者三个子群，分别采取不同的更新策略：领导者通过分析参数c1来平衡探索与开发；追随者应用共生策略，增强与最优个体的交流；链尾者则利用非均匀高斯变异增加种群多样性。通过对比14个典型测试函数和CEC 2014测试函数的结果，验证了MSNSSA的有效性和鲁棒性。 本文深入研究了通信受限的多智能体系统中的二分实用一致性问题，通过对樽海鞘群算法的改进，提高了求解精度和收敛速度。这些改进策略对于优化问题的解决具有重要意义，也为未来多智能体系统的研究提供了新的思路和方法。