"如何检验数据是否属于正态分布"
正态分布是概率论和统计学中最重要的概念之一,对于数据分析和模型建立具有重要影响。检验数据是否属于正态分布是数据分析的第一步骤,本文将介绍两种检验方法来确定数据是否属于正态分布。
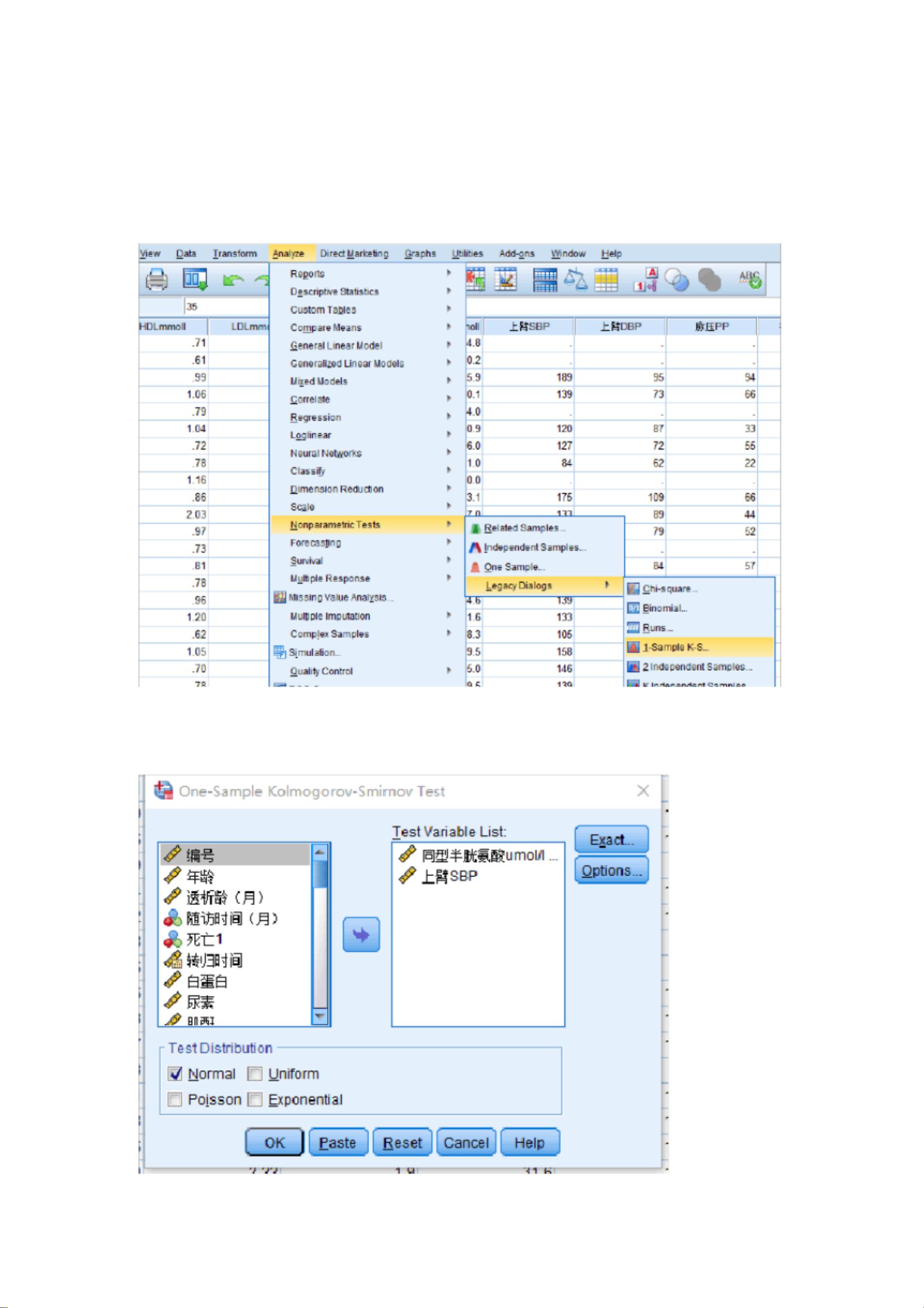
检验方法一:Kolmogorov-Smirnov Test(K-S检验)
K-S检验是一种非参数检验方法,用于检验数据是否符合正态分布。该方法的优点是可以处理小样本数据,并且不需要假设数据的分布形式。在SPSS中,可以通过以下步骤进行K-S检验:
1. 选择Analysis → Nonparametric → Legacy Dialogs → 1-Sample K-S
2. 在Test variable List中选择要分析的数据
3. 选择Option,可以计算数据的均值和四分位数
4. 结果输出P>0.05,说明数据与正态分布无显著差异,即数据符合正态分布。
检验方法二:Explore
Explore是一种描述性统计方法,用于描述数据的分布情况。在SPSS中,可以通过以下步骤进行Explore:
1. 选择Analysis → Descriptive Statistics → Explore
2. 选择需要验证的因变量(Dependent List)
3. 在Plots中勾选Normality plots with tests
4. 结果输出包括Mean±Std.、Skewness和Kurtosis三个指标。
其中,Skewness(偏度)越趋近于0,数据越服从正态分布;Skewness>0,为正偏态或左偏;Skewness<0,为负偏态或右偏。Kurtosis(峰度)越趋近于3,数据越服从正态分布;Kurtosis>3,峰度尖锐;Kurtosis<3,峰度扁平。
结果解释
结果输出包括两部分:一是KS检验和SW检验的检验结果,二是数据的描述性统计结果。当P>0.05时,可以认为数据是呈正态分布的。在小样本时,关注SW检验的检验结果;在大样本时,关注KS检验的检验结果。
检验数据是否属于正态分布是数据分析的关键步骤,通过K-S检验和Explore两种方法可以确定数据是否符合正态分布。本文为读者提供了两种检验方法的详细步骤和结果解释,旨在帮助读者更好地理解和应用正态分布的概念。