数值分析实验报告.doc（含源码）

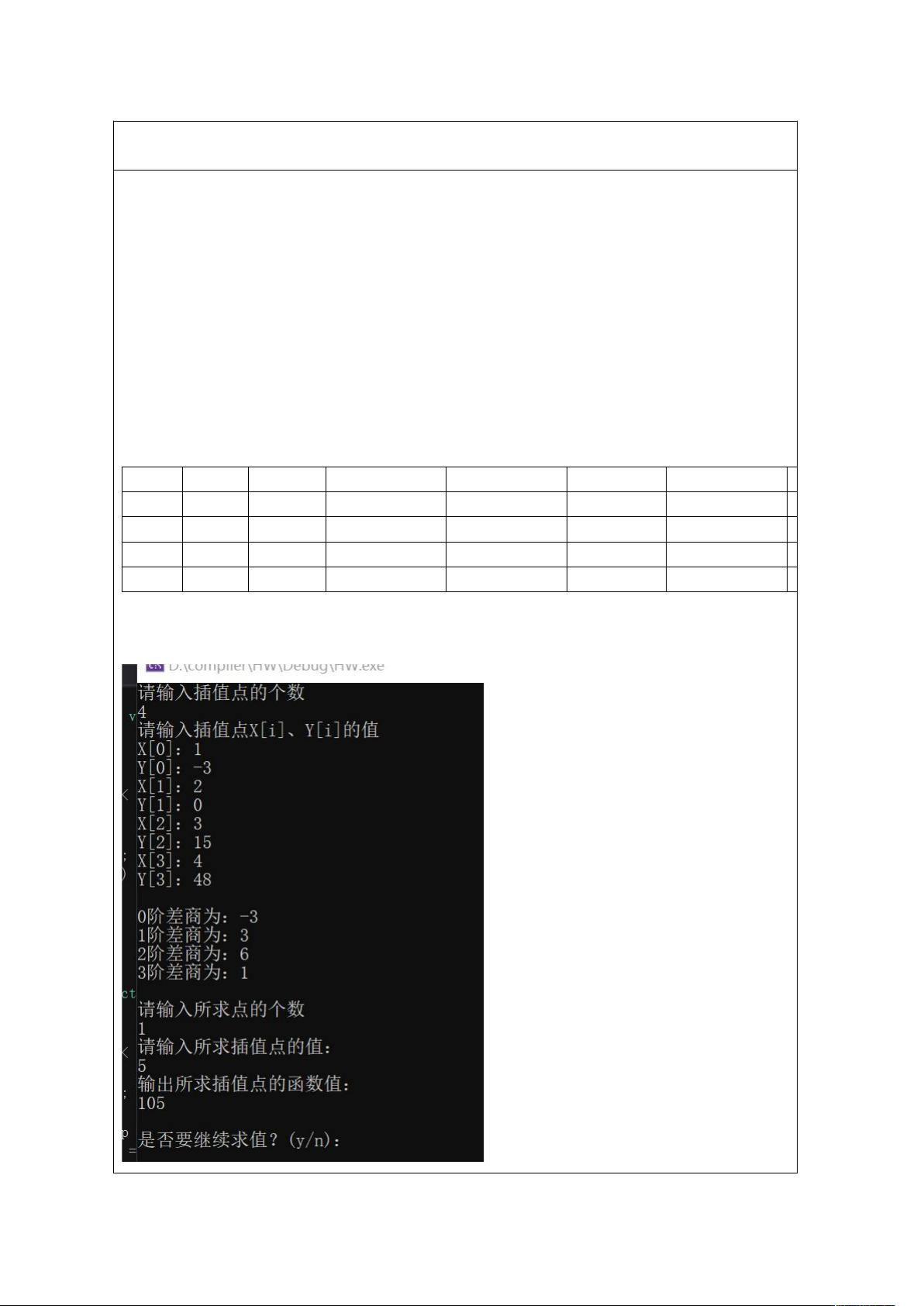
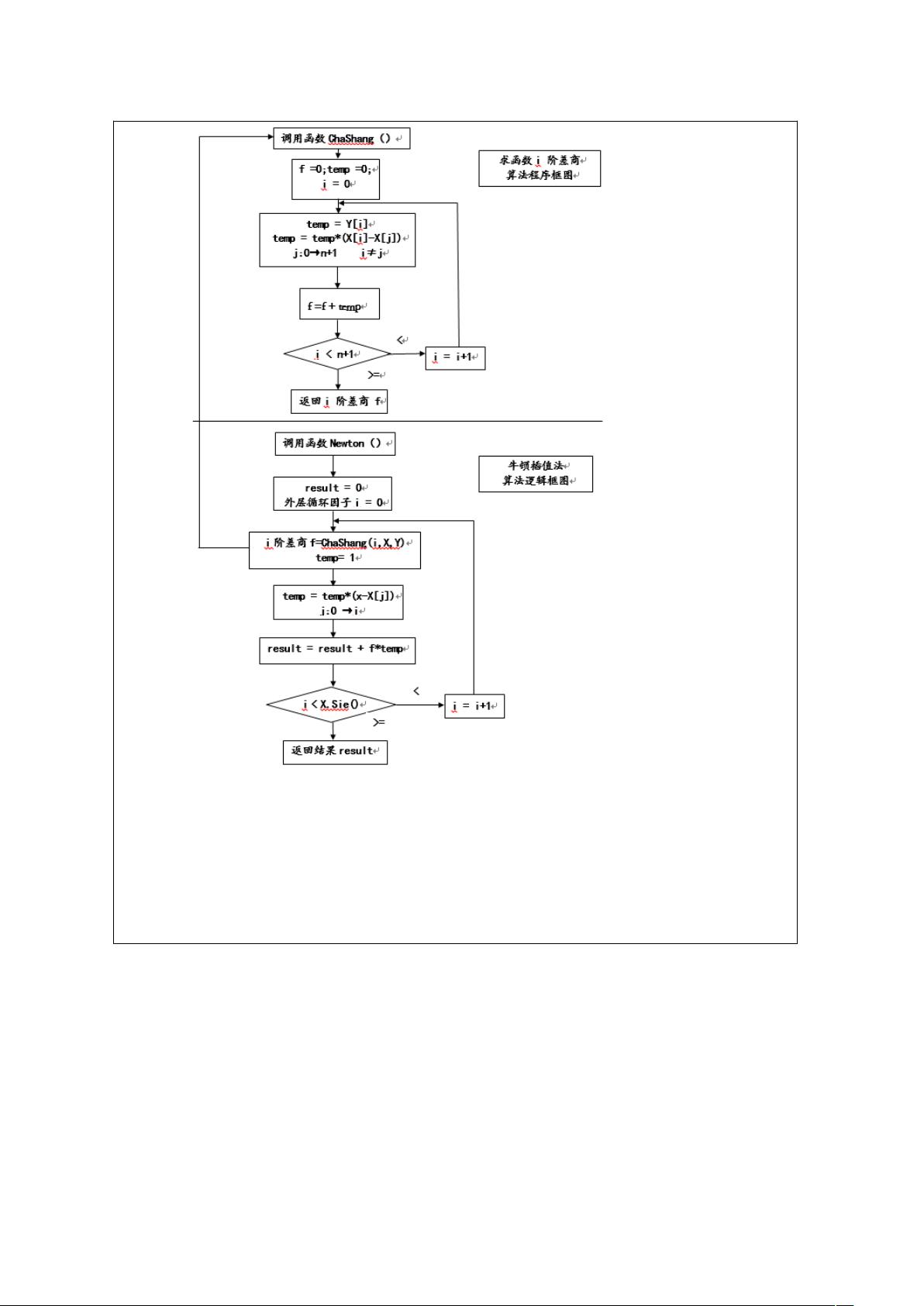
【数值分析实验报告】 实验课程名称：数值分析 实验项目名称：用C语言实现几个多项式插值的程序 实验目的： 本实验旨在通过C语言编程实现数值分析中的多项式插值方法，包括牛顿插值法，以及常微分方程初值问题的求解，非线性方程求根和线性方程组的解法。这些方法在科学计算中具有广泛的应用，例如数据拟合、物理模型的模拟和工程问题的求解。 一、多项式插值： 1. 牛顿插值法：牛顿插值法是一种通过差商来构建多项式的方法。当给定n个插值点(x_i, y_i)，可以构造一个n-1次多项式P(x)使得P(x_i)=y_i。在C语言中，通过嵌套循环计算差商，然后将差商代入牛顿插值公式中求解。 实验方案设计： (1) 输入插值点的个数n，以及n个插值点的坐标(x_i, y_i)。 (2) 计算差商，存储在数组中。 (3) 利用差商和循环计算给定插值点x_p处的函数值P(x_p)。 实验手段： 使用Visual Studio (2019)作为开发环境，以C语言编写代码，实现牛顿插值法。 调试方法： 通过设置断点，观察变量的值是否正确，确保程序按预期执行。 二、常微分方程初值问题求解： 实验未提供具体实现，但通常可以采用龙格-库塔方法、欧拉方法等数值方法求解。 三、非线性方程求根： 常见的方法有牛顿迭代法、二分法、梯形法等，需要迭代逼近零点。 四、线性方程组的解： 可以使用高斯消元法、克拉默法则或LU分解等方法。 实验总结： 通过实验，学生能够熟练掌握C语言编程，尤其是数组和循环结构的运用。同时，对数值分析中的多项式插值、微分方程求解、非线性方程求根和线性方程组的解法有深入理解。实验锻炼了编程思维，提高了问题解决能力。 源码部分略。 实验的挑战在于理解和应用数值方法，以及处理可能的误差和精度问题。实验结果表明，程序能正确执行，无异常现象，对于不同插值点和阶数的差商，都能得出理想的结果。未来的学习中，应继续提升编程技巧，优化代码效率，提高程序的可读性和可维护性。