• The goal is to efficiently explore the search space in
order to find (close to) optimal solutions.
• Meta-heuristics are not problem-special.
• The basic concepts of meta-heuristics permit an abstract
level of description.
• Meta-heuristic algorithms are approximate and gener-
ally nondeterministic.
• One of the common disadvantages in these methods is
the difficulty of adjusting and matching of parameters.
Different criteria are used to classify meta-heuristic
algorithms (Talbi 2009). In general, meta-heuristic algo-
rithms are divided into two categories: one-solution-based
algorithms and population-based algorithms (Boussaı
¨
d
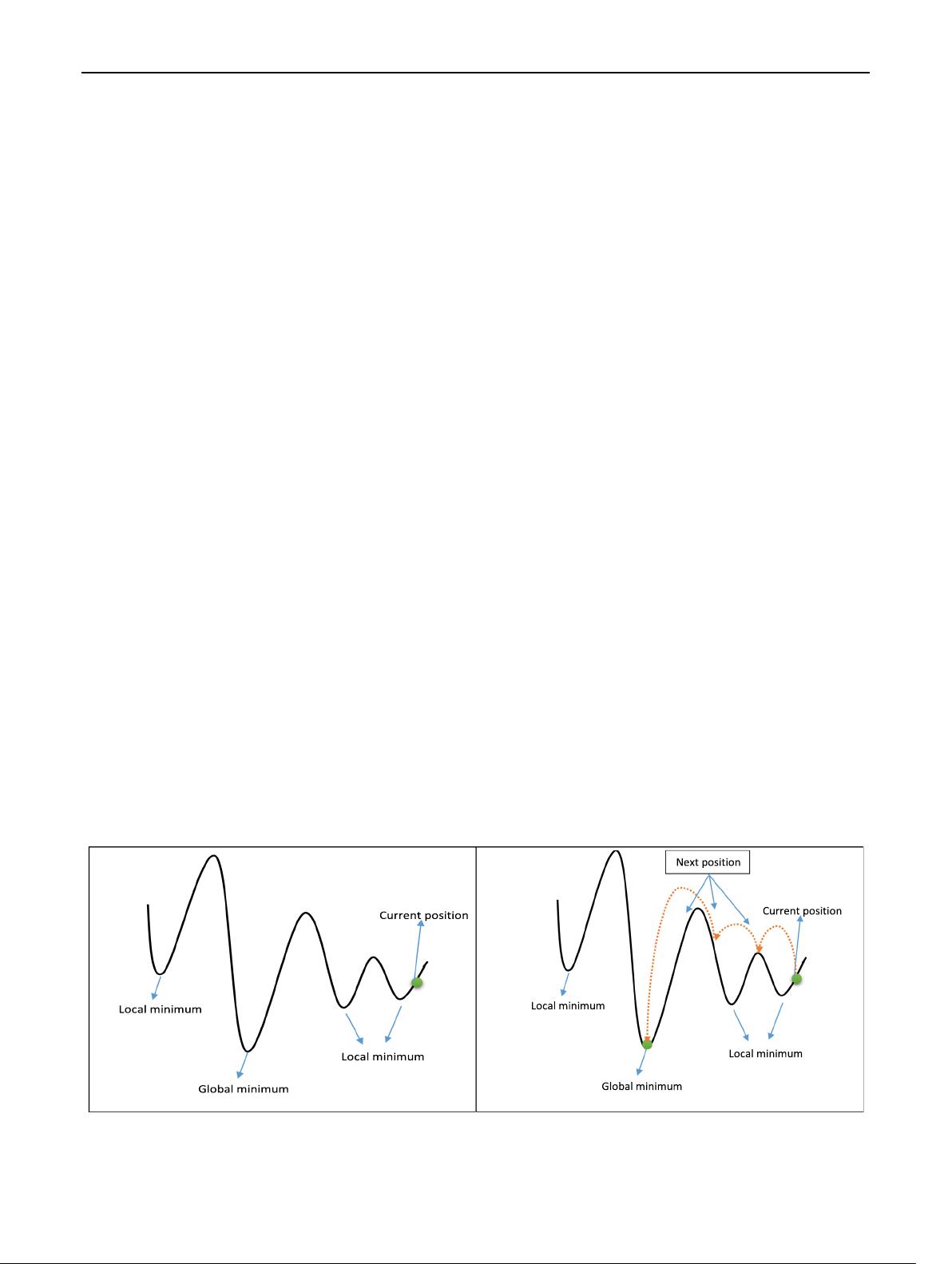
et al. 2013). A one-solution-based algorithm changes a
solution during the search process (Fig. 1), whereas in the
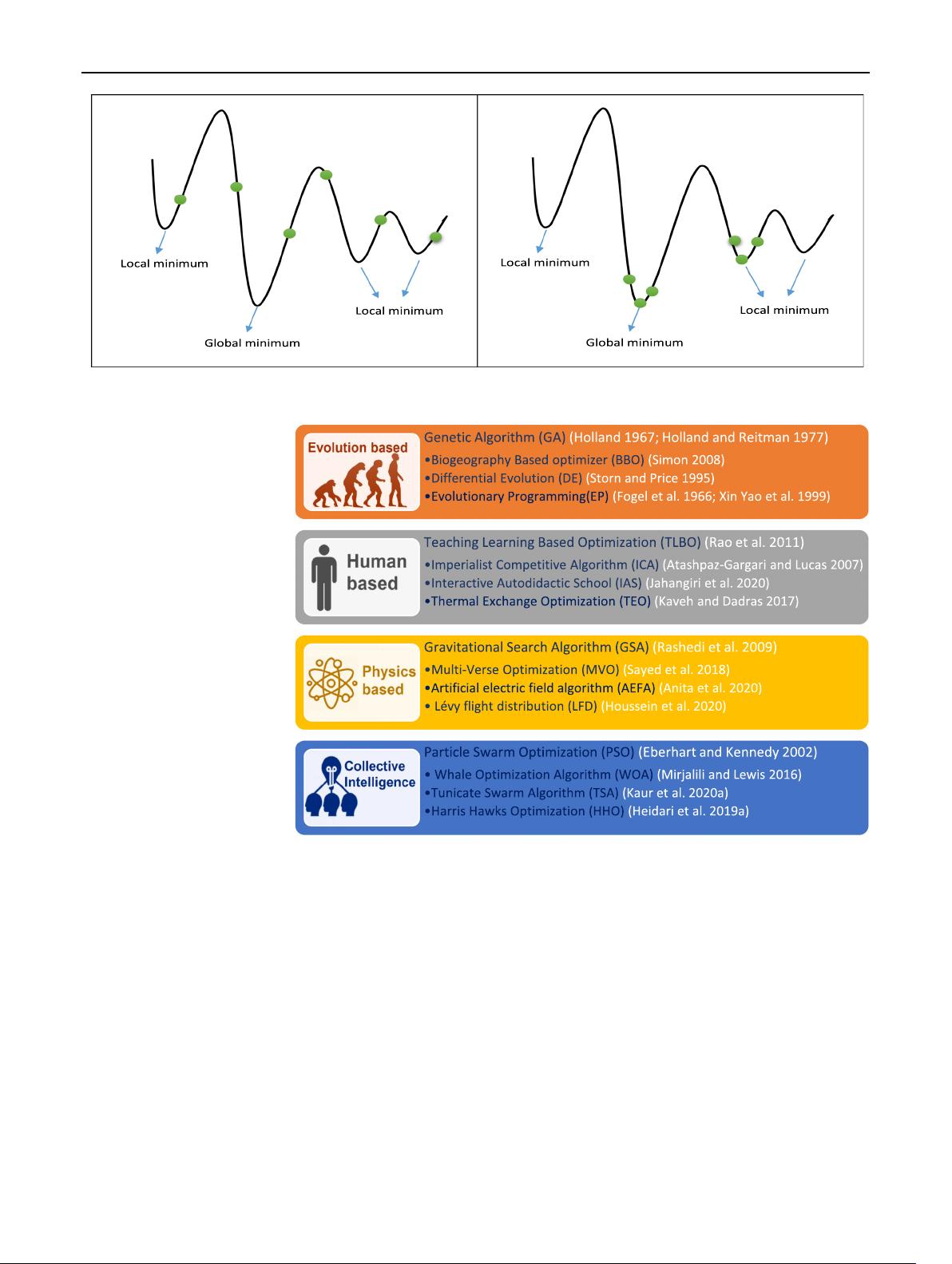
population-based algorithms, a population of solutions is
considered (Fig. 2). The characteristics of these two types
of algorithms are complementary to each other. One-so-
lution-based meta-heuristic algorithms can focus on local
search areas. In contrast, population-based meta-heuristic
algorithms can lead the search to different solution space
regions (Zhou et al. 2011).
Population-based optimization methods are inspired by
human phenomena, collective intelligence, evolutionary
concepts and physical phenomena (Shen et al. 2016; Wang
et al. 2017; Zhang et al. 2018; Rizk-Allah 2018). Many
studies have tried to classify optimization algorithms based
on their type of inspiration. Figure 3 shows a type of this
classification. The algorithms start with a random initial
population (Heidari et al. 2017; Mafarja et al. 2018a), and
this population is directed to the optimal areas in the search
space by search mechanisms (Aljarah et al. 2018; Mafarja
et al. 2018b). The search process involves two stages of
exploration and exploitation. The well-designed algorithm
and enriched random nature should explore different parts
of the search space at the exploration stage. The
exploitation stage is usually performed after the explo-
ration phase. The algorithm focuses on good solutions and
improves the search operation by searching around these
right solutions in this stage. A good algorithm should
balance the two steps to prevent premature convergence or
belated convergence. The structure of optimization algo-
rithms is almost similar, and their main difference is in how
the exploration and exploitation phases are performed.
How to balance the exploration and operation phases is
another indicator that differentiates the performance of
algorithms.
2 Related works
This section introduces a number of popular optimization
algorithms. These methods include genetic algorithms
(GA) (Holland 1967; Holland and Reitman 1977), evolu-
tionary programming(EP) (Fogel et al. 1966; Xin Yao et al.
1999), particle swarm optimization (PSO) (Eberhart and
Kennedy 2002), ant colony optimization (ACO) (Colorni
et al. 1991), differential evolution (DE) (Storn and Price
1995) and harmony search (HS) (Manjarres et al. 2013).
Although these algorithms can solve many real and chal-
lenging problems, there are still issues that these algorithms
have not been able to solve. Therefore, an algorithm can
help solve one set of problems, but it is ineffective in
another set of problems. Some of the new algorithms are
gray wolf optimizer (GWO) (Mirjalili et al. 2014), artificial
bee colony (ABC) algorithm (Basturk and Karaboga 2006),
firefly algorithm (FA) (Yang 2010), imperialist competitive
algorithm (ICA) (Atashpaz-Gargari and Lucas 2007),
cuckoo search algorithm (CS) (Yang and Suash Deb 2009;
Yang and Deb 2010; Rajabioun 2011), gravitational search
algorithm (GSA) (Rashedi et al. 2009), charged system
search (CSS) (Kaveh and Talatahari 2010), magnetic
Fig. 1 One-solution-based meta-heuristic algorithm
I. Naruei et al.
123

 捕食者算法.zip (2个子文件)
捕食者算法.zip (2个子文件)  捕猎者算法.pdf 6.73MB
捕猎者算法.pdf 6.73MB Hunter_Prey_Optimization.zip 3KB
Hunter_Prey_Optimization.zip 3KB
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功



- 1
- 2
- 3
- 4
- 5
- 6
前往页