智能优化算法：金枪鱼群优化算法tunaswarmoptimizationalgorithm

共2个文件

pdf：1个

zip：1个

版权申诉

matlab

人工智能

机器学习

群智能优化算法

5星 · 超过95%的资源 149 浏览量 2021-11-16 08:29:16 上传评论 5 收藏 5.94MB ZIP 举报

金枪鱼群优化算法（Tuna Swarm Optimization Algorithm, TSOA）是一种仿生优化算法，源于对金枪鱼群体在海洋中捕食行为的观察。该算法借鉴了金枪鱼在海洋中的群体智能，用于解决复杂的工程问题和优化任务，如函数优化、参数调优、机器学习模型的权重优化等。在本文中，我们将深入探讨TSOA的基本原理、工作流程以及其在MATLAB环境下的实现。金枪鱼群优化算法的核心思想是模仿金枪鱼在寻找猎物时的集体行为。金枪鱼具有出色的游泳速度和敏锐的感知能力，它们通过协同狩猎来提高捕食效率。TSOA将这种行为抽象为数学模型，通过模拟金枪鱼的位置更新和速度调整来搜索问题的最优解。 TSOA的工作流程主要包括以下几个步骤： 1. 初始化：随机生成一定数量的金枪鱼个体（解），每个个体代表一个可能的解决方案，其位置和速度代表了参数的取值。 2. 搜索：每个金枪鱼根据当前速度和位置更新其新的位置，同时考虑个体间的相互影响和捕食行为。 3. 更新速度：金枪鱼的速度受到自身和邻居的影响，这体现在速度更新公式中，通常包含一个探索成分和一个开发成分，以平衡全局探索和局部开发。 4. 更新位置：根据新速度，更新金枪鱼的位置。 5. 评估：计算每个金枪鱼的适应度值（fitness value），通常与目标函数相关，越小表示越优。 6. 判断停止条件：若达到预设的迭代次数或适应度阈值，结束算法，否则返回步骤2。在MATLAB环境下，实现TSOA的关键在于编写合适的函数来实现上述步骤。具体包括初始化函数、速度更新函数、位置更新函数、适应度计算函数以及主循环。在给定的压缩包中，应包含这些函数的源代码，你可以直接运行测试，验证其有效性。 TSOA作为一种群智能优化算法，与遗传算法、粒子群优化算法等有相似之处，但其独特的金枪鱼捕食行为引入了更丰富的动态特性，可能在某些问题上表现出更好的优化性能。在人工智能和机器学习领域，TSOA可以应用于模型参数的优化，如神经网络的权重和阈值调整，以提高模型的预测精度。金枪鱼群优化算法是一种创新的优化方法，它利用生物界的智慧来解决复杂问题，具有较高的灵活性和潜力。通过MATLAB实现，我们可以方便地应用TSOA到实际问题中，并根据具体需求进行算法的调整和改进。

资源推荐

资源详情

资源评论

收起资源包目录

金枪鱼群优化算法.zip （2个子文件）

金枪鱼群优化算法

Tuna_Swarm_Optimization_A_Novel_Swarm-Based_Metahe.pdf 2.85MB

Code_Tuna swarm optimization.zip 3.31MB

Review Article

Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic

Algorithm for Global Optimization

Lei Xie ,

Tong Han,

Huan Zhou ,

Zhuo-Ran Zhang,

Bo Han,

and Andi Tang

Aeronautics Engineering College, Air Force Engineering University, Xi’an 710038, China

Unit 95806 of People’s Liberation Army of China, Beijing, China

Unit 93525 of People’s Liberation Army of China, Beijing, China

Correspondence should be addressed to Andi Tang; 418932433@qq.com

Received 16 September 2021; Accepted 25 September 2021; Published 20 October 2021

Academic Editor:

Ahmed Mostafa Khalil

permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

In this paper, a novel swarm-based metaheuristic algorithm is proposed, which is called tuna swarm optimization (TSO). e

main inspiration for TSO is based on the cooperative foraging behavior of tuna swarm. e work mimics two foraging behaviors of

tuna swarm, including spiral foraging and parabolic foraging, for developing an eﬀective metaheuristic algorithm. e per-

formance of TSO is evaluated by comparison with other metaheuristics on a set of benchmark functions and several real

engineering problems. Sensitivity, scalability, robustness, and convergence analyses were used and combined with the Wilcoxon

rank-sum test and Friedman test. e simulation results show that TSO performs better compared to other

comparative algorithms.

1. Introduction

Real-world optimization problems have become more

challenging, which requires more eﬃcient solution methods.

Diﬀerent scholars have studied various approaches to solve

these complex and diﬃcult problems from the real world. A

part of researchers solve these optimization problems using

traditional methods such as quasi-Newton, conjugate gra-

dient, and sequential quadratic programming methods.

However, owing to the nonlinear, nonproductivity char-

acteristics of most real-world optimization problems and the

involvement of multiple decision variables and complex

constraints, these traditional algorithms are diﬃcult to be

solved eﬀectively [1, 2]. e metaheuristic algorithm has the

advantages of not relying on the problem model, not re-

quiring gradient information, having strong search capa-

bility and wide applicability, and can achieve a good balance

between solution quality and computational cost [3].

erefore, the metaheuristic algorithms have been proposed

to solve real-world optimization problems, such as image

segmentation [4, 5], feature selection [6, 7], mission plan-

ning [8, 9], parameter optimization [10, 11], job shop

scheduling [12, 13], etc.

Metaheuristic algorithms are usually classiﬁed into three

categories [14]: evolution-based algorithms, physical-based

algorithms, and swarm-based algorithms. e evolution-

based algorithm is inspired by the laws of evolution in

nature. Genetic algorithm (GA) [15], inspired by Darwin’s

theory of superiority and inferiority, is a well-known evo-

lution-based algorithm. With the popularity of GA, several

other widely used evolution-based algorithms have been

proposed, including diﬀerential evolution (DE) [16], genetic

programming (GP) [17], evolutionary strategies (ES) [18],

and evolutionary programming (EP) [19]. In addition,

several new evolution-based algorithms have been proposed,

such as artiﬁcial algae algorithm (AAA) [20], biogeography-

based optimization (BBO) [21], and monkey king evolu-

tionary (MKE) [22]. e physical-based algorithms are in-

spired by various laws of physics. One of the most famous

algorithms of this category is simulated annealing (SA) [23].

SA is inspired by the law of thermodynamics in which a

material is heated up and then cooled slowly. ere are other

physical-based algorithms proposed, including gravitational

search algorithm (GSA) [24], nuclear reaction optimization

(NRO) [25], water cycle algorithm (WCA) [26], and sine

cosine algorithm (SCA) [27]. e swarm-based algorithms

Hindawi

Computational Intelligence and Neuroscience

Volume 2021, Article ID 9210050, 22 pages

https://doi.org/10.1155/2021/9210050

are inspired by the social behavior of diﬀerent species in

natural groups. Particle swarm optimization (PSO) [28] and

ant colony optimization (ACO) [29] are two typical swarm-

based algorithms. PSO and ACO mimic the aggregation

behavior of bird colonies and the foraging behavior of ant

colonies, respectively. Some other algorithms of this cate-

gory include: grey wolf optimizer (GWO) [30], monarch

butterﬂy optimization (MBO) [31], elephant herding opti-

mization (EHO) [32], moth search algorithm (MSA) [33],

manta ray foraging optimization (MRFO) [34],earthworm

optimization algorithm (EOA) [35], etc. With the devel-

opment of metaheuristics, a type of human-based meta-

heuristic algorithm is also emerging. ese algorithms are

inspired by the characteristics of human activity. Teaching-

learning-based optimization (TLBO) [36], inspired by tra-

ditional teaching methods, is a typical example of this

category among metaheuristic algorithms. Other human-

based metaheuristics include: social evolution and learning

optimization (SELO) [37], group teaching optimization

algorithm (GTOA) [38], heap-based optimizer (HBO) [39],

political optimizer (PO) [40], etc.

ere is a common feature of all these metaheuristic

algorithms that rely on exploration and exploitation in the

search space to ﬁnd the optimal solution [41, 42]. Explo-

ration means that the algorithm searches for promising

regions in a wide search space and exploitation is a further

search for the best solution in the promising regions. e

balance of the two search behaviors aﬀects the quality of the

solution. When exploration dominates, exploitation de-

clines, and vice versa. erefore, it is a big challenge to

balance exploration and exploitation for metaheuristics.

Although there are constantly new algorithms being de-

veloped, the no free lunch (NFL) [43] theory states that no

particular algorithm can solve all optimization problems

perfectly. e NFL has motivated researchers to develop

eﬀective metaheuristic algorithms to solve various ﬁelds of

optimization problems.

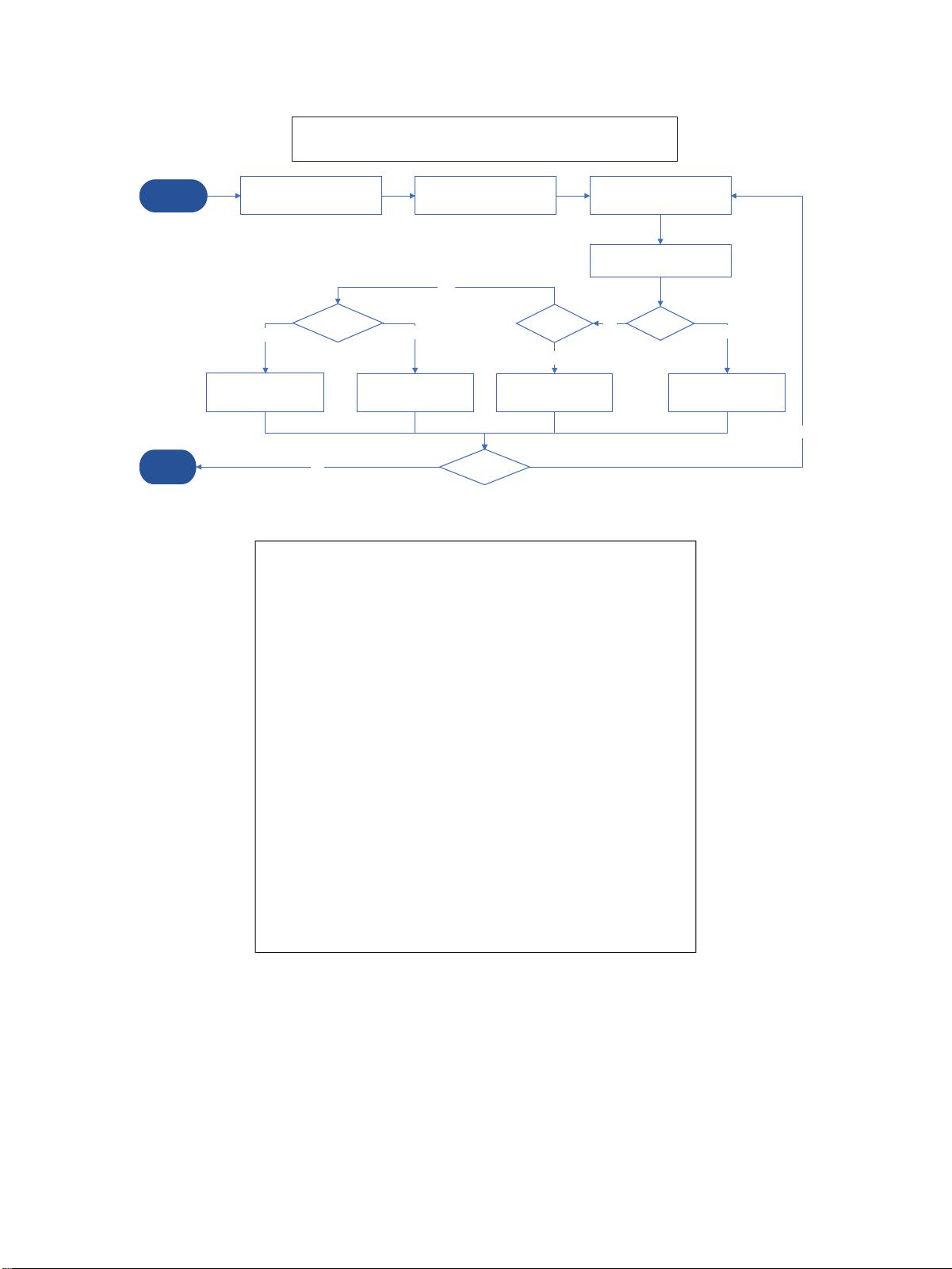
In this paper, a novel swarm-based metaheuristic is

presented called tuna swarm optimization (TSO). It is in-

spired by two types of swarm foraging behavior of tunas. e

TSO is evaluated in 23 benchmark functions and 3 engi-

neering design problems. Test results reveal that the method

proposed in this paper signiﬁcantly outperforms those

popular and recent metaheuristics. is paper is structured

as follows: Section 2 describes the inspiration for TSO and

builds the corresponding mathematical model. A bench-

mark function set and three engineering design problems are

employed to check the performance of TSO in Sections 3 and

4, respectively. Section 5 concludes the overall work and

provides an outlook for the future.

2. Tuna Swarm Optimization

2.1. Inspiration. Tuna, scientiﬁcally named unnini, is a

marine carnivorous ﬁsh. ere are many species of tuna, and

the size varies greatly. Tuna are top marine predators,

feeding on a variety of midwater and surface ﬁsh. Tunas are

continuous swimmers, and they have a unique and eﬃcient

way of swimming (called ﬁshtail shape) in which the body

stays rigid while the long, thin tail swings rapidly. Although

the single tuna swims very fast, it is still not as fast as the

nimble small ﬁsh response. erefore, the tuna will use the “

group travel “ method for predation. ey use their intel-

ligence to ﬁnd and attack their prey. ese creatures have

evolved a variety of eﬀective and intelligent foraging

strategies.

e ﬁrst strategy is spiral foraging. When tuna are

feeding, they swim by forming a spiral formation to drive

their prey into shallow water where they can be attacked

more easily.

e second strategy is parabolic foraging. Each tuna

swims after the previous individual, forming a parabolic

shape to enclose its prey.

Tuna successfully forage by the above two methods. In

this paper, a new swarm-based metaheuristic optimization

algorithm, namely, tuna swarm optimization, is proposed

based on modeling these natural foraging behaviors.

2.2. Mathematical Model. In this section, the mathematical

model of the proposed algorithm is described in detail.

2.2.1. Initialization. Similar to most swarm-based meta-

heuristics, TSO starts the process of optimization by gen-

erating initial populations at random uniformly in the search

space,

int

� rand · (ub − lb)+ lb, i � 1, 2, ..., NP,

(1)

where X

int

is the i

initial individual, ub and lb are the upper

and lower boundaries of the search space, NP is the number

of tuna populations, and rand is a uniformly distributed

random vector ranging from 0 to 1.

2.2.2. Spiral Foraging. When sardines, herring, and other

small schooling ﬁsh encounter predators, the entire school of

ﬁsh forms a dense formation constantly changing the

swimming direction, making it diﬃcult for predators to lock

a target. At this time, the tuna group chase the prey by

forming a tight spiral formation. Although most of the ﬁsh in

the school have little sense of direction, when a small group

of ﬁsh swim ﬁrmly in a certain direction, the nearby ﬁsh will

adjust their direction one after another and ﬁnally form a

large group with the same goal and start to hunt. In addition

to spiraling after their prey, schools of tuna also exchange

information with each other. Each tuna follows the previous

ﬁsh, thus enabling information sharing among neighboring

tuna. Based on the above principles, the mathematical

formula for the spiral foraging strategy is as follows:

t+1

�

· X

best

+ β · X

best

− X

􏼌

􏼐 􏼑

+ α

· X

, i � 1,

· X

best

+ β · X

best

− X

􏼌

􏼐 􏼑

+ α

· X

i− 1

, i � 2, 3, ..., NP,

⎧

⎪

⎨

⎪

⎩

(2)

� a +(1 − a) ·

max

(3)

2 Computational Intelligence and Neuroscience

�(1 − a) − (1 − a) ·

max

(4)

β � e

· cos(2πb),

(5)

l � e

3cos t

max

+1/t

( )

− 1

( )

(6)

where X

t+1

is the i

individual of the t + 1 iteration, X

best

the current optimal individual (food), α

and α

are weight

coeﬃcients that control the tendency of individuals to move

towards the optimal individual and the previous individual,

a is a constant used to determine the extent to which the tuna

follow the optimal individual and the previous individual in

the initial phase, t denotes the number of current iteration,

max

is the maximum iterations, and b is a random number

uniformly distributed between 0 and 1.

When all tuna forage spirally around the food, they have

good exploitation ability for the search space around the

food. However, when the optimal individual fails to ﬁnd

food, blindly following the optimal individual to forage is

not conducive to group foraging. erefore, we consider

generating a random coordinate in the search space as a

reference point for spiral search. is facilitates each indi-

vidual to search a wider space and makes TSO with global

exploration ability. e speciﬁc mathematical model is de-

scribed as follows:

t+1

�

· X

rand

+ β · X

rand

− X

􏼌

􏼐 􏼑

+ α

· X

, i � 1,

· X

rand

+ β · X

rand

− X

􏼌

􏼐 􏼑

+ α

· X

i− 1

, i � 2, 3, ..., NP,

⎧

⎪

⎨

⎪

⎩

(7)

where X

rand

is a randomly generated reference point in the

search space.

In particular, metaheuristic algorithms usually perform

extensive global exploration in the early stage and then

gradually transition to precise local exploitation. erefore,

TSO changes the reference points of spiral foraging from

random individuals to optimal individuals as the iteration

increases. In summary, the ﬁnal mathematical model of the

spiral foraging strategy is as follows:

t+1

�

· X

rand

+ β · X

rand

− X

􏼌

􏼐 􏼑

+ α

· X

, i � 1,

· X

rand

+ β · X

rand

− X

􏼌

􏼐 􏼑

+ α

· X

i− 1

, i � 2, 3, ..., NP,

, if rand <

max

· X

best

+ β · X

best

− X

􏼌

􏼐 􏼑

+ α

· X

, i � 1,

· X

best

+ β · X

best

− X

􏼌

􏼐 􏼑

+ α

· X

i− 1

, i � 2, 3, ..., NP,

, if rand ≥

max

⎧

⎪

⎨

⎪

⎩

(8)

2.2.3. Parabolic Foraging. In addition to feeding by forming

a spiral formation, tunas also form a parabolic cooperative

feeding. Tuna forms a parabolic formation with food as a

reference point. In addition, tuna hunt for food by searching

around themselves. ese two approaches are performed

simultaneously, with the assumption that the selection

probability is 50% for both. e speciﬁc mathematical model

is described as follows:

t+1

�

best

+ rand · X

best

− X

􏼐 􏼑

+ TF · p

· X

best

− X

􏼐 􏼑

, if rand <0.5,

TF · p

· X

, if rand ≥0.5,

⎧

⎪

⎨

⎪

⎩

(9)

p � 1 −

max

􏼠 􏼡

t/t

max

( )

(10)

where TF is a random number with a value of 1 or − 1.

Tuna hunt cooperatively through two foraging strategies

and then ﬁnd their prey. For the optimization process of TSO,

the population is ﬁrst randomly generated in the search space.

In each iteration, each individual randomly chooses one of the

two foraging strategies to execute, or chooses to regenerate the

position in the search space according to probability z. e

value of parameter z will be discussed in the parameter setting

simulation experiments. During the entire optimization

process, all individuals of TSO are continuously updated and

calculated until the end condition is met, and then the optimal

individual and the corresponding ﬁtness value are returned.

e TSO pseudocode is shown in Algorithm 1. e detailed

process of TSO is shown in Figure 1.

Computational Intelligence and Neuroscience 3

3. Numerical Experiment and Discussion

3.1. Benchmark Function Set and Compared Algorithms.

In this section, in order to evaluate the performance of the

TSO proposed in this paper, a set of well-known benchmark

functions are employed for testing. is set of benchmark

functions include 7 unimodal functions, 6 multimodal

functions, and 10 multimodal functions with ﬁxed dimen-

sions. e unimodal functions F1–F7 have only one global

optimal solution and are, therefore, often employed to

evaluate the local exploitation capability of an algorithm.

Besides the global optimal solution, the multimodal func-

tions F8–F23 also have multiple local optimal solutions and

are, therefore, used to challenge the global exploration ca-

pability and local optimal avoidance capability of an algo-

rithm. e mathematical formulas and characteristics of

these functions are shown in Table 1. A three-dimensional

visualization of these functions is given in Figure 2.

Return the best individual X

best

and the best ﬁtness value F (X

best

)

Start

Initialize the random

population of tunas

Assign free parameters

a and z

Calculate the ﬁtness

values of tunas

Update a

, a

, p

Rand<z

Yes

Update the position

using Eq. (1)

Rand<0.5

Update the position

using Eq. (9)

Yes

t/t

max

<rand

Yes

Update the position

using Eq. (7)

Update the position

using Eq. (2)

t<t

max

End

Yes

Figure 1: Flowchart of TSO.

Input: the population size NP and maximum iteration t

max

Output: the location of food (the best individual) and its ﬁtness value

Initialize the random population of tunas X

int

(i �1, 2, . . ., NP)

Assign free parameters a and z

While (t <t

max

)

Calculate the ﬁtness values of tunas

Update X

best

For (each tuna) do

Update α

, α

, p

If (rand <z) then

Update the position X

t+1

using equation (1)

Else if (rand ≥z) then

If (rand <0.5) then

If (t/t

max

<rand) then

Update the position X

t+1

using Equation (7)

Else if (t/t

max

≥rand) then

Update the position X

t+1

using Equation (2)

Else if (rand ≥0.5) then

Update the position X

t+1

using Equation (9)

End for

t � t + 1

End while

Return the best individual X

best

and the best ﬁtness value F(X

best

LGORITHM

Pseudocode of TSO.

4 Computational Intelligence and Neuroscience

Table 1: Description of benchmark functions.

Test function Name Type Dim Range Optimum

(x) � 􏽐

i�1

Sphere US 30 [− 100, 100] 0

(x) � 􏽐

i�1

| + 􏽑

i− 1

| Schwefel 2.22 UN 30 [− 10, 10] 0

(x) � 􏽐

i�1

(􏽐

j− 1

)

Schwefel 1.2 UN 30 [− 100, 100] 0

(x) � max

|, 1 ≤i ≤D􏼈 􏼉 Schwefel 2.21 US 30 [− 100, 100] 0

(x) � 􏽐

i�1

100(x

i+1

− x

)

+ (x

− 1)

Rosenbrock UN 30 [− 30, 30] 0

(x) � 􏽐

i�1

(

􏼄

+ 0.5

􏼅􏼁

Step US 30 [− 100, 100] 0

(x) � 􏽐

i�1

+ random[0, 1) Quartic US 30

[− 1.28,

1.28]

(x) � 􏽐

i�1

− x

sin(

��

􏽰

) Schwefel 2.26 MS 30 [− 500, 500] − 418.9829

∗

(x) � 􏽐

i�1

− 10 cos(2πx

) + 10 sin) Rastrigin MS 30

[− 5.12,

5.12]

(x) � 20 + e − 20 exp(− 20

��

(1/D)􏽐

i�1

􏽱

) − exp((1/D)􏽐

i�1

cos(2πx

)) Ackley MS 30 [− 32, 32] 8.8818e− 16

(x) � (1/4000)􏽐

i�1

) − (􏽑

i�1

cos(x

�

√

)) + 1 Griewank MN 30 [− 600, 600] 0

(x) � (π/D) 10sin

(πy

) + 􏽐

i�1

− 1)

[1 + 10sin

(πy

i+1

)] + (y

− 1)

􏽮 􏽯

+ 􏽐

i�1

u(x

, 10, 100, 4), y

� 1 + ((x

+ 1)/4)u(x

, a, , km) �

k(x

− a)

, x

0, − a <x

k(− x

− a)

, x

⎧⎪

⎨

⎪

⎩

Penalized MN 30 [− 50, 50] 0

(x) � 0, 1 sin

(3πx

) + 􏽐

i�1

− 1)

[1 + sin

(3πx

)] + (x

− 1)

[1 + sin

(2πx

)]

􏽮 􏽯

+ 􏽐

i− 1

u(x

, 5, 100, 4)(π/D) 10sin

(πy

􏼈 􏼉

+ 􏽐

i�1

u(x

, 10, 100, 4) Penalized2 MN 30 [− 50, 50] 0

(x) � ((1/500) + 􏽐

j�1

(1/(j + 􏽐

i�1

− a

)

)))

− 1

Foxholes MS 2

[− 65.53,

65.53]

0.998004

(x) � 􏽐

i�1

− (x

+ b

)/b

+ b

+ x

))

− 1

Kowalik MS 4 [− 5, 5] 0.0003075

(x) � (4x

− 2.1x

+ 1/3x

+ x

− 4x

+ x

)

Six hump

camel back

MN 2 [− 5, 5] − 1.03163

(x) � (x

− (5.1/4π

+ (5/π)x

− 6)

+ 10(1 − (1/8π)cos x

+ 10) Branin MS 2

[− 5, 10]×

[0, 15]

0.398

(x) � [1 + (x

+ x

+ 1)

(19 − 14x

+ 3x

− 14x

+ 6x

+ 3x

)] × [30 + (2x

− 3x

)

(18 − 32x

+ 12x

+ 48x

− 36x

+ 27x

)]

Goldstein

price

MN 2 [− 5, 5] 3

(x) � − 􏽐

i�1

exp(− 􏽐

j− 1

− p

))

) Hartman 3 MN 3 [0, 1] − 3.8628

(x) � − 􏽐

i�1

exp(− 􏽐

j− 1

− p

))

) Hartman 6 MN 6 [0, 1] − 3.32

(x) � − 􏽐

i�1

[(X − a

)(X − a

)

+ c

]

− 1

Langermann

MN 4 [0, 10] − 10.1532

(x) � − 􏽐

i�1

[(X − a

)(X − a

)

+ c

]

− 1

Langermann

MN 4 [0, 10] − 10.4029

(x) � − 􏽐

i�1

[(X − a

)(X − a

)

+ c

]

− 1

Langermann

MN 4 [0, 10] − 10.5364

Computational Intelligence and Neuroscience 5

评论收藏

内容反馈

版权申诉

德善934

2022-06-27

用户下载后在一定时间内未进行评价，系统默认好评。
Teacher曾

2023-01-21

资源不错，内容挺好的，有一定的使用价值，值得借鉴，感谢分享。
刘永锐

2023-01-15

资源内容详尽，对我有使用价值，谢谢资源主的分享。
映月辉

2022-02-01

用户下载后在一定时间内未进行评价，系统默认好评。
weixin_38716205

2022-01-29

用户下载后在一定时间内未进行评价，系统默认好评。

前往

页

临风听雨~

粉丝: 36
资源: 96

智能优化算法：金枪鱼群优化算法tuna swarm optimization algorithm

最新资源

智能优化算法：金枪鱼群优化算法tuna swarm optimization algorithm

Matlab实现基于TSO-XGBoost金枪鱼算法优化XGBoost的多输入单输出数据回归预测（完整源码和数据）

基于金枪鱼算法求解单目标优化问题（tso Tuna swarm optimization，TSA）.zip

2014年最新提出的仿生群智能优化算法 Chicken swarm Optimization Algorithm

【优化求解】基于金枪鱼算法求解目标matlab代码.zip

捕食者算法

TugaSUSE:金枪鱼-开源

粒子群优化算法Particle swarm optimization algorithm

非洲秃鹫优化算法（African vultures optimization algorithm, AVOA)源代码

Archimedes_optimization_algorithm_a_new_metaheuris阿基米德优化算法

Brown bear optimization algorithm 棕熊优化算法 Matlab

【故障识别】基于金枪鱼优化算法TSO优化门控单元GRU实现故障诊断附Matlab代码.rar

人工智能算法集

基于混合策略改进的樽海鞘群智能优化算法+基于混合策略改进的群智能优化算法在支持向量机回归（SVR）中的应用，Matlab代码

repo1.22-20160724

windows下python 3.9 Numpy scipy和matlabplot的安装教程详解

hbase-2.4.16-bin.tar.gz

anaconde-conda安装清华源.pdf

oh-my-tuna:保持冷静并使用 TUNA 镜子

PSO算法IGPSOexe.zip_PSO_PSO algorithm_pso算法_swarm-optimization_模式识

优化觅食算法 Optimal foraging algorithm for global optimization（OFA）

白骨顶鸡优化算法COOT_optimization_algorithm

matlab代码粒子群算法-Particle-swarm-optimization:粒子群优化

anaconda安装及环境配置教程

解决pip install psycopg2出错问题

PIP和conda 更换国内安装源的方法步骤

阿里云服务器linux系统搭建Tomcat部署Web项目

Eclipse jee最新版 国内镜像较快的

最新资源

Eclipse jee最新版国内镜像较快的