
DSP 课程设计报告
设计题目: 256 点 FFT
院 系: 计算机科学学院
专 业: 自动化
年 级: 2008 级
姓 名:
学 号:
指导教师:
2011 年 11 月 28 日

中南民族大学计算机科学学院 08 级自动化专业 宗子轩 08064056 第 1 页 共 22 页
256 点 FFT 的实现
一、设计目的
1、 加深对 DFT 算法原理和基本性质的理解;
2、 熟悉 FFT 的算法原理和 FFT 子程序的算法流程和应用;
3、 学习用 FFT 对连续信号和时域信号进行频谱分析的方法;
4、 学习 DSP 中 FFT 的设计和编程思想;
5、 学习使用 CCS 的波形观察器观察波形和频谱情况;
二、设计内容
给定 256 采样点,求频谱,统计运行时间并在 PC 上显示。
三、设计原理
快速傅里叶变换(FFT)是一种高效实现离散傅里叶变换(DFT)的快速算法,是数字信
号处理中最为重要的工具之一,它在声学,语音,电信和信号处理等领域有着广泛的应用。
快速傅里叶变换 FFT
旋转因子 WN 有如下的特性。
对称性: WNk+N/2=-WNk
周期性:WNn(N-k)=WNk(N-n)=WN-nk
利用这些特性,既可以使 DFT 中有些项合并,减少了乘法积项,又可以将长序列的 DFT
分解成几个短序列的 DFT。FFT 就是利用了旋转因子的对称性和周期性来减少运算量的。
FFT 的算法是将长序列的 DFT 分解成短序列的 DFT。例如:N 为偶数时,先将 N 点的 DFT
分解为两个 N/2 点的 DFT,使复数乘法减少一半:再将每个 N/2 点的 DFT 分解成 N/4 点的 DFT,
使复数乘又减少一半,继续进行分解可以大大减少计算量。最小变换的点数称为基数,对于
基数为 2 的 FFT 算法,它的最小变换是 2 点 DFT。
一般而言,FFT 算法分为按时间抽取的 FFT(DIT FFT)和按频率抽取的FFT(DIF
FFT)两大类。DIF FFT 算法是在时域内将每一级输入序列依次按奇/偶分成2个短序列进
行计算。而 DIF FFT 算法是在频域内将每一级输入序列依次奇/偶分成2个短序列进行计算。
两者的区别是旋转因子出现的位置不同,得算法是一样的。在 DIF FFT 算法中,旋转因子出
现在输入端,而在 DIF FFT 算法中它出现在输入端。
假定序列 x(n)的点数 N 是 2 的幂,按照 DIF FFT 算法可将其分为偶序列和奇序列。
偶序列:x(2r)=x1(r)

中南民族大学计算机科学学院 08 级自动化专业 宗子轩 08064056 第 2 页 共 22 页
奇序列:x(2r+1)=x2(r)
其中:r=0,1,2,…,N/2-1 则 x(n)的 DFT 表示为
式中,x1(k)和 x2(k)分别为 x1(r)和 x2(r)的 N/2 的 DFT。
由于对称性,
WNk+N/2=-WNk。因此,N 点 DFT 可分为两部分:
前半部分:x(k)=x1(k)+WkNx2(k) (4)
后半部分: x(N/2+k)=x1(k)-WkNx2(k) k=0,1,…,N/2-1 (5)
从式(4)和式(5)可以看出,只要求出 0~N/2-1 区间 x1(k)和 x2(k)的值,就可求出 0~N-1
区间 x(k)的 N 点值。
以同样的方式进行抽取,可以求得 N/4 点的 DFT,重复抽取过程,就可以使 N 点的 DFT
用上组 2 点的 DFT 来计算,这样就可以大减少运算量。
基 2 DIF FFT 的蝶形运算如图(a)所示。设蝶形输入为 X1(K)和 X2((K),输出为 x(k)和
x(N/2+K),则有
x(k)=x1(k)+WkNx2(k) (6)
x(N/2+k)=x1(k)-WkNx2(k) (7)
在基数为 2 的 FFT 中,设 N=2M,共有 M 级运算,每级有 N/2 个 2 点 FFT 蝶形运算,因
( ) ( ) ( ) ( )
1 1 1
0 0 0
N N N
nk nk nk
N N N
n n n
X k x n W x n W x n W
- - -
= = =
= = +
å å å
n为偶数
n为奇数
( ) ( )
( )
/2 1 /2 1
2 1
2
0 0
2 2 1
N N
r k
rk
N N
r r
x r W x r W
- -
+
= =
= + +
å å
( )
( )
( )
( )
/2 1 /2 1
2 2
1 2
0 0
N N
rk rk
k
N N N
r r
x r W W x r W
- -
= =
= +
å å
( ) ( )
/2 1 /2 1
1 /2 2 /2
0 0
N N
rk k rk
N N N
r r
x r W W x r W
- -
= =
= +
å å
( ) ( )
1 2
k
N
X k W X k= +
, 0,1,... / 2 1r k N= -
中南民族大学计算机科学学院 08 级自动化专业 宗子轩 08064056 第 3 页 共 22 页
此,N 点 FFT 总共有 MN/2 个蝶形运算。
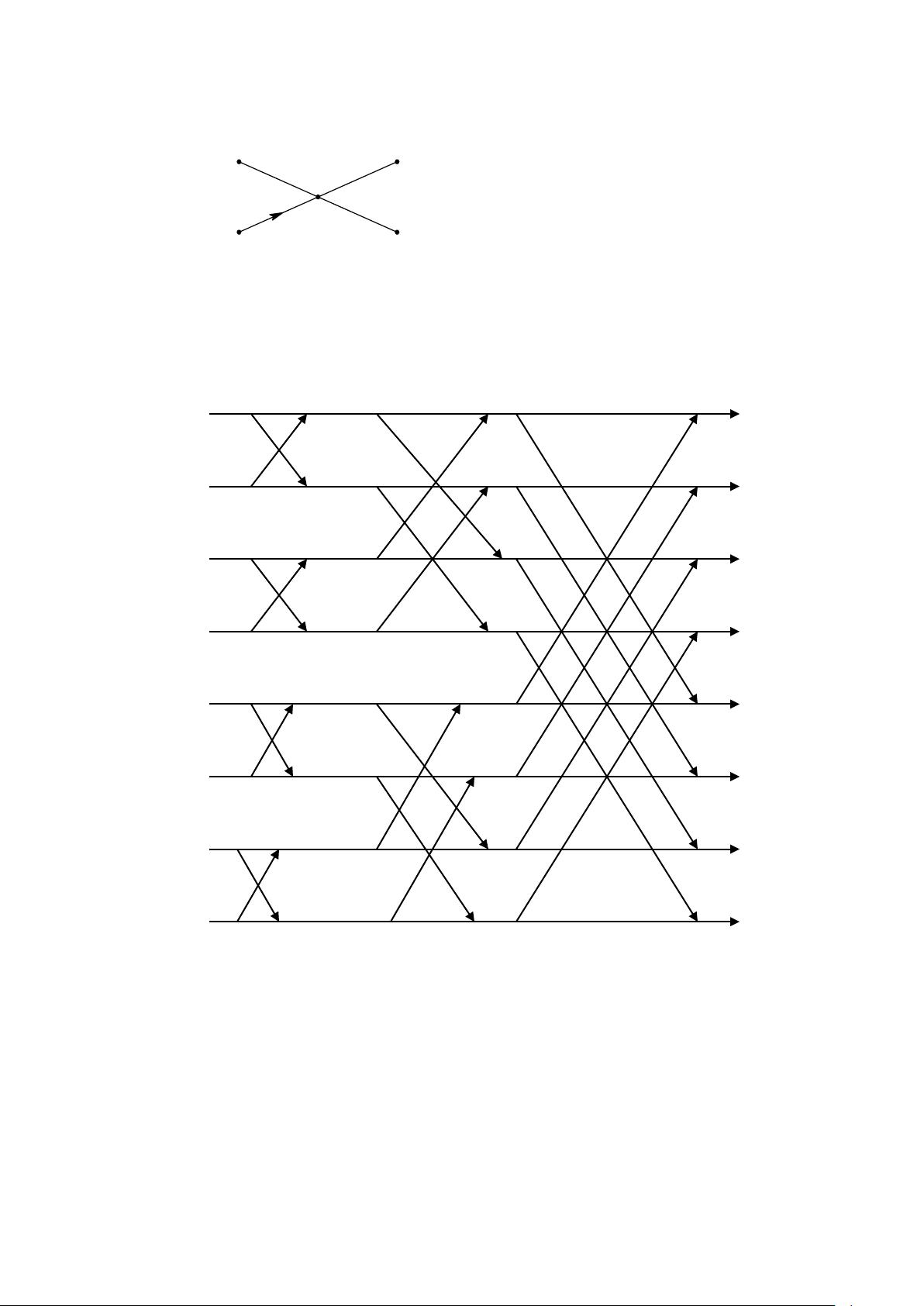
图(a) 基 2 DIF FFT 的蝶形运算
例如:基数为 2 的 FFT,当 N=8 时,共需要 3 级,12 个基 2 DIT FFT 的蝶形运算。其信
号流程如图(b)所示。
x(0) x(0)
W
N
0
x(4) x(1)
-1
W
N
0
x(2) x(2)
-1
W
N
0
W
N
2
x(6) x(3)
-1
-1
W
N
0
x(1) x(4)
-1
W
N
0
W
N
1
x(5) x(5)
-1 -1
W
N
0
W
N
2
x(3) x(6)
-1 -1
W
N
0
W
N
2
W
N
3
x(7) x(7)
-1 -1 -1
图(b) 8 点基 2 DIF FFT 蝶形运算
从图(b)可以看出,输入是经过比特反转的倒位序列,称为位码倒置,其排列顺序为
x(0),x(4),x(2),x(6),x(1),x(5),x(3),x(7) , 输 出 是 按 自 然 顺 序 排 列 , 其 顺 序 为
x(0),x(1),x(2),x(3),x(4),x(5),x(6),x(7)。
C
A
B
A
£«
BC
A
£
BC
中南民族大学计算机科学学院 08 级自动化专业 宗子轩 08064056 第 4 页 共 22 页
四、设计步骤
1、 启动 CSS。
2、 加载工程项目。















评论0