1
现代数字信号处理仿真报告
3.16 计算机模拟实验。
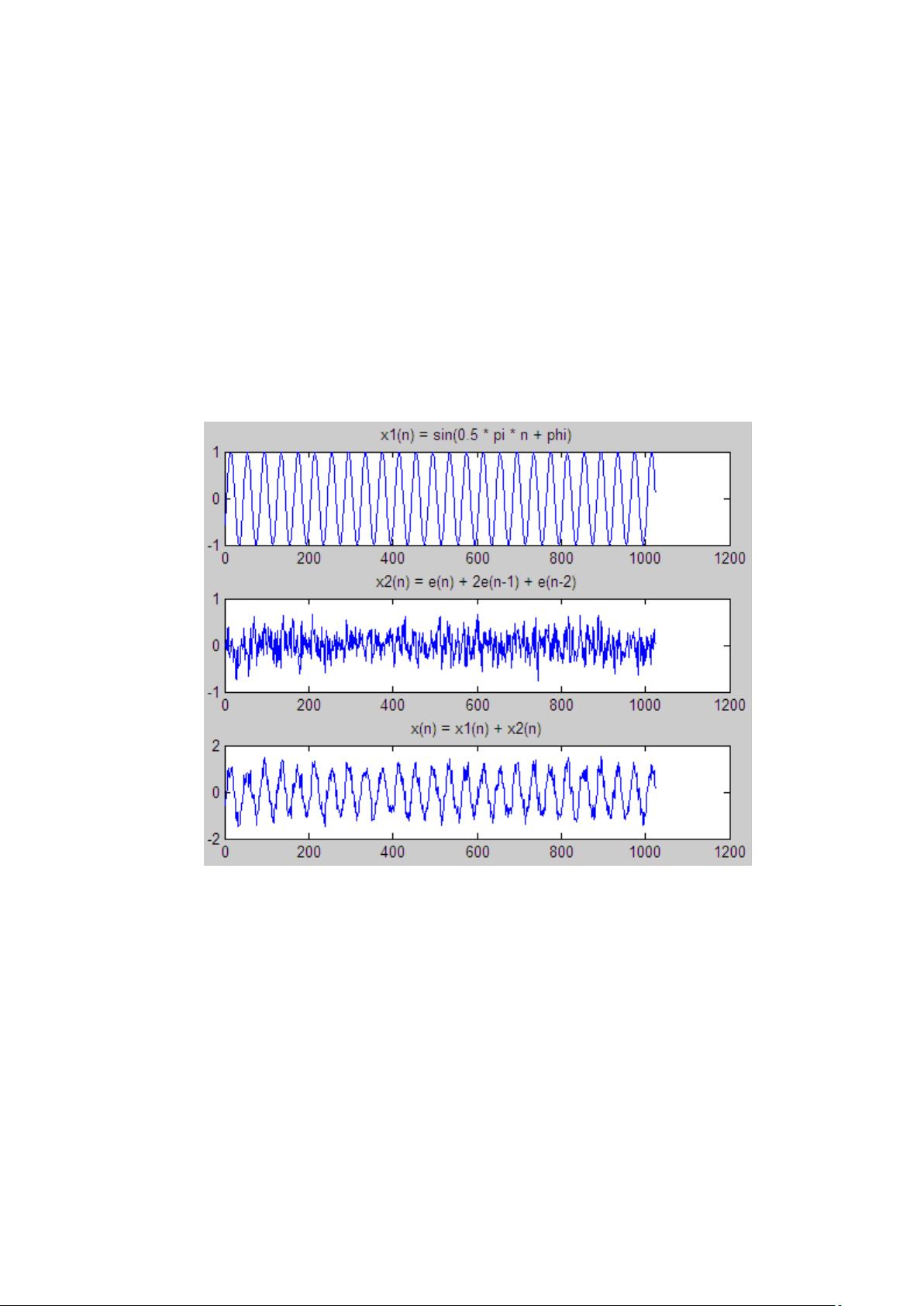
设 x(n) = x
1
(n) + x
2
(n),x
1
(n)是窄带信号,定义为 x
1
(n) = sin(0.05πn +φ),φ是在[0, 2
π)区间上均匀分布的随机相位。x
2
(n)是宽带信号,它由一个零均值、方差为 1 的白噪声信
号 e(n)激励一个线性滤波器而产生,其差分方程为 x
2
(n) = e(n) + 2e(n-1) + e(n-2)。
(1)计算 x
1
(n)和 x
2
(n)各自的自相关函数,并画出其函数图形。据此选择合适的延时,以
实现谱线增强。
(2)产生一个 x(n)序列。选择合适的μ值。让 x(n)通过谱线增强器。画出输出信号 y(n)和
误差信号 e(n)的波形,并分别与 x
1
(n)和 x
2
(n)进行比较。
解:
一.仿真思路:
首先,根据题目要求生成各个信号,包括窄带信号 x
1
(n)、白噪声 e(n)、宽带噪声信号 x
2
(n)
以及输入信号 x(n)。然后,根据生成的信号,分别计算 x
1
(n)和 x
2
(n)的自相关函数。其次,
观察前述两个自相关数的图形,找出二者的自相关长度,并选择一个介于两自相关长度值之
间的一个值,作为Δ值,将输入信号 x(n)延迟Δ,即 x(n-Δ)。最后,按照课本上图 3.45 所
示的自适应预测原理完成自适应滤波,其中,自适应滤波器采用 LMS 算法,算法内容见课
本 3.7 节。
二.数学原理
1.自适应的最小均方(LMS)算法
LMS 算法的核心思想是用平方误差代替均方误差,并用这个平方误差来近似二次性能
曲面的梯度。这样可以推导出 LMS 算法的权系数基本关系式
w
(n+1) =
w
(n) -
μ▽
(n) =
w
(n) + 2
μe
(n)
x
(n)
滤波器每输入一个数据 x(n),按照当前权系数
w
(n)滤波输出数据 y(n)后,再根据期望信
号 d(n)和输出信号 y(n)计算出相应的误差
e
(n),接着按照权系数更新关系式更新权矢量
w
(n+1)。下一时刻,再利用新的权矢量
w
(n+1)对数据进行滤波。如果
μ
值选取的合适,那
么经过一定的更新步数后,系统的权矢量
w
将会收敛到一个固定的
w
*
附近,也就是,这个
时候,自适应滤波器已达到了稳定滤波阶段。
2.自适应预测
若将自适应干扰抵消器中的输入信号用有用信号的时延来取代,则构成自适应预测器,
其原理如图 3.45 所示。当完成自适应调整后,将自适应滤波器的参数复制到预测滤波器上,
那么后者的输出便是对有用信号的预测,预测时间与试验时间相等。
自适预测可以用来分离窄带信号和宽带信号。如果输入信号时以一个窄带信号 s
N
(n)和
一个宽带信号 s
B
(n)的混合,窄带信号的自相关函数 R
N
(k)比宽带信号的自相关函数 R
B
(k)的
有效宽度要短。当延迟时间选为 k
B
< Δ < k
N
时,信号 s
B
(n)与 s
B
(n-Δ)将不再相关,而 s
N
(n)
与 s
N
(n-Δ)仍然相关,因而自适应滤波器输出的将只是 s
N
(n)的最佳估计 s
N
(n),s
B
(n) + s
N
(n)
与 s
N
(n)相减后将得到 s
B
(n)的最佳估计 s
B
(n),这样就把 s
N
(n)和 s
B
(n)分开了。