Principle of Communication System 3.2.pptx-综合文档
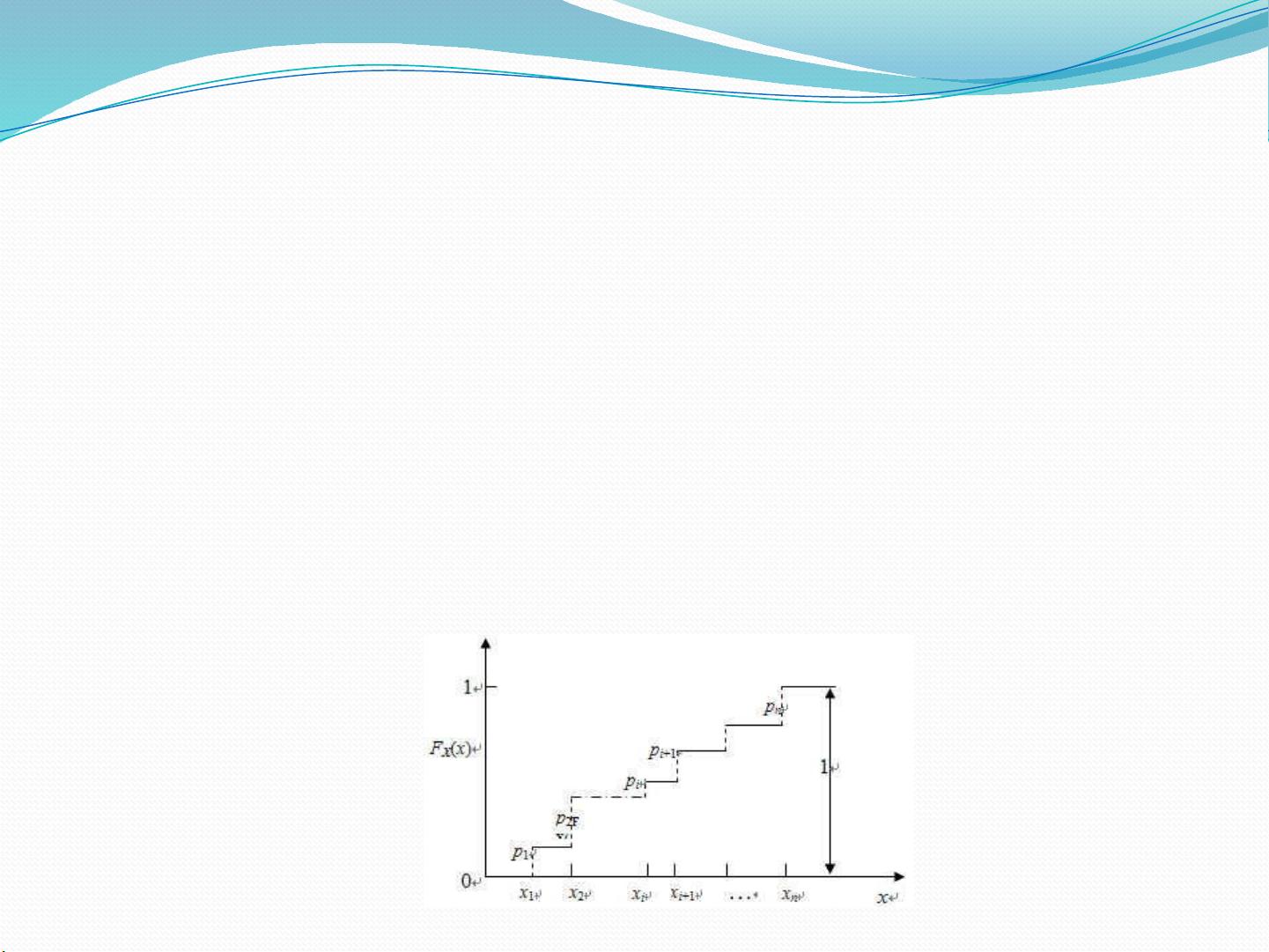
《通信系统原理3.2》课程讲解主要涵盖了随机变量的概率分布及其特性,这对于理解通信系统中的信号处理至关重要。以下是对这些知识点的详细阐述: 1. 随机变量的概率分布: - 对于离散随机变量,其可能的取值为 ${x_1} \leq {x_2} \leq \cdots \leq {x_i} \leq \cdots \leq {x_n}$,相应的概率分别为 ${p_1}, {p_2}, \ldots, {p_n}$。离散随机变量的概率分布函数 ${F_X}(x)$ 定义为:${P(X < x_1)} = 0$,${P(X \leq x_n)} = 1$。且 ${F_X}(x)$ 是单调递增函数,${F_X}(-\infty) = 0$,${F_X}(\infty) = 1$。 2. 随机变量的概率密度: - 对于连续随机变量,概率密度函数 ${f_X}(x)$ 定义为:${P(a < X \leq b)} = \int_a^b f_X(x) dx$,其累积分布函数 ${F_X}(x)$ 是一个连续的单调递增函数,且 $\int_{-\infty}^{\infty} f_X(x) dx = 1$,同时 $f_X(x) \geq 0$。 - 对于离散随机变量,其分布函数 ${F_X}(x)$ 为 ${F_X}(x) = \sum_{i=1}^{n} p_i u(x - x_i)$,其中 $u(x)$ 是单位阶跃函数。离散随机变量的概率密度可以通过分布函数得到,即 $f_X(x) = \sum_{i=1}^{n} p_i \delta(x - x_i)$,其中 $\delta(x)$ 是Dirac delta函数。 3. 常见的概率分布举例: - 正态分布:概率密度函数 ${f_X}(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$,其中 $\mu$ 是均值,$\sigma$ 是标准差。其概率密度曲线呈钟形,中心对称于均值 $\mu$。 - 均匀分布:概率密度函数 ${f_X}(x) = \frac{1}{b-a}$,对于 $a \leq x \leq b$,其他区间为0。其概率密度曲线在 $(a, b)$ 区间内是水平的,表示所有在这段区间的取值概率相等。 - 瑞利分布:主要用于描述无线通信中的衰落现象,概率密度函数涉及更复杂的数学表达式,通常在无线电工程中出现。 以上内容是通信系统理论的基础,对于分析和建模通信系统的噪声、干扰以及信号传输质量等至关重要。了解这些概率分布特性,有助于我们更好地理解和设计通信系统中的信号处理算法,以提高通信的可靠性和效率。



剩余17页未读,继续阅读
- 粉丝: 5
- 资源: 970
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0