没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

西 北 师 范 大 学 学 报 (自然科学版) 第 45 卷 2009 年第 5 期
Journal of Northwest Normal University (Natural Science) Vol畅45 2009 No畅5
收稿日期 : 2008桘12桘12 ;修改稿收到日期 :2009桘05桘20
基金项目 : 国家自然科学基金资助项目(60671063 ;10871122)
作者简介 : 高霞 (1979 — ) ,女 ,甘肃天水人 ,讲师 ,硕士研究生 .主要研究方向为生态数学 .
E桘mail :
g
aoxia1012@
y
ahoo畅cn
具 有 时 滞 和 干 扰 的 广 义 Logistic 模 型 的
Hopf 分 支 周 期 解
高 霞
1 ,2
,陈斯养
1
(1畅 陕西师范大学 数学与信息科学学院 ,陕西 西安 710062 ;
2畅 甘肃工业职业技术学院 基础学科部 ,甘肃 天水 741025)
摘 要 :讨论了具有时滞与干扰的广义 Logistic 模型分支周期解的存在性 、 稳定性及其近似分支周期解 . 首先根据特
征值理论得到该模型产生 Hopf 分支的条件 ; 然后用周期函数正交性方法得到其近似分支周期解的表达式 ; 最后举例
验证了定理的可实现性 , 利用 Matlab 得到了其参数取不同数值时的曲线拟合图 , 并讨论了参数对周期解的周期和振
幅的影响 .
关键词 : Logistic 模型 ;周期解 ; Hopf 分支 ;时滞 ;稳定性
中图分类号 : O 175畅7 文献标识码 : A 文章编号 :1001‐988 Ⅹ (2009)05‐0006‐07
T he Hopf bifurcation periodic solution of a general Logistic model
with time delay and interference
GAO Xia
1 ,2
, CHEN Si桘
y
ang
1
(1畅 College of Mathematics and Information Science ,Shaanxi Normal University ,Xi摧an 710062 , Shaanxi ,China ;
2畅 Department of Basic Courses , Gansu Industrial Vocational Technical College , Tianshui 741025 ,Gansu , China)
Abstract : The existence , stability and approximate expression of Hopf bifurcation periodic solution are
discussed for a class of general Logistic model with time delay and interference . First of all , the condition
of forming bifurcation periodic solution is obtained according to the eigenvalue theory . After that , the
form of approximate periodic solution is derived by the orthogonal method . In the end , the achievability
of the results is verified by examples . The fitted curves are achieved by Matlab w hen assign the different
p
armaters to the model , and the effect of parameters on the amplitude of vibration and the period of the
p
eriodic solution for the model is analysed .
Key words : Logistic model ;
p
eriodic solution ; Hopf bifurcation ; time delay ; stability
1 模型的引入
种群的持续生存和灭绝是种群动力学研究的一个重要问题 ,而时滞对种群能否持续生存有着重要的影
响
[1桘9]
, 因此研究时滞产生 Hopf 分支周期解问题具有重要的实际意义 . 文献[ 4 ]研究了非线性系统
d x(t)
dt
+
ax (t) + bx (t
-
τ
) =
f
(x(t) ,x(t
-
τ
))
的分支周期解问题 ; 文献[ 1 ]研究了一类具有固定收获率 , 且含有时滞与干扰的模型
6
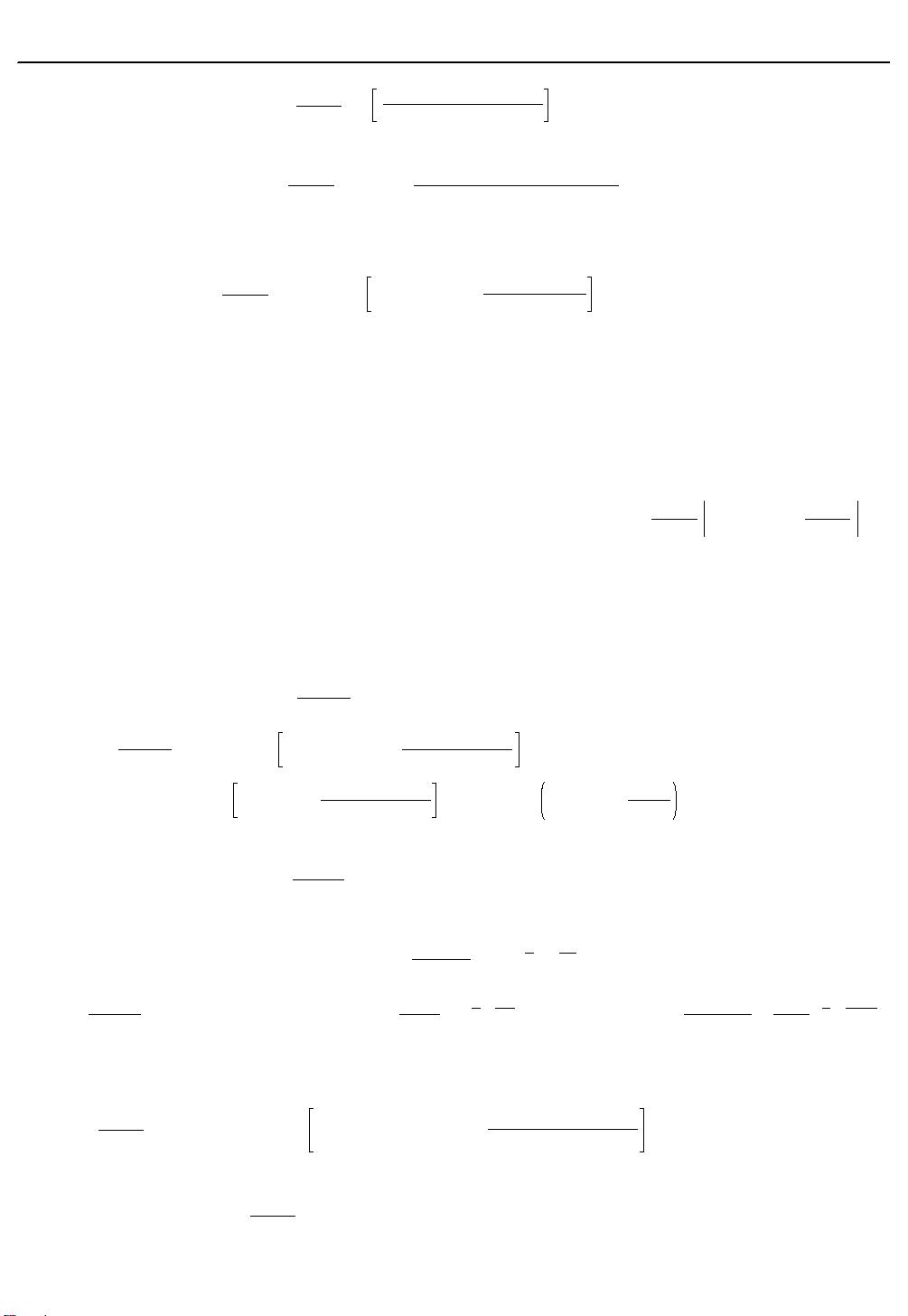
2009 年第 5 期 高霞等 : 具有时滞和干扰的广义 Logistic 模型的 Hopf 分支周期解
2009 No畅5 The Hopf bifurcation periodic solution of a general Logistic model with time delay and interference
dx(t)
dt
=
K
-
rx (t)x
n
(t
-
τ
)
1
+
cx
n
(t
-
τ
)
θ
-
H ;
文献[ 8 ]讨论了模型
dx(t)
dt
=
rx (t)
1
-
c
1
x
α
(t) - c
2
x
β
(t
-
τ
)
1
+
c
3
x
β
(t
-
τ
)
的分支周期解问题 , 并给出了近似分支周期解的表达式 . 本文研究了一类具有放养率 ,且含时滞和扰动参
数
α
,
β
的广义 Logistic 模型
d x(t)
dt
=
x(t
-
τ
)
a
-
b x (t) -
c x (t)
d
+
x(t
-
τ
)
α
+
h x
β
(t) ( 1 )
的 Hopf 分支周期解问题 . 其中 a ,b ,c ,d ,h ,
τ
均为正常数 ;
α
,
β
是外界对种群密度的干扰因子 , 且
α
,
β
∈
(0 ,+ ∞ ) . 初始条件为
x(
θ
) =
φ
(
θ
) ≥ 0 ,
θ
∈
[-
τ
,0] ,
φ
(
θ
) ∈ C([-
τ
,0] ,R
+
) ,
φ
(0) > 0 . ( 2 )
2 平衡态的稳定性和局部 Hopf 分支的存在性
引理 1 模型( 1 )满足初始条件( 2 )的解都是正的 .
证明 假设存在 t
1
> 0 ,使得在[0 ,t
1
)上有 x(t) > 0 , 而 x(t
1
) = 0 , 则有
dx(t)
dt
t = t
1
≤ 0 , 而
dx(t)
dt
t = t
1
= ax(t -
τ
) > 0 , 矛盾 .故不存在使得 x(t)= 0 的 t ,又因 x(t)关于 t 连续可微 , 所以 , x(t) > 0 在其定义
域上恒成立 ,引理得证 . 】
引理 2 模型( 1 )满足初始条件( 2 )的解是全局存在的 .
证明 假设模型( 1 )的解不是全局存在的 , 则存在 t
1
> 0 ,使得 lim
t → t
1
-
x(t) = + ∞ , 设 x(t)在 t
2
处第一
次到达任意点
δ
,即 x(t
2
)=
δ
, 则
dx(t
2
)
dt
≥ 0 ,而
d x(t
2
)
dt
=
x(t
2
-
τ
)
a
-
b x (t
2
) -
c x (t
2
)
d
+
x(t
2
-
τ
)
α
+
h x
β
(t
2
) =
x(t
2
-
τ
)
a
-
b
δ
-
c
δ
d
+
x(t
2
-
τ
)
α
+
h
δ
β
<
δ
a
-
b
δ
-
c
δ
d
+
δ
α
+
h
δ
β
=
0 ,
这与假设矛盾 , 所以模型( 1 )的解 x(t)是全局存在的 . 】
定理 1 若 0 <
β
≤ 1 ,且
α
=
2m + 1
2n+ 1
(m ,n ∈ N) , 则系统( 1 )有唯一的正平衡态存在 .
证明 由模型( 1 )可知 ,其正平衡态 x
倡
应满足
a
-
b x
倡
-
c x
倡
d
+
x
倡
= -
h
1
α
x
倡
β
-
1
α
,
其中
α
=
2m + 1
2n + 1
(m ,n ∈ N) . 令 F(x)= a - bx -
cx
d + x
+ h
1
α
x
β
- 1
α
, 则 F
′
(x) = - b -
cd
(d + x)
2
+
β
- 1
α
h
1
α
x
β
-
α
- 1
α
.
若 0 <
β
≤ 1 , 此时 F(0) = a> 0 且 F(x)单调递减 ,故方程( 1 )的平衡态存在且唯一 . 】
做变换 x(t) =
y
(t) + x
倡
,则模型( 1 )变为
d
y
(t)
dt
=
[
y
(t
-
τ
) + x
倡
]
a
-
b(
y
(t) + x
倡
) -
c(
y
(t) + x
倡
)
d
+
y
(t
-
τ
) + x
倡
α
+
h[
y
(t) + x
倡
]
β
. ( 3 )
将( 3 )式右边在
y
= 0 处 Taylor 展开得
d
y
(t)
dt
+
A
y
(t) + B
y
(t
-
τ
) = F(
y
(t) ,
y
(t
-
τ
)) , ( 4 )
其中
F(
y
(t) ,
y
(t
-
τ
)) = A
20
y
2
(t) + A
11
y
(t)
y
(t
-
τ
) + A
02
y
2
(t
-
τ
) + A
30
y
3
(t) + A
21
y
2
(t)
y
(t
-
τ
) +
7
剩余6页未读,继续阅读
资源评论

weixin_38660359
- 粉丝: 3
- 资源: 961
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 激光摆动焊接abaqus温度场分析 圆形 正弦摆动 同金属 异种金属摆动焊接温度场分析 基于高斯热源 双椭球热源 柱热源 模型和子程序文件
- TPU-MLIR算法量化及YOLOv5s模型转换与优化实践
- EXE格式应用程序11
- API加解密签名算法-实验代码
- onnx量化裁减调优TPU-MLIR使用
- 盼盼短剧系统整合版.pptx
- 基于FPGA的HDMI显示控制器+项目源码+文档说明
- iXhash2-4.00.tar.gz SpamAssassin 的非官方改进版 iXhash 插件
- 机械设计鱼缸玻璃贴膜sw21可编辑非常好的设计图纸100%好用.zip
- IT8导入云程序,联网,双击打开指定目录即可
- iXhash2-2.05.tar.gz iXhash2 是 SpamAssassin 的非官方改进版 iXhash 插件
- 机械设计永磁转子清洁机sw21非常好的设计图纸100%好用.zip
- 色彩 IT8 Delta E差值大数据计算,配合上传文件使用,下载中查找
- 毕业设计答辩模板PPT
- iC65N 2P 用于EPLAN部件EDZ,包含图片、STP、窗口宏ema、部件库EDZ
- VS2022 C++ gRPC demo 程序
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功