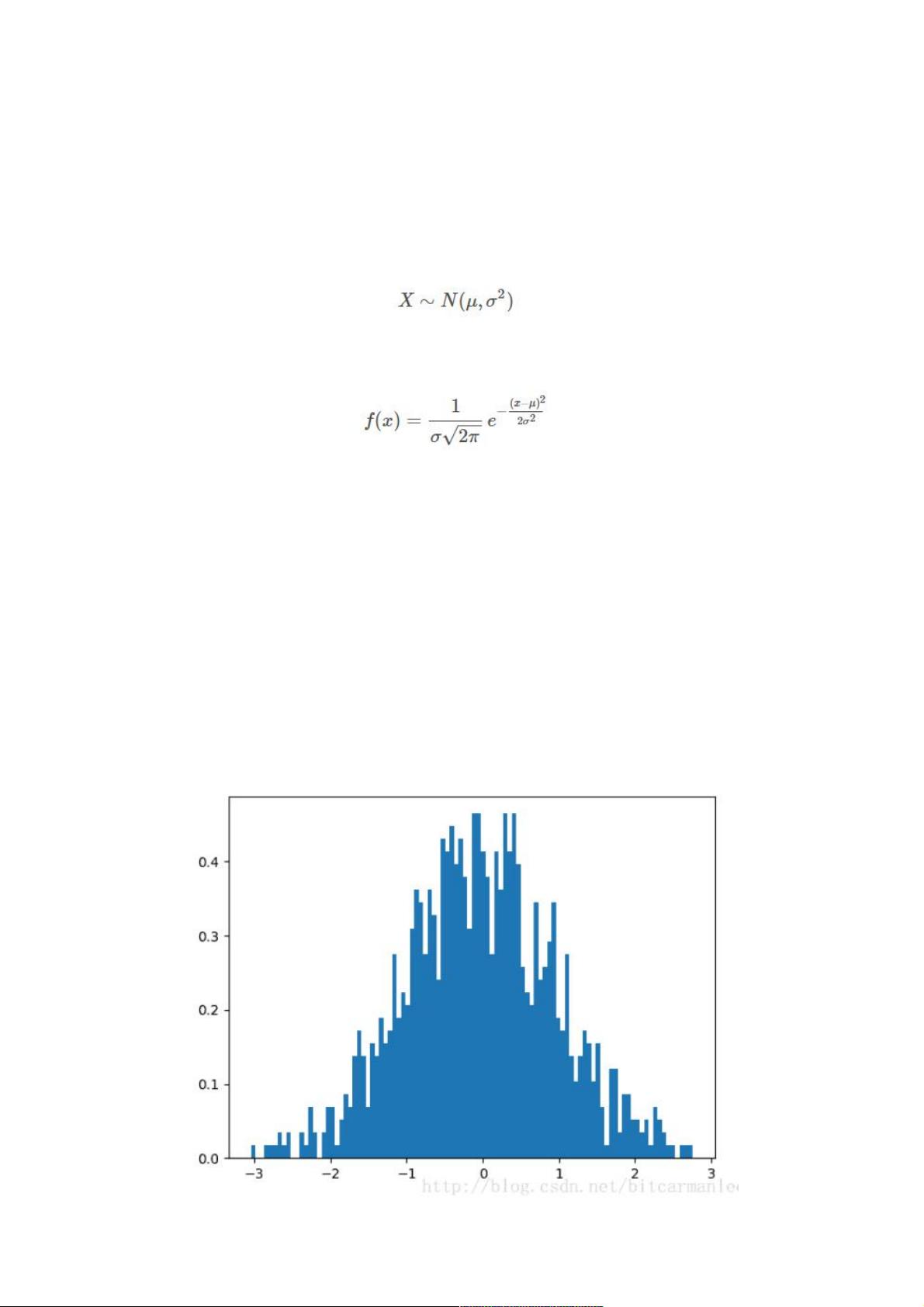
在Python编程环境中,绘制正态分布图像是一种常见且实用的统计可视化方法,尤其在数据分析和机器学习领域。正态分布,又称高斯分布,是概率论中的一种重要分布,广泛存在于自然界和社会科学的各种现象中。它由两个参数定义:位置参数μ(均值)和尺度参数σ(标准差),其概率密度函数形式为: \[ f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] 正态分布的图形特征是一个对称的钟形曲线,其中均值μ决定了曲线的中心位置,标准差σ则影响了曲线的宽度。当μ=0, σ=1时,该分布称为标准正态分布。 在Python中,我们可以利用numpy、matplotlib库来绘制正态分布的图像。以下是一些关键步骤: 1. 导入必要的库: ```python import numpy as np import matplotlib.mlab as mlab import matplotlib.pyplot as plt ``` 2. 生成正态分布的随机数据: 使用`np.random.normal()`函数,输入均值μ、标准差σ以及样本数量sampleNo,生成对应正态分布的随机数序列。 ```python mu, sigma = 0, 1 sampleNo = 1000 s = np.random.normal(mu, sigma, sampleNo) ``` 3. 绘制直方图: 使用`plt.hist()`函数,传入生成的随机数序列,设置直方图的柱子数量(bins),以及是否按概率密度进行归一化(normed=True)。 ```python plt.hist(s, bins=100, normed=True) ``` 4. 显示图像: 使用`plt.show()`展示直方图。 ```python plt.show() ``` 如文中所述,生成的直方图可能并不完全符合理想的正态分布形状,这通常是因为样本数量不够大。随着样本数量的增加(例如增大sampleNo),直方图会更接近正态分布的理论形态。 为了使图像更具解释性,我们还可以添加正态分布的概率密度曲线。`mlab.normpdf()`函数用于计算正态分布的概率密度值,将其与直方图一起绘制,可以直观地对比实际数据与理论分布的吻合程度。以下是如何实现这一功能的示例: ```python def demo2(): mu, sigma, num_bins = 0, 1, 50 x = mu + sigma * np.random.randn(1000000) n, bins, patches = plt.hist(x, num_bins, normed=True, facecolor='blue', alpha=0.5) y = mlab.normpdf(bins, mu, sigma) plt.plot(bins, y, 'r--') plt.xlabel('期望值') plt.ylabel('概率') plt.title('正态分布的直方图: $\mu = 0$, $\sigma=1$') plt.subplots_adjust(left=0.15) plt.show() ``` 在这个例子中,我们不仅绘制了直方图,还用红色虚线展示了对应的正态分布曲线。通过这种方式,我们可以更好地理解和验证数据是否遵循正态分布。 Python提供了强大的工具来绘制正态分布图像,这对于理解数据分布特性、进行假设检验和参数估计等统计分析任务至关重要。通过调整样本数量和绘制曲线,我们可以直观地评估数据集是否符合正态分布,并进行相应的分析。

- 粉丝: 6
- 资源: 916
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- springboot项目酒店管理系统.zip
- springboot项目旧物置换网站.zip
- springboot项目家具销售电商平台.zip
- springboot项目简历系统.zip
- springboot项目交流互动系统().zip
- MATLAB代码:含电热联合系统的微电网运行优化火 关键词:微网 电热联合系统 优化调度 综合能源系统 仿真平台:MATLAB yalmip+cplex 主要内容:提出基于电热联合调度的区域并
- phpenc加密程序源码
- springboot项目家具网站.zip
- springboot项目汉服推广网站.zip
- springboot项目火车订票管理系统.zip
- 用PHP完整的网站开发视频教程最新版本
- springboot项目二手交易平台.zip
- springboot项目点餐平台网站.zip
- springboot项目滴答拍摄影项目.zip
- springboot项目大学生社团活动平台.zip
- 1553b 源码 代码 支持所有 模式 asic FPGA


 信息提交成功
信息提交成功