没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论
、、
199
'6年第
36
卷
清华大学学报〈自然科学版〉
Journal
of
Tsinghua
University
(Sci
&.
Tech)
11/19
第
3
期第
59-64
页
应变空间表述的混凝土弹塑性搞合本构模型
张承拉j1
J
信卢
清华大学工程力学系,北京
100084
文
摘考虑到岩土类材料的应变软化和弹塑性桐合特点,从Il
'yushin
公设出发,把弹性模量
看成是塑性应变的函数,直接从应变空间构造初始屈服函数并确定加载函数,推导出一个应变
空间表述的本构模型。该模型不但可以描述材料的强化段,而且可以描述材料的软化段并能反
映材料弹塑性精合的性质.给出的两个简单算例说明了该模型的有效性.
关键词混凝土
F
应变空间
z
弹塑性精合
F
本构关系
分羹号
033.346
近
20
年来,混凝土全曲线实验增多,人们将注意力集中在如何描述这类材料软化段的本
构关系上。由于经典塑性理论基于
Drucker
公设,不能应用于软化材料,人们开始以应变为基
本自变量,以Jl
'yushin
公设为基础,提出了应变空间表述的本构理论。从Il
'y
归
ushin
导出的塑性理论不但适用于材料的强化段,而且适用于材料的软化段,表达形式统一。
因结构计算的需要,出现了许多应变空间表述的本构模型。但是,由于实验数据相对缺乏,
离散性很大,至今仍没有被广泛承认的本构模型。在以往提出的本构模型中,大多没有考虑弹
塑性榈合的问题。而弹塑性桐合是岩土类介质的突出特点之一。殷有泉等[1]对弹塑性藕舍问题
在理论上进行了推导,对广义正交法则进行了讨论。
Han
和
Chen[2]
将Do
ugill
的断裂模型推
广,提出了较有影响的塑性断裂模型。
本文从Jl
'yushin
公设出发,推导出一个较为简单的本构模型。直接从应变空间中确定屈
服函数和加载函数。最后给出两个简单的算例。
1
基本假设及定义
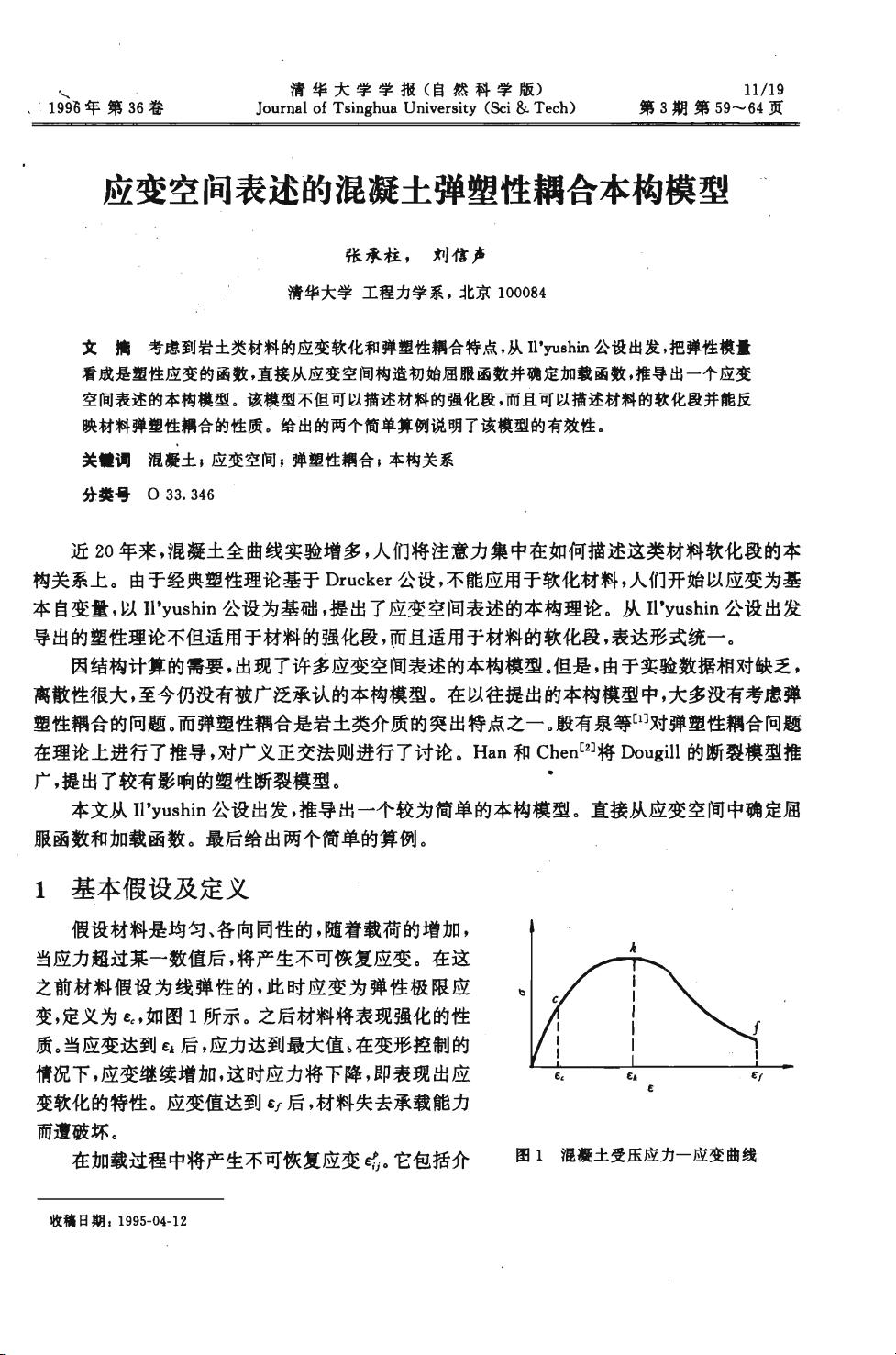
假设材料是均匀、各向同性的,随着载荷的增加,
当应力起过某一数值后,将产生不可恢复应变。在这
之前材料假设为线弹性的,此时应变为弹性极限应
变,定义为
Ec'
如图
1
所示。之后材料将表现强化的性
质。当应变达到马后,应力达到最大值
b
在变形控制的
情况下,应变继续增加,这时应力将下降,即表现出应
变软化的特性。应变值达到
εf
后,材料失去承载能力
而遭破坏。
在加载过程中将产生不可恢复应变
4
。它包括介
收稿日期
I
1995-04-12
k
b
图
1
混凝土受压应力一应变曲线
资源评论

weixin_38618540
- 粉丝: 3
- 资源: 943
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 【岗位说明】办事处经理岗位职责.doc
- 【岗位说明】办事处经理职能说明书.doc
- 【岗位说明】仓库管理员岗位职责说明书.doc
- 【岗位说明】采购专员岗位职责.doc
- 【岗位说明】厂长岗位职责.doc
- 【岗位说明】财务助理岗位职责.doc
- 【岗位说明】采购经理岗位职责.doc
- 【岗位说明】大区经理岗位职责.doc
- 【岗位说明】大区经理的职能描述书.doc
- 【岗位说明】车间主任岗位职责.doc
- 【岗位说明】服务业各部门职能描述.doc
- 【岗位说明】副总经理岗位职责.doc
- 【岗位说明】副厂长职务描述书.doc
- 【岗位说明】副厂长岗位职责.doc
- 【岗位说明】副总经理职务描述书.doc
- 【岗位说明】工厂人事经理岗位说明书.doc
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功