Variable-curvaturemicroresonatorsfordual-wavelengthlasing资源-CSDN文库

31 浏览量 2021-02-04 05:22:26 上传评论收藏 2.01MB PDF 举报

资源推荐

资源详情

资源评论

Variable-curvature microresonators for

dual-wavelength lasing

MIN TANG,YONG-ZHEN HUANG,* YUE-DE YANG,HAI-ZHONG WENG, AND ZHI-XIONG XIAO

State Key Laboratory on Integrated Optoelectronics, Institute of Semiconductors, University of Chinese Academy of Sciences, Chinese Academy

of Sciences, Beijing 100083, China

*Corresponding author: yzhuang@semi.ac.cn

Received 25 July 2017; revised 7 October 2017; accepted 17 October 2017; posted 18 October 2017 (Doc. ID 303255); published 13 November 2017

Stable dual-mode semiconductor lasers can be applied for the photonic generation of microwave and terahertz

waves. In this paper, the mode characteristics of a variable curvature microresonator are investigated by a two-

dimensional finite element method for realizing stable dual-mode lasing. The microresonator features a

smooth boundary and the same symmetry as a square resonator. A small variable-curvature microresonator with

a radius of 4 μm can support the fundamental four-bounce mode and the circular-like mode simultaneously, with

quality factors up to the order of 10

and 10

, respectively. The dual modes in the phase space of the Poincaré

surface of sections distribute far from each other and can maintain enough stability for dual-mode lasing.

Furthermore, the refractive index and waveguide can modulate the dual-mode wavelength difference and quality

factors efficiently thanks to the spatially separated fields of these two modes.

OCIS codes: (140.3948) Microcavity devices; (140.5960) Semiconductor lasers.

https://doi.org/10.1364/PRJ.5.000695

1. INTRODUCTION

Whispering-gallery mode (WGM) microcavities, which con-

fine light by total internal reflection with the advantages of high

quality (Q) factors and small mode volumes, have attracted

great attention in the research of fundamental physics and

optoelectronics applications [1]. Circular microresonators in

different geometries were successfully used in the demonstra-

tion of ultralow-threshold microlasers, but the rotational sym -

metry causes a significant difficulty to efficiently collect the

emission light from the microlasers. Deformed microresonators

such as spiral [2], limaçon [3], quadrupole [4], flattened quad-

rupole [5], and ellipse-shaped [6] have been proposed to break

rotational symmetry for realizing directional emission. By di-

rectly connecting an output waveguide to the microresonators,

directional emission could also be realized [7–9]. Recently,

circular-side polygonal microresonators were also proposed and

demonstrated for Q factor control and mode selection [10,11].

Besides the directional emission and Q factor control, dual-

wavelength laser sources that could be used for microwave or

terahertz generation have also attracted great attention. There

are several ways of producing dual lasing sources, such as

Fabry–Perot (FP) cavities integrated by Y junction [12], dual-

section vertical-cavity surface-emitting lasers [13,14], dual-

section distributed feedback (DFB) lasers [15], fiber lasers

based on fiber Bragg gratings [16,17], and square microcavity

lasers [10,18]. In this paper, we propose and numerically in-

vestigate a deformed optical variable curvature microresonator

(VCM) with a mixture shape of microsquare and microdisk

resonators for stable dual-mode lasing. This VCM can support

two types of high Q factor modes, the four-bounce mode and

the circular-like mode. By carefully modifying perimeter distri-

bution and waveguide position, stable dual-mode lasing with

directional emission can be achieved according to the numerical

simulation results.

This paper is organized as follows. In Section 2, the mode

characteristics of the VCM are simulated based on two-

dimensional (2D) finite element method (FEM). A ray dynam-

ics analysis is also performed for the high Q factor modes. In

Section 3, dual-mode stability is analyzed for the VCM and

circular and square microresonators theoretically. The modula-

tion of the mode wavelengths and quality factors, based on

graphic electrode and waveguide positions, are investigated nu-

merically. Finally, the summary is given in Section 4.

2. MODE CHARACTERISTICS

The schematic diagram of a 2D VCM is given in Fig. 1. There

are four zero-curvature points distributed in the midpoints of

square edge, and the connecting arcs between these points have

a linear variable curvature. The curvature of the arc in the first

quadrant can be expressed as

θ



rdθ 0 < θ ≤

rdθ

< θ ≤

; (1)

Research Article

Vol. 5, No. 6 / December 2017 / Photonics Research 695

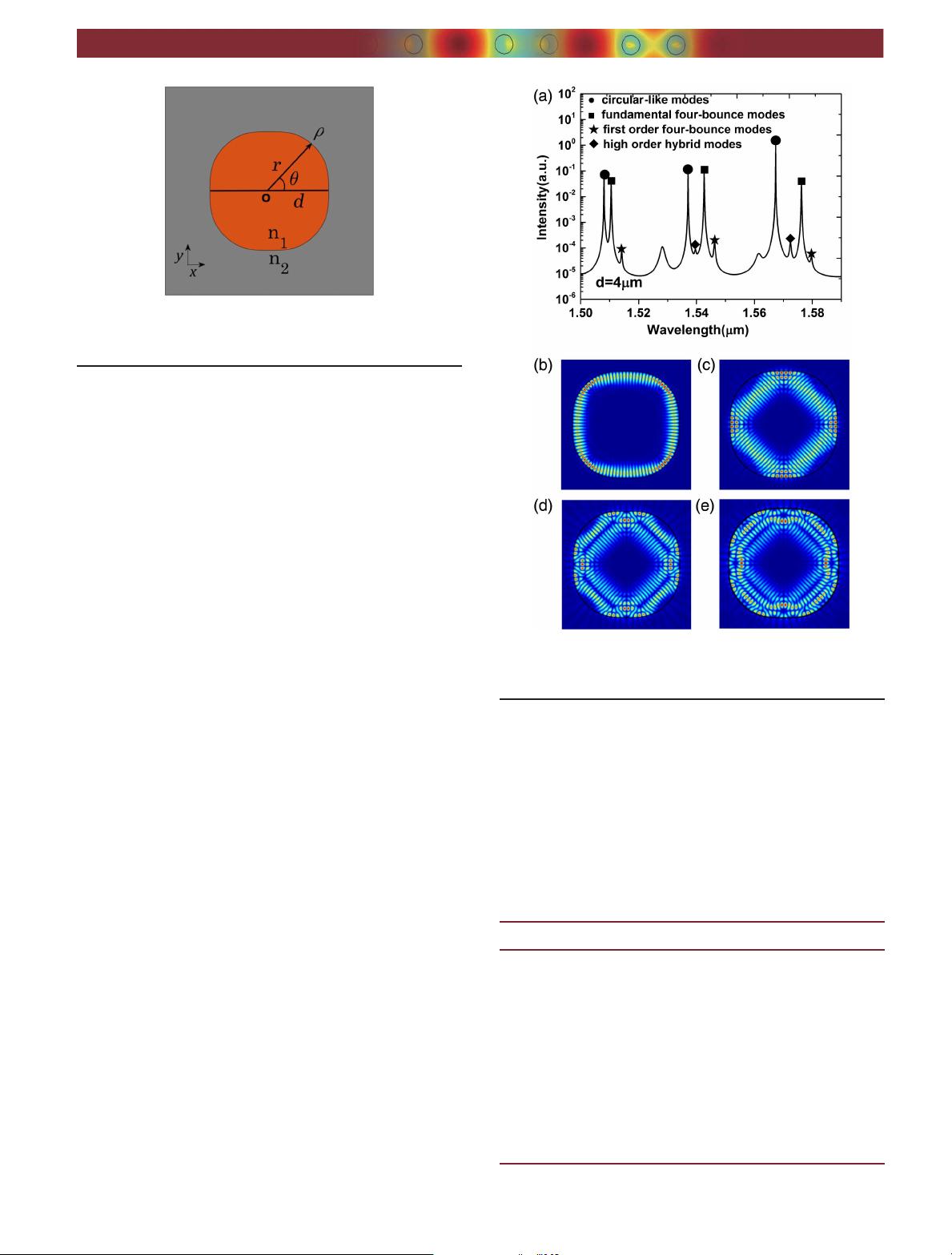
where ρ, r, and θ are the curvature, polar radius, and angle,

respectively, and k is a parameter showing the changing speed

of curvature along the boundary. The microresonator size is

determined by the parameter d, which is half the distance be-

tween the two opposite zero-cur vature points. The curvature in

the other quadrants is a periodic function as ρθ − π∕2ρθ.

The VCM in different sizes could be proved similar to each

other with the product of maximum curvature ρ

max

and VCM

size d equaling 19.82. The deformation degree ε is defined as

ε r

max

− r

min

∕r

min

, which is a fixed number of 0.065 for

the VCM. With a continuous variation of the curvature along

the boundary, the boundary is smooth and second-order differ-

entiable, leading to the emergence of the circular-like mode de-

spite large deformation compared with the circular resonator.

The same symmetry properties between the VCM and

microsquare resonators also herald the same periodic orbits

of optical rays.

The mode characteristics of the VCM are simulated by 2D

FEM (COMSOL Multiphysics 5.0). The refractive indices of

the resonator and outside media are set to 3.2 and 1.54, respec-

tively, for the InP-based VCM and surrounded bisbenzo

cyclobutene. The microresonator size is 4 μm. A perfect

matched layer absorbing boundary with a width of 0.5 μm

is used to terminate the simulation area. The intensity spectrum

for TE modes with a wavelength resolution of 0.08 nm is

obtained and plotted in Fig. 2(a). The spectrum shows that

there are three sets of longitudinal modes, ranging from

1.50 to 1.59 μm. The four kinds of high-Q modes marked

by circles, squares, five-pointed stars, and prisms represent

the circular-like mode, fundamental four-bounce mode,

first-order four-bounce mode, and high-order hybrid mode,

respectively, with the field distributions of jH

j as presented

in Figs. 2(b)–2(e). The circular-like modes have relatively

higher Q factors up to 4.34 × 10

with the field distributing

mostly along the boundary, similar to the WGMs in a circular

microresonator. The reflection positions of the four-bounce

modes concentrate on four zero-curvature points with reflec-

tion angles of around 45°. The photons of the four-bounce

modes are more likely to reach leaky regions, leading to

lower-mode Q factors in the order of 10

. The longitudinal

mode intervals around 1.55 μm are 29 and 33 nm for

the circular-like modes and the fundamental four-bounce

modes, respectively. The first-order four-bounce modes and

high-order hybrid modes have mode Q factors in the order

of 10

. The details of mode wavelengths and Q factors are

summarized in Table 1.

The VCM could be regarded as a mixture of circular and

square shapes. For the comparison between these three types

Fig. 1. Schematic diagram of a 2D VCM. The curvature is linearly

changed as the boundary starting from zero curvature points to the

neighboring maximum-curvature points.

Fig. 2. (a) Mode intensity spectrum and mode field patterns jH

j of

the (b) circular-like mode, (c) fundamental four-bounce mode,

(d) first-order four-bounce mode, and (e) high-order hybrid mode.

Table 1. Wavelengths and Q Factors for Symmetric TE

Modes in VCM with d  4 μm

Mode Wavelength (μm) Q Factor

Circular-like modes 1.5072 4.34 × 10

1.5372 1.68 × 10

1.5664 4.51 × 10

Four-bounce modes 1.5096 1.51 × 10

1.5428 1.51 × 10

1.5753 1.25 × 10

First-order four-bounce modes 1.5133 4.13 × 10

1.5453 3.27 × 10

1.5787 2.81 × 10

High-order hybrid modes 1.5083 2.42 × 10

1.5397 2.61 × 10

1.5726 2.76 × 10

696 Vol. 5, No. 6 / December 2017 / Photonics Research

Research Article

剩余6页未读，继续阅读

评论收藏

内容反馈

weixin_38607026

粉丝: 9
资源: 914

Variable-curvature microresonators for dual-wavelength lasing

Exploring Curvature

PCL-Principal-Curvature-CAN-master.zip

PyPI 官网下载 | one-relator-curvature-0.0.9.tar.gz

Gauss-curvature and mean-curvature.rar

matlab开发-curvature

论文研究-Curvature Computing Based on Shape Operator for Implicit Surfaces.pdf

calc-curvature:用于计算曲率的ios应用程序，使用cordova

matlab2016b代码-CURE-Curvature-Regularization-Via-Biharmonic-Extension:“C

High efficiency X-ray diffraction diagnostic spectrometer with multi-curvature bent crystal

用卷积滤波器matlab代码-Curvature-Model:曲率模型

matlab计算曲面的曲率代码-Global-Surface-Curvature-Mean:此函数通过在每个顶点上制作点并计算这些点相对于其相

Hypersurfaces with Prescribed $lpha$-Relative Gauss-Kronecker Curvature

An Efficient Exact-PGA Algorithm for Constant Curvature Manifolds

Max-Curvature:Max Curvurature算法在手指静脉特征提取中的实现

Remarks on sub-supersolution methods for prescribed mean curvature equations

An Improved Streamline Curvature Approach for Off-Design Analysis

Slow axis collimation lens with variable curvature radius for semiconductor laser bars

Python库 | one_relator_curvature-0.1.2-py3-none-any.whl

论文研究-基于深度信息的指尖追踪及手势识别.pdf

curvature_curvature_matlab_曲率_曲率计算_

路径规划论文 --英文

Corner.rar_NOISE_contour_following_curvature-scale_edge extract_

Model Predictive Stabilization Control of High-speed Autonomous Ground Vehicles

curvature_curvature_点云曲率_C++_pointcloud_

Riemannian Manifolds-An Introduction to Curvature(GTM176).pdf

mean curvature

Spacelike hypersurfaces with constant $r$-th mean curvature in the anti-de Sitter spaces

基于偏微分的图像去噪图像恢复CDD,曲率驱动扩散方法（CDD）是三阶PDEmatlab.zip

最新资源