一组机器人的决策和有限时间运动控制资源-CSDN文库

37 浏览量 2021-03-10 22:02:37 上传评论收藏 1.42MB PDF 举报

资源推荐

资源详情

资源评论

738 IEEE TRANSACTIONS ON CYBERNETICS, VOL. 43, NO. 2, APRIL 2013

Decision Making and Finite-Time Motion

Control for a Group of Robots

Qiang Lu, Member, IEEE, Shirong Liu, Xiaogao Xie, Member, IEEE, and Jian Wang

Abstract—This paper deals with the problem of odor source

localization by designing and analyzing a decision–control system

(DCS) for a group of robots. In the decision level, concentration

magnitude information and wind information detected by robots

are used to predict a probable position of the odor source. Speciﬁ-

cally, the idea of particle swarm optimization is introduced to give

a probable position of the odor source in terms of concentration

magnitude information. Moreover, an observation model of the

position of the odor source is built according to wind information,

and a Kalman ﬁlter is used to estimate the position of the odor

source, which is combined with the position obtained by using

concentration magnitude information in order to make a decision

on the position of the odor source. In the control level, two types

of the ﬁnite-time motion control algorithms are designed; one is

a ﬁnite-time parallel motion control algorithm, while the other

is a ﬁnite-time circular motion control algorithm. Precisely, a

nonlinear ﬁnite-time consensus algorithm is ﬁrst proposed, and a

Lyapunov approach is used to analyze the ﬁnite-time convergence

of the proposed consensus algorithm. Then, on the basis of the

proposed ﬁnite-time consensus algorithm, a ﬁnite-time parallel

motion control algorithm, which can control the group of robots

to trace the plume and move toward the probable position of

odor source, is derived. Next, a ﬁnite-time circular motion control

algorithm, which can enable the robot group to circle the probable

position of the odor source in order to search for odor clues,

is also developed. Finally, the performance capabilities of the

proposed DCS are illustrated through the problem of odor source

localization.

Index Terms—Decision theory, intelligent control, multirobot

systems, robot motion.

I. INTRODUCTION

DOR source localization, which is a type of ill-posed

and dynamical optimization problem, has received much

attention from researchers and engineers due to its practical

signiﬁcance for human security, e.g., searching for the sources

of wastes and locating victims. In the l ast two decades, how to

Manuscript received March 24, 2012; revised June 20, 2012; accepted

August 11, 2012. Date of publication September 28, 2012; date of current

version April 16, 2013. This work was supported in part by the National Natural

Science Foundation of China under Grants 61175093, 60675043, and 51007015

and in part by the Natural Science Foundation of Zhejiang Province under Grant

Y1090426. This paper was recommended by Associate Editor S. X. Yang.

Q. Lu is with the College of Automation, Hangzhou Dianzi University,

Hangzhou 310018, China, and also with the Centre for Intelligent and

Networked Systems and the School of Information and Communication

Technology, Central Queensland University, Rockhampton, Qld. 4702,

Australia (e-mail: lvqiang@hdu.edu.cn).

S. Liu, X. Xie, and J. Wang are with the College of Automation, Hangzhou

Dianzi University, Hangzhou 310018, China (e-mail: liushirong@hdu.edu.cn;

xiexg@hdu.edu.cn; wangjian@hdu.edu.cn).

Color versions of one or more of the ﬁgures in this paper are available online

at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/TSMCB.2012.2215318

locate an odor source based on a single robot has been widely

studied. Three typical approaches, namely, chemotaxis [23],

[30], anemotaxis [8], [10], [13], [27], and infotaxis [32], have

been proposed. For chemotaxis where the local concentration

information is used, the robot is guided to move along the

gradient direction of concentration [23], [30]. For anemotaxis

where the local wind information is used, the main idea is to

use the local wind direction and detection events about odor to

orient the robot to locate the source of odor [8], [10], [13], [27].

For infotaxis where information gain instead of concentration

gradient is used, the reader is referred to [32] and the references

therein.

Recently, particle swarm optimization (PSO) [16], which

can make effective use of swarm information and individual

information to guide a particle swarm to search for the optimum

[28], has been used to coordinate a group of robots to deal with

the problem of odor source localization [15], [17], [21], [24]. To

avoid trapping into local maximal concentrations, for instance,

Jatmiko et al. [15] improved the commonly used PSO algorithm

based on an electrical charge theory charged particle swarm

optimization (CPSO). In the i mproved algorithm, two types of

robots (neutral and charged robots) are used. Among neutral

robots, there is no repulsive force, while among charged robots,

the mutual repulsive force is generated in order to maintain

the positional diversity of robots. To conveniently use the PSO

algorithm for odor source localization, Lu and Han [17] pro-

posed a distributed coordination control architecture where the

PSO algorithm is divided into three parts (prediction, plan, and

control). Accordingly, the cooperative control system consists

of three levels: a group level, a trajectory level, and a robot

level. In the group level, swarm information and individual

information are used to predict the probable position of the

odor source. In the trajectory level, a movement trajectory of

the robot is planned from the current position to the probable

position of the odor source. In the robot level, a control law

is designed to enable the robot to move along the planned

trajectory. This control architecture makes the control system

robust and evolvable [14]. In terms of this control architecture,

the s earch performance of the robot group coordinated by the

CPSO algorithm [15] is improved. To quickly l ocate t he odor

source, Lu and Han [21] proposed a probability PSO with

information-sharing mechanism. Due to introducing the ideas

of distribution estimation algorithm and niche, each robot can

be provided an opportunity to choose an appropriate position

in the search space such that the search performance of the

robot group can be improved. To sum up, one can conclude

from aforementioned research results in [15], [17], [21], and

[24] that the PSO algorithm provides a mechanism to predict

LU et al.: DECISION MAKING AND FINITE-TIME MOTION CONTROL FOR GROUP OF ROBOTS 739

a probable position of the odor source through swarm and

individual concentration information and then to adjust the

movement direction of robots to move toward the probable

position of the odor source.

However, it is worth mentioning that odor source localiza-

tion is a type of ill-posed problem (the global concentration

maximum is surrounded by multiple concentration maxima),

which may result in the local convergence of multiple robots

controlled by PSO algorithms. Moreover, odor source localiza-

tion is also a type of dynamical optimization problem, which

may result in no odor clues in the detection region of the

robot group. For the ﬁrst issue, in addition to concentration

information, wind information should also be used to predict

the probable position of the odor source since it is a main

factor to shape the plume containing odor clues. For the second

issue, the parallel motion of the robot group can be utilized

to extend the detection region, and the circular motion of

the robot group can be employed to search for odor clues.

Moreover, due to several advantages of ﬁnite-time controllers

such as higher control accuracy, better disturbance rejection,

and robustness against uncertainties [2]–[4], the ﬁnite-time

parallel and circular controllers can be designed to realize

the parallel motion and circular motion of the robot group,

respectively. Therefore, in order to develop a decision-control

system (DCS), it is of practical signiﬁcance to introduce wind

information into the decision level and to design a ﬁnite-time

parallel motion controller as well as a ﬁnite-time circular mo-

tion controller in the control level, which is the motivation of the

current study.

Flocking is a kind of collective behaviors, i.e., a large number

of individuals, such as birds, interact with each other for a

common group objective. Both the parallel motion and the

circular motion can be regarded as a class of ﬂocking behaviors

[7], [25], [26], [31]. However, for the problem of odor source

localization, we will use several robots, such as three to nine

robots, to deal with this problem. The results obtained in this

paper can be extended to a large group of robots. The idea

in this paper is in part from the work on the design of ﬁnite-

time controllers [5], [6], [33] and from the study of swarming

behaviors [11], [25]. A partial version of this paper appears in

[18] and [19]. Hence, in order to develop the DCS, we will ﬁrst

propose a distributed coordination control architecture, which

consists of two levels: a decision level and a control level.

Then, we will predict a probable position of the odor source

by employing concentration magnitude information and wind

information detected by the robot group in the decision level.

Next, we will derive a ﬁnite-time consensus algorithm and use

a Lyapunov approach to analyze the ﬁnite-time convergence of

the proposed consensus algorithm. In addition, on the basis of

the ﬁnite-time consensus algorithm, we will design a parallel

motion control algorithm in the control level, which can control

the robot group to trace the plume and move toward the prob-

able position of the odor source. Moreover, we will develop a

circular motion control algorithm in the control level, which

can control the robot group to circle the probable position of

the odor source in order to search for odor clues. Finally, we

will illustrate the performance capabilities of the proposed DCS

through the problem of odor source localization.

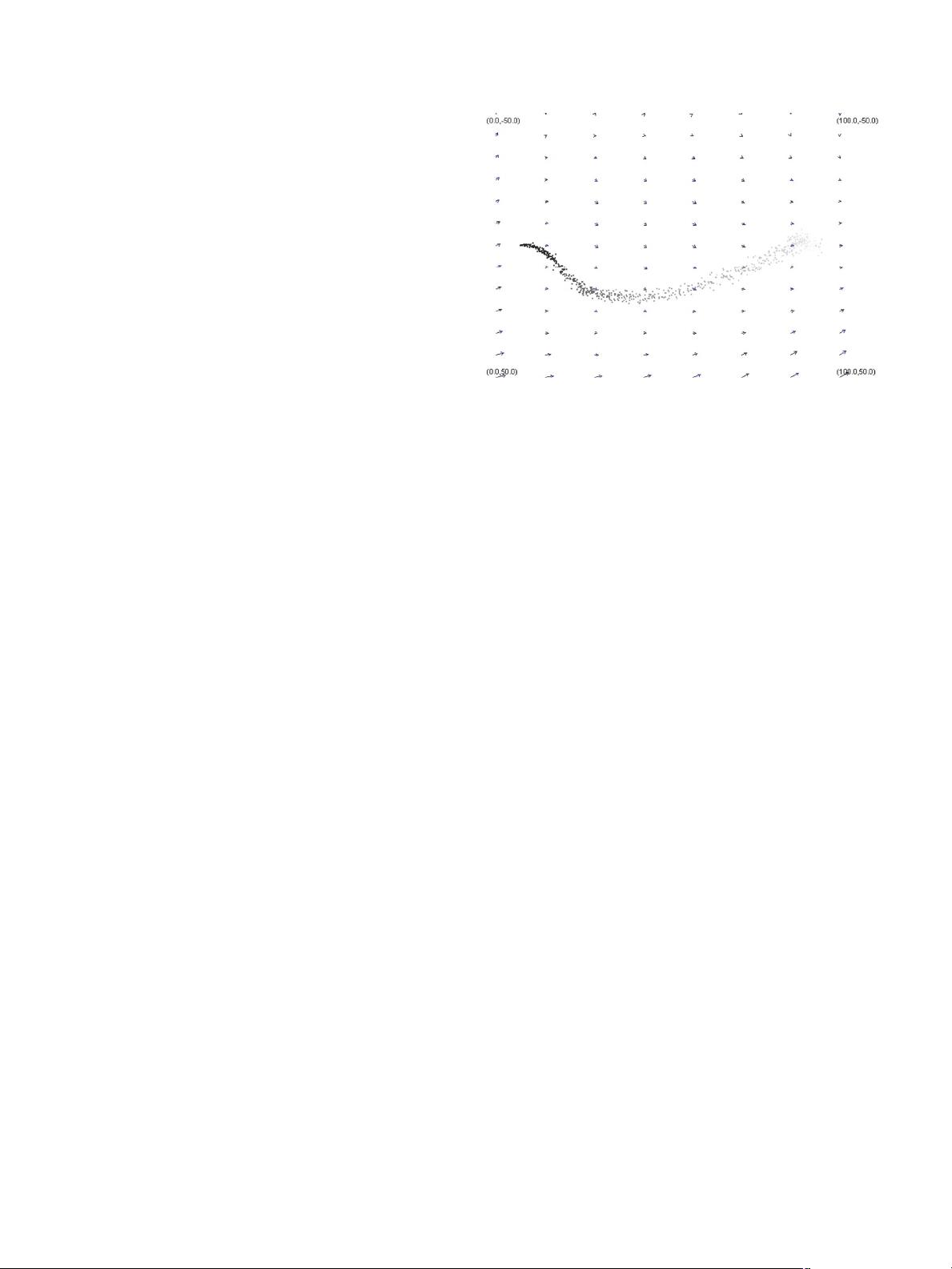
Fig. 1. Instantaneous plume where black dots denote the ﬁlaments that form

a plume and arrows denote the wind speed and direction.

Notation: l

denotes the index set {1, 2,...,N}.Let

sig(r)

=sign(r)|r|

, where 0 <α<1, r ∈ R, and sign(·) is

a sign function.

II. P

ROBLEM STATEMENT AND PRELIMINARIES

In this section, we will illustrate the problem of odor source

localization and introduce several preliminaries.

A. Odor Source Localization

Odor source localization is a type of ill-posed and dynamical

optimization problem, which can be stated as follows.

Problem 1: An odor source localization problem consists of

the following:

1) a set N of N mobile robots or vehicles;

2) a set X of positions in a 2-D search space R

;

3) a set M⊆N×Xof possible pairs;

4) a map f : X×[0, ∞] → R giving a time-varying con-

centration value of each position.

A feasible (suboptimal) solution is a set of pairs S⊆Msuch

that there exists at least a position x

(i ∈N, x

∈X, (i, x

) ∈

S), which satisﬁes that position x

lies in the vicinity of the

odor source, i.e., x

− x



<(the symbol ·

refers to a

Euclidean vector norm x

where x

∈Xdenotes the position

of the odor source, and the choice of  depends on applications).

A feasible solution S is optimal if the position x

is the position

of the odor source, i.e., x

− x

 =0.

Moreover, this type of optimization problem f(x

,t)(x

∈

X,t∈ [0, ∞]) has three main characteristics: 1) There exist a

global concentration maximum that is located in the position

of the odor source and multiple local concentration maxima

around the maximum; 2) the positions with local concentration

maxima are time varying; 3) odor concentration occurs within

a narrow region at each time, i.e., at a given time t, the odor

dispersion region X can be partitioned into two parts: X

and X

(X = X



) where f(x

,t) > 0,ifx

∈X

, and

f(x

,t)=0,ifx

∈X

. Fig. 1 shows an instantaneous plume

according to an odor model proposed by Farrell et al. [9]. In this

ﬁgure, an arrow denotes the speed and direction of the wind.

The position of the odor source is located at (10 m, 0 m), and the

search area is limited at 100 m × 100 m. Fig. 2 shows that the

剩余12页未读，继续阅读

评论收藏

内容反馈

weixin_38581447

粉丝: 8
资源: 911

一组机器人的决策和有限时间运动控制

气味源定位的有限时间运动控制策略

机器人的鲁棒有限时间控制方法

基座与臂杆全弹性空间机器人的有限时间控制.pdf

基于极坐标的非完整移动机器人运动目标跟踪的有限时间切换控制

轮式足球机器人决策部分

基于STM32的六足机器人运动控制系统研究.pdf

基于有限状态机的类人足球机器人决策系统设计.pdf

【机器人学习】SCARA机器人正逆运动学分析与直线轨迹规划（关节空间轨迹规划和笛卡尔空间轨迹规划）.rar

浅谈工业机器人技术在自动化控制领域的实践.pdf

基于领航跟随的多机器人系统有限时间一致性控制研究.pdf

机器人系统有限时间自适应迭代学习控制.pdf

存在死区的双柔杆空间机器人有限时间控制与抑振.pdf

有限时间切换控制扩展非完整链式系统的运动目标跟踪

线性多主体系统的有限时间编队控制：一种运动计划方法

智能水下机器人控制技术与发展趋势.pdf

《微型机器人设计》教学教案—嵌入式微型机器人直线运动控制.pdf

分布式多机器人运动控制的离散事件系统方法.pdf

改进多目标PSO算法优化机器人轨迹跟踪模糊PID控制器.pdf

创新之星追光机器人.doc

主-从自治海上航行器有限时间同步运动控制

基于运动规划方法的车辆有限时间编队跟踪控制

漂浮基空间机器人的全局鲁棒有限时间轨迹跟踪控制.pdf

机器人设计、组装和调试.rar

足球机器人智能决策系统设计实现.docx

RoboCup中型组机器人足球相关技术研究.pdf

Zynq软硬件平台的仿人机器人逆运动学求解系统.pdf

FIRA足球机器人仿真比赛DLL及源代码

最新资源