没有合适的资源?快使用搜索试试~ 我知道了~
众所周知,通过Sine-Liouville算子的缩合描述了SL(2,α)/ U(1)雪茄几何形状的非扰动α'校正,该运算符可以示意性表示为W + + W-,其中 W±描述一个绕数为±1的弦。 这种凝结导致雪茄几何形状产生有趣的影响,这种影响已经发生在弦理论的经典水平上。 在Lorentzian SL(2,ℝ)/ U(1)黑洞中解析连续Sine-Liouville算子的凝聚是有问题的。 在此,我们建议在黑洞情况下,根据算子来描述非扰动α'校正,该算子可以看作W +和W-融合的解析连续性。 我们表明,该算子不会遇到与分析上继续的Sine-Liouville算子相同的问题,并认为它描述了折叠的字符串,这些字符串填充了整个黑洞,并在某种意义上替代了黑洞的内部。 我们估计折叠后的琴弦辐射,并证明它们在霍金温度下辐射。
资源推荐
资源详情
资源评论

JHEP11(2019)014
Published for SISSA by Springer
Received: September 5, 2019
Revised: October 27, 2019
Accepted: October 27, 2019
Published: November 5, 2019
Stringy black hole interiors
Amit Giveon
a
and Nissan Itzhaki
b
a
Racah Institute of Physics, The Hebrew University,
Jerusalem 91904, Israel
b
Physics Department, Tel-Aviv University,
Ramat-Aviv, 69978, Israel
E-mail: giveon@mail.huji.ac.i, nitzhaki@post.tau.ac.il
Abstract: It is well known that non-perturbative α
0
corrections to the SL(2, R)/U(1) cigar
geometry are described via a condensation of a Sine-Liouville operator that schematically
can be written as W
+
+ W
−
, where W
±
describe a string with winding number ±1. This
condensation leads to interesting effects in the cigar geometry that take place already at the
classical level in string theory. Condensation of the analytically continued Sine-Liouville
operator in the Lorentzian SL(2, R)/U(1) black hole is problematic. Here, we propose that
in the black hole case, the non-perturbative α
0
corrections are described in terms of an
operator that can be viewed as the analytic continuation of the fusion of W
+
and W
−
.
We show that this operator does not suffer from the same problem as the analytically
continued Sine-Liouville operator and argue that it describes folded strings that fill the
entire black hole and, in a sense, replace the black hole interior. We estimate the folded
strings radiation, and show that they radiate at the Hawking temperature.
Keywords: 2D Gravity, Black Holes, Black Holes in String Theory
ArXiv ePrint: 1908.05000
Open Access,
c
The Authors.
Article funded by SCOAP
3
.
https://doi.org/10.1007/JHEP11(2019)014

JHEP11(2019)014
Contents
1 Introduction 1
2 AdS
3
and (1.3) 3
3 The cigar and (1.3) 4
3.1 CFT point of view 5
3.2 Space-time point of view 6
4 Lorentzian black hole 8
5 Folded string radiation 10
1 Introduction
Non-perturbative α
0
corrections to the SL(2, R)/U(1) cigar geometry [1–5] are described [6–
12] in terms of a condensation of a Sine-Liouville operator, λ
W
(W
+
+ W
−
), where
W
±
= exp
±i
β
2πα
0
(x
L
− x
R
)
e
−
1
Q
φ
; (1.1)
φ is the linear dilaton direction, with a slope Q, x = x
L
+ x
R
is the Euclidean time
direction, with periodicity β,
1
and λ
W
is the size of the winding condensate. These stringy
corrections, that are referred to as the FZZ duality [6] (see also [7]), led [13–15] to intriguing
effects, already in classical string theory on the cigar.
The SL(2, R)/U(1) black hole (BH) geometry can be obtained from the cigar geometry
via an analytic continuation. This coset CFT is particularly interesting in string theory,
e.g. since it is obtained in the near horizon limit of k near extremal NS5-branes [16] (with
Q
2
= 2/k). It would be very helpful to understand the non-perturbative α
0
corrections
to near extremal NS5-branes; these could possibly teach us some general lessons about
horizons and BH interiors in string theory. Naively, we simply have to Wick rotate (1.1),
to obtain
W
±
= exp
±
β
2πα
0
(t
L
− t
R
)
e
−
1
Q
φ
, (1.2)
where t = t
L
+t
R
is the real time direction (t = ix), but a subtlety with the operators (1.2)
is that they are not mutually local with vertex operator that amount to energy eigenstates.
A seemingly orthogonal question about this model was raised recently; it is related to
the argument [17] that folded strings [18–20] are created classically inside the SL(2, R)/U(1)
1
In the superstring, (1.1) is an N = 2 Liouville superfield, with β =
2π
Q
√
2α
0
, while in the bosonic string
β =
2π
Q
p
2(1 + Q
2
)α
0
.
– 1 –
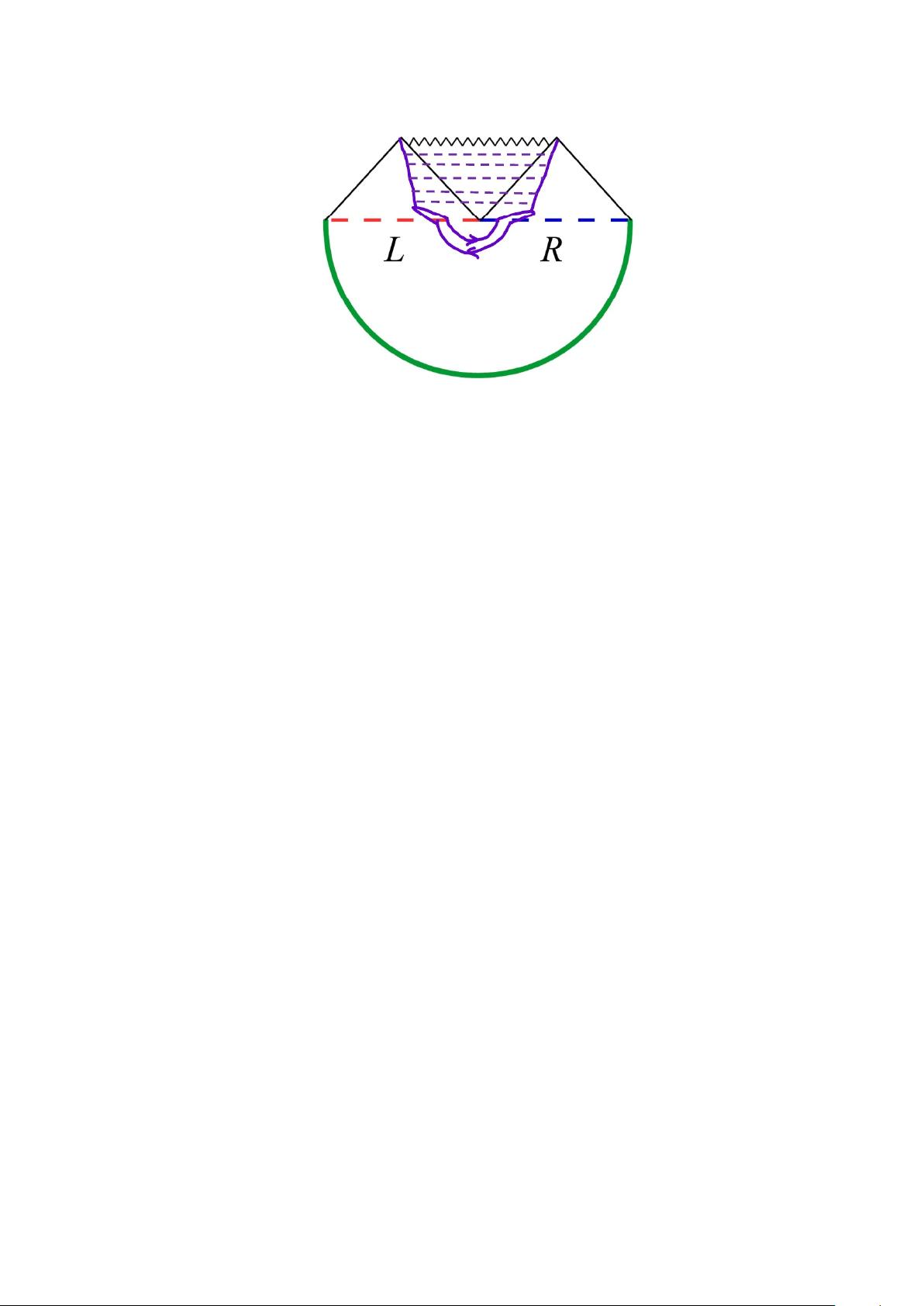
JHEP11(2019)014
Figure 1. The Hartle-Hawking wave function and the non-perturbative α
0
corrections. In the
Euclidean section there are strings with winding number ±1, denoted in the text by W
±
. They are
combined in the Lorentzian section to form a folded string, F , that can be viewed as a fusion of
W
+
and W
−
.
BH. If indeed there are classical folded strings inside the BH, then what is the operator in
the SL(2, R)/U(1) coset CFT that describes them?
The aim of this note is to address these questions. We recall [21–24] that, in addition
to (1.2), there is another non-perturbative (1,1) operator, denoted by F , whose underlying
AdS
3
parent is invariant under the SL(2, R)
L
×SL(2, R)
R
current algebra; thus, it condenses.
We argue that it amounts to the BH filling folded strings. F is not an ordinary vertex
operator; for example, it does not appear to be well defined for generic Q, and the size of
its condensate diverges for Q’s that amount to integer k’s. We show that these problems
are resolved by thinking about F as the fusion of W
+
and W
−
; schematically,
F ∼ W
+
∗ W
−
. (1.3)
We are thus led to suggest that, while in the cigar geometry the non-perturbative correc-
tions are described in terms of W
±
, when we analytically continue to the BH geometry, W
+
is combined with a W
−
to form an F (see figure 1), which describes the non-perturbative
α
0
corrections in the BH geometry. This is consistent with the fact that F is mutually local
with standard vertex operators in the BH geometry.
The rest of this note is organized as follows. In section 2, we discuss W
±
and F in
AdS
3
, and in section 3, we focus on the SL(2, R)/U(1) cigar. In particular, we show that
F is the fusion of W
+
and W
−
, and sharpen the relation between them both from the
CFT and space-time points of view. Moreover, we propose that while W
+
is the wave
function of the string condensate, and W
−
its conjugate, their fusion F can be viewed as
the probability density. Section 4 is devoted to the SL(2, R)/U(1) BH. There, we emphasize
the challenge in describing the non-perturbative α
0
effects using W
±
, and argue that F
should be identified with an interior filling folded string. In section 5, we estimate the
folded string radiation, and find it to be thermal with Hawking’s temperature.
– 2 –
剩余13页未读,继续阅读
资源评论

weixin_38521169
- 粉丝: 10
- 资源: 995
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功