独家Drell-Yan中大量夸克效应的分解和恢复资源-CSDN文库

Open

Access

130 浏览量 2020-03-24 03:31:05 上传评论收藏 1.71MB PDF 举报

资源推荐

资源详情

资源评论

JHEP08(2017)114

Published for SISSA by Springer

Received: April 6, 2017

Revised: July 18, 2017

Accepted: July 26, 2017

Published: August 25, 2017

Factorization and resummation for massive quark

eﬀects in exclusive Drell-Yan

Piotr Pietrulewicz,

Daniel Samitz,

Anne Spiering

and Frank J. Tackmann

Theory Group, Deutsches Elektronen-Synchrotron (DESY),

D-22607 Hamburg, Germany

Faculty of Physics, University of Vienna,

Boltzmanngasse 5, A-1090 Wien, Austria

Institut f¨ur Physik, Humboldt-Universit¨at zu Berlin,

Zum Großen Windkanal 6, D-12489 Berlin, Germany

E-mail: piotr.pietrulewicz@desy.de, daniel.samitz@univie.ac.at,

spiering@physik.hu-berlin.de, frank.tackmann@desy.de

Abstract: Exclusive diﬀerential spectra in color-singlet processes at hadron colliders are

benchmark observables that have been studied to high precision in theory and experiment.

We present an eﬀective-theory framework utilizing soft-collinear eﬀective theory to incorpo-

rate massive (bottom) quark eﬀects into resummed diﬀerential distributions, accounting for

both heavy-quark initiated primary contributions to the hard scattering process as well as

secondary eﬀects from gluons splitting into heavy-quark pairs. To be speciﬁc, we focus on

the Drell-Yan process and consider the vector-boson transverse momentum, q

, and beam

thrust, T , as examples of exclusive observables. The theoretical description depends on the

hierarchy between the hard, mass, and the q

(or T ) scales, ranging from the decoupling

limit q

 m to the massless limit m  q

. The phenomenologically relevant intermedi-

ate regime m ∼ q

requires in particular quark-mass dependent beam and soft functions.

We calculate all ingredients for the description of primary and secondary mass eﬀects re-

quired at NNLL

resummation order (combining NNLL evolution with NNLO boundary

conditions) for q

and T in all relevant hierarchies. For the q

distribution the rapidity

divergences are diﬀerent from the massless case and we discuss features of the resulting

rapidity evolution. Our results will allow for a detailed investigation of quark-mass eﬀects

in the ratio of W and Z boson spectra at small q

, which is important for the precision

measurement of the W -boson mass at the LHC.

Keywords: Jets, QCD Phenomenology

ArXiv ePrint: 1703.09702

Open Access,

 The Authors.

Article funded by SCOAP

https://doi.org/10.1007/JHEP08(2017)114

JHEP08(2017)114

So far, mass eﬀects from charm and bottom quarks in the initial state have been

discussed extensively for inclusive heavy-quark induced cross sections, leading to the de-

velopment of several variable-ﬂavor number schemes in deep inelastic scattering and pp

collisions (see e.g. refs. [12–18]). On the other hand, analogous heavy-quark mass eﬀects

from initial-state radiation have received little attention so far in the context of resummed

exclusive (diﬀerential) cross sections, i.e. where the measurement of an additional (diﬀer-

ential) observable restricts the QCD radiation into the soft-collinear regime requiring the

resummation of the associated logarithms. While e.g. for m  q

the mass eﬀects in the

resummed q

distribution are simply encoded by the matching between the parton distri-

bution functions across a ﬂavor threshold (e.g. matching four-ﬂavor PDFs onto ﬁve-ﬂavor

PDFs including a b-quark PDF at the scale m

, which happens much below the scale q

this description breaks down for q

∼ m or q

 m. A comprehensive treatment of these

regimes in resummed predictions has been missing so far. This concerns in particular also

parton-shower Monte-Carlo generators, which include massive quark eﬀects primarily as

kinematic eﬀects and by using massive splitting functions. Since heavy-quark initiated

corrections are one of the main diﬀerences between the W and Z boson spectra, this issue

can play therefore an important role for m

measurements at the LHC.

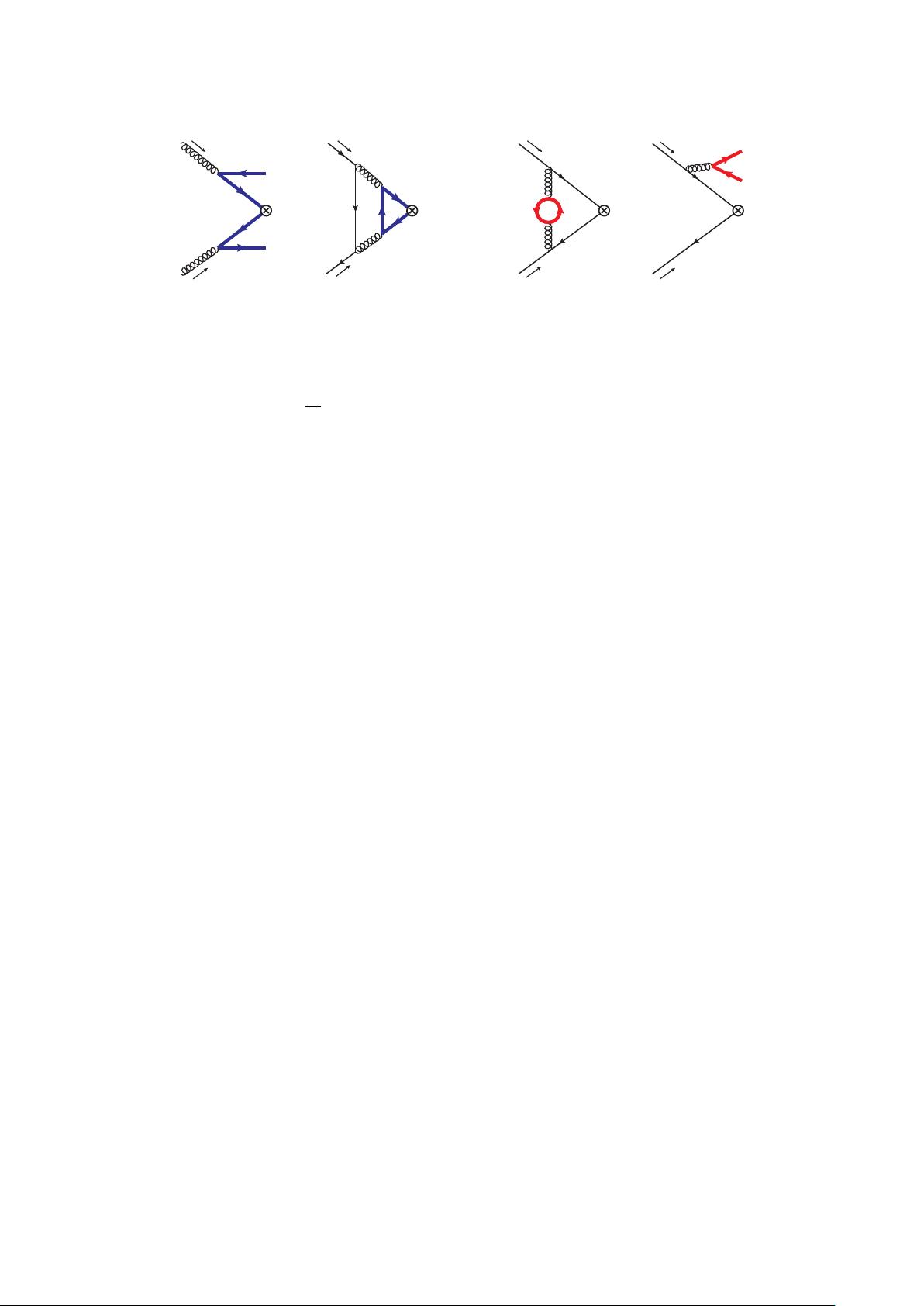
In general, one can distinguish two types of mass eﬀects as illustrated in ﬁgure 1,

which have diﬀerent characteristics: contributions where the heavy-quark enters the hard

interaction process are called primary mass eﬀects. Contributions from a gluon splitting

into a massive quark-antiquark pair with light quarks entering the hard interaction are

called secondary. For the q

spectrum, earlier treatments of the heavy-quark initiated

primary contributions for m . q

have been given in refs. [19–21], essentially combining the

ACOT scheme with the standard CSS q

resummation. A complete setup also requires to

account for secondary mass eﬀects. Their systematic description for diﬀerential spectra in

the various relevant hierarchies between mass and other physical scales has been established

in the context of event shapes in e

−

collisions [22, 23] and for threshold resummation

in DIS [24], see also refs. [25, 26] for a recent utilization in the context of boosted heavy

quark initiated jets. The application to diﬀerential spectra in pp collisions will be part of

the present paper.

We present a systematic eﬀective-theory treatment of quark mass eﬀects including both

types of mass eﬀects and all possible scale hierarchies using soft-collinear eﬀective theory

(SCET) [27–30]. We focus on the Drell-Yan process, pp → Z/γ

∗

→ `

−

, and consider two

types of observables that resolve additional QCD radiation and are used to constrain the

process to the exclusive region, namely the transverse momentum q

of the gauge boson

and beam thrust [31],

= |~q

| = |~p

T `

+ ~p

| =



T i



, T =

min{n

·p

, n

·p

}. (1.1)

Here, p

are all hadronic ﬁnal-state momenta (i.e. excluding the color-singlet ﬁnal state),

and n

a,b

= (1, ±ˆz) are lightlike vectors along the beam axes. Due to transverse momen-

tum conservation q

measures the total transverse momentum of the ﬁnal state hadronic

radiation, while beam thrust measures the momentum projections of all hadronic particles

– 2 –

JHEP08(2017)114

(a)

(b)

Figure 1. Primary (a) and secondary (b) heavy-quark mass eﬀects for Z-boson production.

onto the beam axis. The exclusive regime we are interested in corresponds to q

 Q or

T  Q, where Q =

is the dilepton invariant mass. These two observables restrict

the allowed QCD radiation into the collinear and soft regime in diﬀerent ways, leading

to diﬀerent eﬀective-theory setups with distinct factorization and resummation properties,

which are well-known in the massless limit up to high orders in the logarithmic counting

(see e.g. refs. [32–42] and refs. [31, 43, 44]). These two cases provide simple prototypical

examples, which cover the essential features of the factorization with massive quarks that

will also be relevant for including massive quark eﬀects for other more complicated jet

resolution variables whose factorization is known in the massless limit. Throughout the

paper we always consider the limit Λ

QCD

 q

, T allowing for a perturbative description

of the physics at these kinematic scales. We then consider all relevant relative hierarchies

between the heavy-quark mass m and the kinematic scales set by the measurement of q

or T , respectively.

In the second part of the paper, we explicitly compute all required ingredients for incor-

porating m

eﬀects at NNLL

order, which combines NNLL evolution with the full NNLO

singular boundary conditions (hard, beam, and soft functions). For Z-boson production at

NNLL

, primary eﬀects contribute via O(α

) ×O(α

) heavy-quark initiated contributions,

illustrated in ﬁgure 1(a). Secondary eﬀects contribute as O(α

) corrections to light-quark

initiated hard interactions, illustrated in ﬁgure 1(b). Due to the strong CKM suppression

primary m

-eﬀects do not play any signiﬁcant role for W -production, which represents a key

diﬀerence to Z-boson production. Primary m

-eﬀects enter W -production in the (sizeable)

cs-channel, where they start already at NLL

via O(α

) × O(1) corrections. For this case,

our explicit results for the regime q

∼ m

allows for up to NNLL resummation. (Here,

the resummation at NNLL

would require the O(α

) primary massive contributions.)

The paper is organized as follows: we ﬁrst discuss in detail the eﬀective ﬁeld theory

setup for the diﬀerent parametric regimes for the case of q

in section 2 and for T in

section 3. Here, we elaborate on the relevant mode setup in SCET, the resulting factoriza-

tion formulae, and all-order relations between the factorization ingredients in the diﬀerent

regimes. In section 4, we give the O(α

) and O(α

) results for the various ingredients

for NNLL

resummation. We also verify the consistency of our results with the associated

results in the massless limit. Further details on all calculations are given in the appen-

dices, where we also give the analytic results at ﬁxed-order for the massive quark eﬀects

– 3 –

剩余71页未读，继续阅读

评论收藏

内容反馈

weixin_38506798

粉丝: 4
资源: 937

独家Drell-Yan中大量夸克效应的分解和恢复

在TMD分解内，COMPASS上的非极化介子诱导的Drell-Yan过程中的布尔-莫尔德效应

Drell-Yan结构函数的扭曲分解：现象学意义

标准模型EFT和高能量Drell-Yan工艺

大型强子对撞机的Drell-Yan工艺违反R奇偶校验的限制

解开Drell-Yan生产的带有重味标记的Z'的耦合

带否决权的Drell-Yan过程：打破广义分解

Drell-Yan生产中的区域方法和近乎软校正

在双重Drell-Yan过程中取消了Glauber胶交换

在N3LO的Drell-Yan生产中领先的功率阈值校正

Drell-Yan过程中的壳外初始状态效应，量规不变性和角度分布

介子诱导的Drell-Yan过程的排他性极限

勘误到：从半包容性深部非弹性散射，Drell-Yan和Z-玻色子生产中提取部分横向动量分布

核Drell-Yan过程中夸克的能量损失 (2009年)

勘误表：LHC上Drell-Yan p T Z和ϕη*的NNLO QCD校正

从Drell-Yan / Z-玻色子生产中提取非极化的夸克横向动量相关的parton分布

介子在横向动量依赖分解中的介子诱导的Drell-Yan过程中的筛分不对称

减少高质量Drell-Yan谱中parton分布函数不确定性的新方法

扰动QCD中固定目标Drell-Yan实验的轻子角分布和几何方法

中不变质量和高横向动量下Drell-Yan过程的描述困难

TMD因式分解中介子诱导的Drell-Yan过程

Drell-Yan截面的Mellin矩的统一性方法

勘误到：通过光子融合和Drell-Yan过程产生单极子：MadGraph的实现和通过速度相关的耦合和磁矩的微扰性作为新功能

通过有限积分和一质量EW-QCD Drell-Yan主积分进行数值多回路计算

在s $$ \ sqrt {\ mathrm {s}} $$ = 13 TeV的质子-质子碰撞中差分Drell-Yan截面的测量

冷QCD物质和Drell-Yan过程的初始状态能量损失

在s = 8 TeV的质子-质子碰撞中测量微分和双微分Drell-Yan截面

最新资源