没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

A Gentle Introduction to Predictive Filters
Siome Klein Goldenstein
1
Abstract: Predictive filters are essential tools in modern science. They perform
state prediction and parameter estimation in fields such as robotics, computer vi-
sion, and computer graphics. Sometimes also called Bayesian filters, they apply the
Bayesian rule of conditional probability to combine a predicted behavior with some
corrupted indirect observation.
When we study and solve a problem, we first need its proper mathematical formula-
tion. Finding the essential parameters that best describe the system is hard, modeling
their behaviors over time is even more challenging. Usually, we also have an in-
spection mechanism, that provides us indirect measurements, the observations, of the
hidden underlying parameters. We also need to deal with the concept of uncertainty,
and use random variables to represent both the state and the observations.
Predictive filters are a family of estimation techniques. They combine the system’s
dynamics uncertain prediction and the corrupted observation. There are many differ-
ent predictive filters, each dealing with different types of mathematical representations
for random variables and system dynamics.
Here, the reader will find a dense introduction to predictive filters. After a general in-
troduction, we have a brief discussion about mathematical modeling of systems: state
representation, dynamics, and observation. Then, we expose some basic issues related
with random variables and uncertainty modeling, and discuss four implementations
of predictive filters, in order of complexity: the Kalman filter, the extended Kalman
filter, the particle filter, and the unscented Kalman filter.
1 Introduction
In applied sciences, we use mathematical models to describe, understand, and deal
with real objects. Applications are varied, and may involve guiding a mobile exploratory
vehicle, understanding a human face and its expressions, or controlling a nuclear power plant
reactor. A good mathematical representation lets us infer properties of the real entity, and
understand beforehand the possible implications of our interactions with it.
The state vector of a model is the set of parameters that uniquely describe a config-
uration of the object. The set of parameters that model an object is usually not unique, and
each situation leads to a different set of design choices. When the object’s parameters are not
1
Instituto de Computação, UNICAMP
Caixa Postal 6176, Campinas - SP, 13084-971 Brazil
siome@ic.unicamp.br

A Gentle Introduction to Predictive Filters
static, we also need a mathematical model for their change over time. We call a system, the
mathematical representation of states and dynamics.
Sometimes, the parameters we choose to represent a system are intrinsic to the prob-
lem but impossible to be measured, such as the temperature in the core of a nuclear power
plant. Fortunately, we can usually measure other quantities that are related to the unknown,
but essential parameter, such as the temperature of the cooling water leaving the core. These
indirect measurements are called observations, and can be used to infer information about
the hidden parameter.
Real life is hard, and full of errors. The observations we make are not precise, and they
may not explain all that is happening in the system. Also, our mathematical representation
of the model is not exact, giving slightly incorrect results. To cope with all these factors, we
need to incorporate the notion of uncertainties. There are many mathematical descriptions
for uncertainties, but in this paper we use probabilities.
Predictive filters estimate the optimal state of a system. First, they use the mathemat-
ical model of the system dynamics to propagate the state’s values and uncertainties. Later,
they combine this preliminary estimate and as much as it is possible from the observation.
There are several predictive filters, each appropriate for a different type of uncertainty repre-
sentation and dynamic modeling.
The Kalman filter is the simplest example of a predictive filter. It represents uncertain-
ties as Gaussian random variables, fully described by a mean and a covariance matrix, and
models the system with linear dynamics and observations. Since Gaussians are preserved
under linear transformation, the Kalman filter’s implementation uses only linear algebra op-
erations.
If we need more complex models to describe a system, we may have to use nonlin-
ear functions. The extended Kalman filter linearizes the system around the current state to
propagate and estimate covariance matrices.
We can represent the random variables as a collection of samples, and allow nonlinear
operations. In this case, we can use a particle filter, which is powerful and flexible. Unfortu-
nately, it needs an a number of samples exponentially related to the state’s dimension.
Here, the last predictive filter we talk about is the unscented Kalman filter. It uses
a small number of specially selected particles to propagate random variables over nonlinear
transformations.
In this paper, we follow the same type of structure of Maybeck’s classical book [20].
In Section 2, we deal with the problem of building a mathematical model that describes the
state of the system (Section 2.1), its dynamics (Section 2.2), and how to inspect it at every
moment (Section 2.3). Then, in Section 3, we review uncertainties: probabilities and random
2 RITA • Volume • Número • 2004

A Gentle Introduction to Predictive Filters
variables. Finally, in Section 4, we describe the Bayesian concepts of predictive filters, and
look at some of its concrete implementations: the Kalman filter (Section 4.1), the extended
Kalman filter (Section 4.2), the particle filter (Section 4.3), and the unscented particle filter
(Section 4.4). In Section 5, we conclude this paper with a series of words of caution, as well
as a series of pointers to where the reader can find more information.
2 System Representation
Predictive filtering techniques rely on a mathematical representation of the system. In
this section, we discuss how to model a system’s parameters and their dynamical aspects, and
how to describe our indirect ability to inspect them.
A system is just like a black box, controlled by a set of parameters. To manipulate
and understand a system, we need a mathematical model that describes these parameters and
their behavior over time.
There are three general guidelines to modeling: first, the mathematical model should
be as precise as possible – the system’s behavior model should be as close as possible to
reality. Second, the model should be tractable – we need to handle the mathematical model
in a efficient way. Finally, the model should be as simple as possible – there is no need to
describe a detail of the system, if this detail holds no consequence to the desired application.
Usually, these three guidelines are incompatible, and we have to strike a balance. In the next
three sections we describe the ideas behind state description, the observation procedure, and
the dynamic behavior.
2.1 State Description
We use several real-valued variables to describe a system state.
2
If we use n parame-
ters to describe the system, we group them in a vector
~x
t
∈ R
n
,
that uniquely identifies the system’s situation at time t. We now look at two examples.
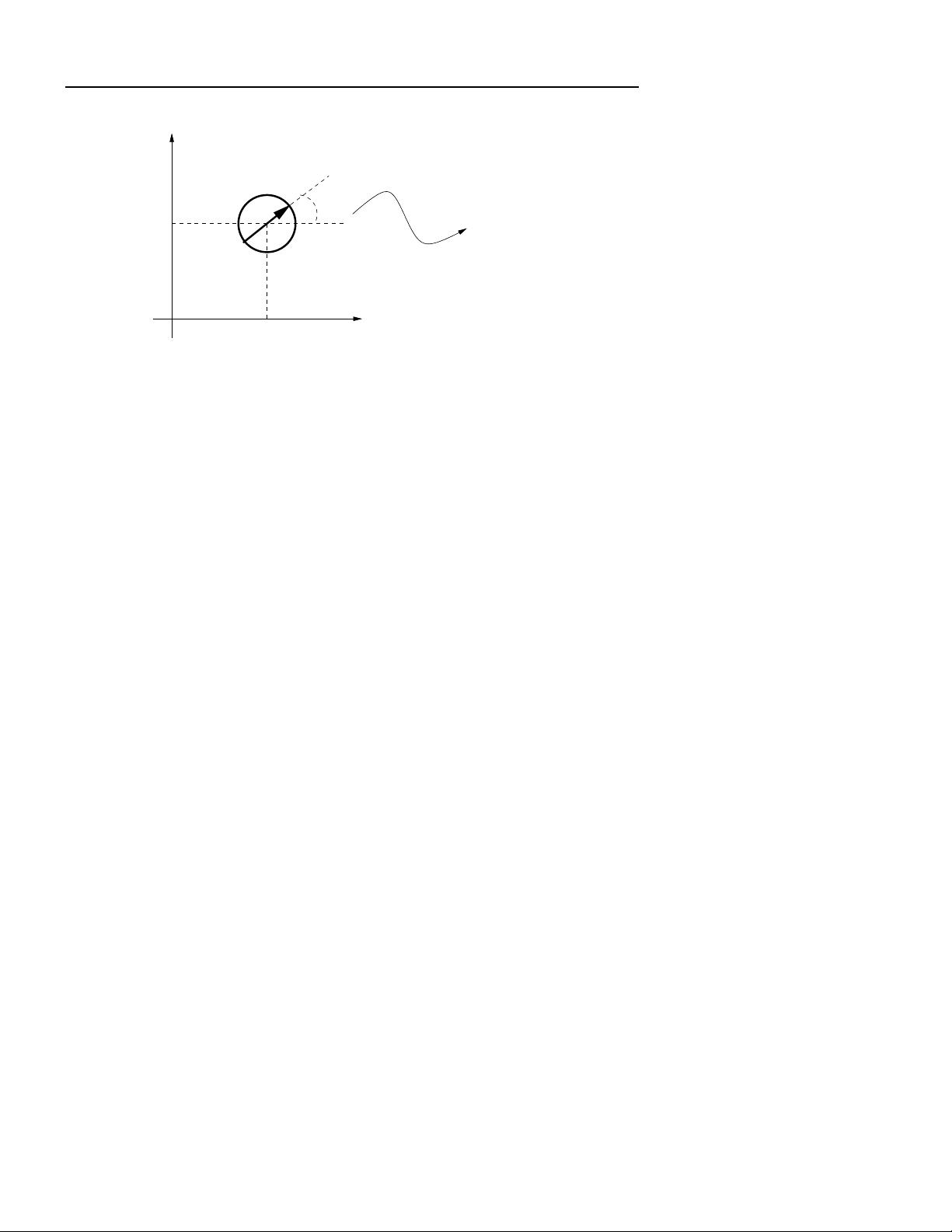
Example 1: Simple Robot Lets consider a mobile robot, that can turn around its axes and
move in the forward direction. We know that the robot cannot leave the floor, so we only
need two coordinates to describe its position. We also need a third parameter to describe its
facing direction. This is illustrated in Figure 1.
2
It is possible, and sometimes more adequate, to model systems with graphs and discrete variables, but that is beyond
the scope of this paper.
RITA • Volume • Número • 2004 3
A Gentle Introduction to Predictive Filters
PSfrag replacements
x
y
θ
~x =
x
y
θ
Figure 1. A simple state model of a robot, with x and y positions and forward direction θ.
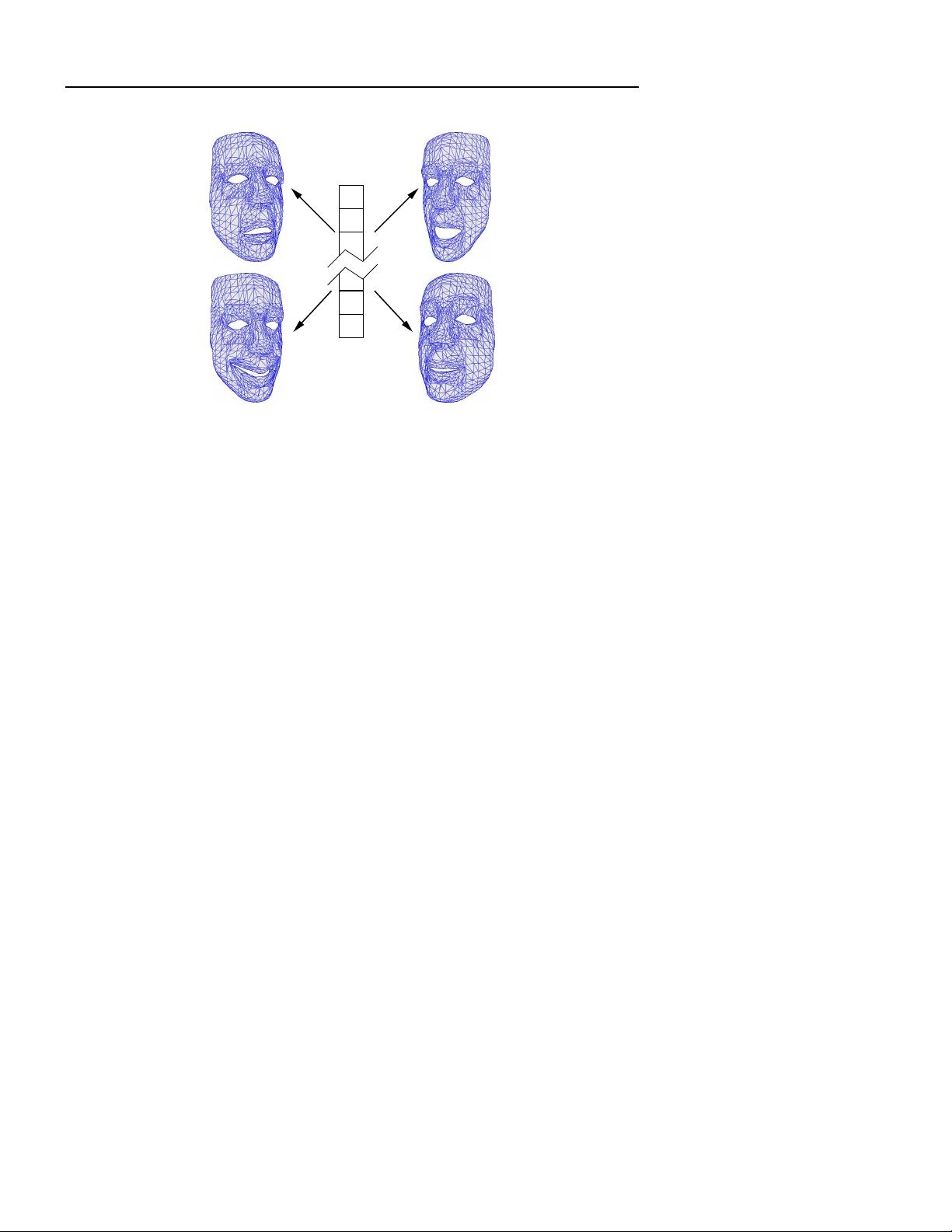
Example 2: Human Face When we look at a human face as a system, we can model de-
formation parameters. These parameters describe the effects of the muscles’ action on the
surface of the face. In Figure 2 we see an illustration of how the state vector can affect the
overall shape and position of a face.
2.2 Dynamic Behavior
In order to describe the dynamic behavior of a system, we take into account its state
history and some external inputs, represented as ~u
k
∈ R
l
. In control theory, we use the
mathematical model, along with the initial configuration of the state, to plan the input ~u
over time. This planned ~u guides the system’s state according to our goals. In Bayesian
state estimation, we do not know what the inputs really are (perhaps just some statistics), but
estimate the best state configuration using indirect observations.
There are two models for the passage of time, continuous and discrete. In the first one,
time is a value t ∈ R. In the second representation, time is a integer variable k ∈ Z. Usually,
the discrete time approach is considered an uniform sampling t = k · ∆T of the continuous
case. In this paper, we will only use the discrete representation.
A natural representation for the dynamics of discrete-time system is a difference equa-
tion. The next state depends on the current input and all the system’s history
~x
k+1
= f (~u
k
, ~x
k
, . . . , ~x
0
) .
Fortunately, it is usually enough to consider that the next state depends only on the
4 RITA • Volume • Número • 2004
A Gentle Introduction to Predictive Filters
PSfrag replacements
~x =
x
0
x
1
x
n−1
x
n
Figure 2. The state space of a deformable face describes the global position and orientation,
as well as local changes such as eyebrow movement, jaw and lip movement.
current state and the external input
~x
k+1
= f (~u
k
, ~x
k
) , (1)
where f : R
l
× R
n
→ R
n
. If the system needs to take into account more past states, we use
state enhancing techniques (Section 2.2.2) to be able to still use this simplification.
2.2.1 Linear Modeling In linear systems, the model of dynamics is a linear combination
of the past state and the external inputs. Linear systems are mathematically easy to deal
with, usually providing us with analytical and well behaved solutions, and have efficient
implementations. Sometimes it is possible to design the system’s state variables to allow the
use of a linear dynamics.
Example: One-dimensional uniform motion. In this case, the state vector is
~x =
x
v
,
where x is the position, and v the velocity. The dynamics can be represented as a simple
matrix multiplication
~x
k+i
=
1 ∆T
0 1
~x
k
.
RITA • Volume • Número • 2004 5
剩余28页未读,继续阅读
资源评论

chi_mian
- 粉丝: 10
- 资源: 5
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 高校毕业生就业信息-JAVA-基于springboot的高校毕业生就业信息管理系统(毕业论文)
- node-red-contrib-opcua-test.json
- 高校社团管理-JAVA-基于springBoot的高校社团管理系统的设计与实现(毕业论文)
- 基于pytorch实现的ghostnetv1、v2、v3对10种鸟类图像识别【完整代码+数据集】
- 医疗设备管理-JAVA-基于springboot的医疗设备管理系统设计与实现(毕业论文)
- 基于AT89C52单片机的6位电子密码锁设计-14.zip
- 解决用STM32CubeMX配置FreeRTOS时头文件丢失问题
- 古城景区-JAVA-基于Spring Boot的古城景区管理系统的设计与实现(毕业论文)
- 2024全国大学生软件测试大赛Web赛项-省赛真题
- 商用密码,我国商用密码行业发展介绍
- 交通旅游订票-JAVA-基于spring boot的交通旅游订票系统设计与实现(毕业论文)
- 商用密码法律法规及标准体系解读V1.8-240827
- 流浪动物救助-JAVA-基于spring boot的流浪动物救助系统的设计与实现(毕业论文)
- Hadoop与Spark集群搭建及中文字频统计与Titanic数据分类实战
- 中国飞行器设计大赛圆筒权重文件
- 学生成绩管理-JAVA-基于spring boot的软件学院学生成绩管理系统的设计与实现(毕业论文)
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功