现代控制理论基础2015(A卷)--答案1

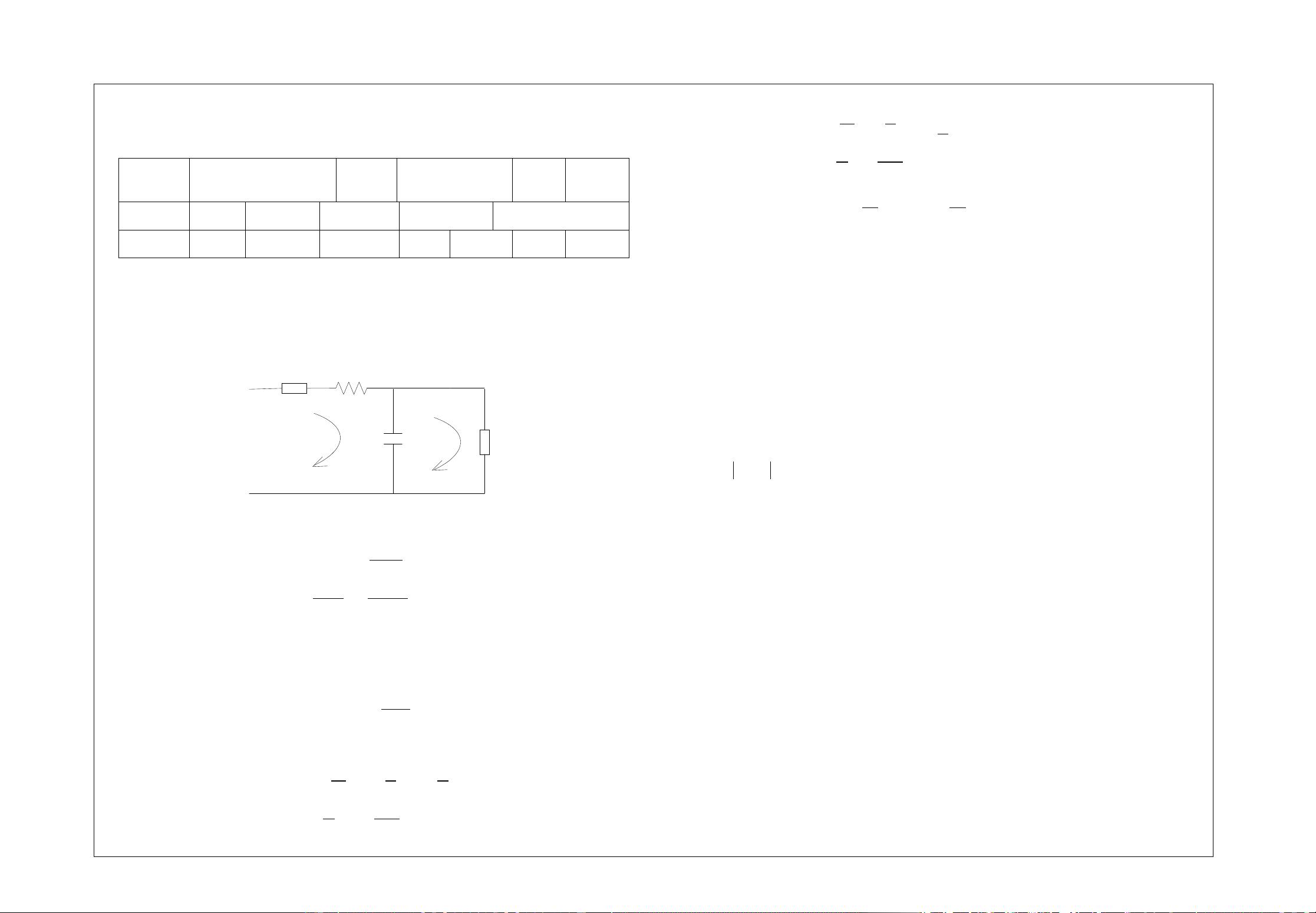
现代控制理论基础是自动化、电气工程等相关专业的重要课程，它主要研究如何设计和分析控制系统以确保其稳定性和性能。这份2015年的A卷考题涵盖了线性定常连续系统的多个方面，包括状态空间表示、系统特征分析、状态转移矩阵的计算以及线性变换对系统特性的影响。 在第一个问题中，题目要求对一个RLC系统建立状态空间模型。状态空间模型是一种描述系统动态行为的方法，通过一组状态变量来表示系统的内部动态过程。在这个例子中，输入是电流源\( u(t) \)，输出是电流\( i_2(t) \)，状态变量选为电感电流\( i_1(t) \)和电容电压\( x_1(t) \)。经过微分方程的推导，得到了系统的状态方程和输出方程，最终以矩阵形式表示了这个RLC系统的状态空间模型。 第二个问题涉及到线性定常连续系统的特征分析。给定系统由状态矩阵\( A \)、输入矩阵\( B \)和输出矩阵\( C \)定义。要求求解特征多项式、特征值和状态转移矩阵。特征多项式是由\( A \)的行列式得到，特征值是使特征多项式为零的\( s \)的值。特征值对系统的稳定性至关重要，而状态转移矩阵\( \Phi(t) \)描述了系统从一个初始状态到任意时间\( t \)的状态演变。 第三个问题是关于线性变换对系统特性的影响。如果对状态变量进行线性变换\( x = P^{-1}x' \)，那么原系统\( \Sigma(C,A,B) \)在新状态变量下的表示为\( \Sigma'(C',A',B') \)。在这里，\( A' \)、\( B' \)和\( C' \)可以通过矩阵\( P \)与原矩阵的关系来确定。变换前后系统的传递函数保持不变，这表明系统的动态特性在状态变量变换后并不会改变。 这份试卷考察了学生对线性定常连续系统基本概念的理解，包括状态空间建模、系统特性分析以及线性变换的性质。这些问题的解答需要扎实的数学基础，尤其是线性代数和微积分的知识，同时还需要理解控制系统理论的基本原理。通过解决这些问题，学生可以深入掌握现代控制理论的基础，并能应用这些理论解决实际的控制工程问题。