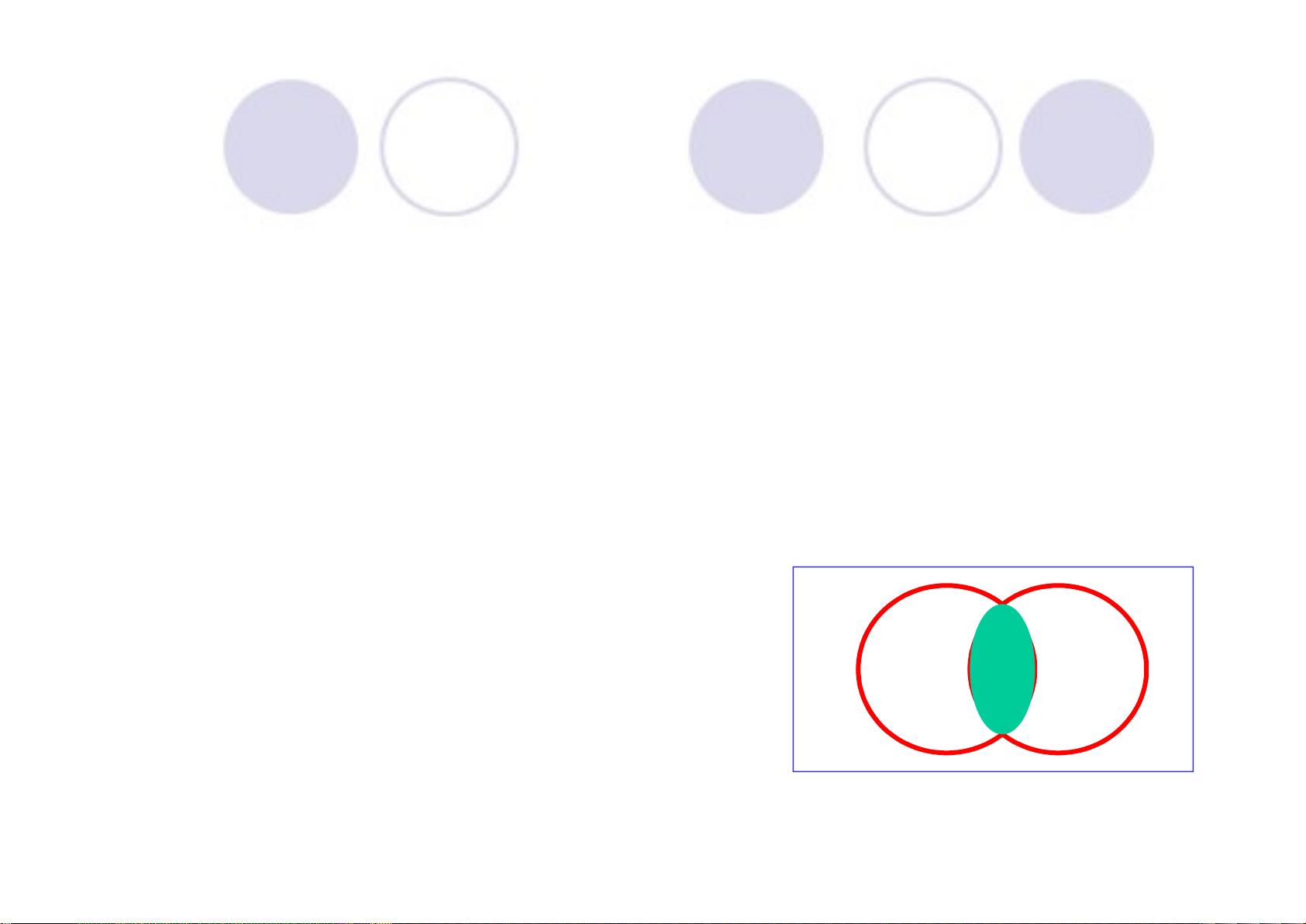
集合论是数学的基础概念之一，主要研究集合以及与集合相关的操作。在本节中，我们将深入探讨三种基本的集合运算：相交运算、联合运算（集合的并）以及差分运算（集合的补）。
相交运算指的是取两个集合A和B的公共元素组成的集合，记作A∩B。例如，如果A={a, b, c, d}，B={d, f, a}，那么A∩B={a, d}。交集运算具有以下性质：A∩A=A，A∩∅=∅，A∩B=B∩A，并且对于任何集合C，A∩(B∪C)=(A∩B)∪(A∩C)，这被称为交集的分配律。
接着，我们来看联合运算，即取两个集合A和B的所有元素组成的集合，记作A∪B。比如，如果A={a, b, c}，B={c, d, f}，那么A∪B={a, b, c, d, f}。联合运算同样有其特性：A∪A=A，A∪∅=A，A∪B=B∪A，且对于任何集合C，A∪(B∩C)=(A∪B)∩(A∪C)，这是并集的分配律。
差分运算，又称集合的补，是取集合A中不属于另一个集合B的元素，记作A-B或AΔB。若A={a, b, c}，B={b, c, d}，则A-B={a}，因为a是A中不在B内的唯一元素。差分运算体现了集合中元素的排除。
对于多个集合的交集或并集，我们可以使用类似的方法扩展这些运算。例如，如果有三个集合A，B，C，它们的交集可以表示为A∩(B∩C)，而它们的并集可以表示为A∪(B∪C)。当有n个集合时，我们可以用类似的方式进行组合，如A1∩A2∩...∩An和A1∪A2∪...∪An。
在实际问题中，集合论的应用广泛。例如，问题中的学生可能误解了集合交集和并集的概念，将运动项目混淆了。A∩B应该是参加两种比赛的共同同学，而A∪B是所有参赛者，无论是参加哪项比赛。
总结起来，集合论的基本运算包括相交、并集和差分，它们是理解和解决各种数学问题，尤其是离散数学问题的关键工具。通过深入理解这些运算及其性质，我们可以更好地处理数据、定义关系和解决问题。在信息技术、计算机科学和数学领域，这些基础知识有着至关重要的作用。
评论0