大连理工大学软件学院离散数学集合论2nd公开课获奖课件.pptx
离散数学中的集合论是计算机科学的基础,尤其对于理解数据结构、算法以及逻辑推理至关重要。在大连理工大学软件学院的这堂公开课中,讲师深入讲解了集合论的基本概念和运算。 集合是一个基本的数学构造,它是由一些明确确定的对象组成的整体,这些对象称为集合的元素。集合的定义是通过其元素的内涵和外延来确定的。内涵指的是集合的性质,而外延则是集合的实际元素。例如,所有大于10的素数组成的集合的内涵是“大于10的素数”,外延则是{11, 13, 17, ...}。 集合的基数是集合中元素的数量。集合间的关系包括相等、包括(或包含)和真包括。两个集合相等如果它们的元素完全相同;一个集合A包括另一个集合B,如果B的所有元素都在A中;真包括是指B的所有元素都在A中,但A可能有B没有的元素。 差分运算(集合补)是集合运算的一种,它找出属于A但不属于B的所有元素。记作A-B,表示A与B的差集。例如,如果A是大于等于10的素数集合,B是奇数集合,那么A-B就是只属于A不在B中的元素,即{2}。集合的绝对补集是相对于全集E的补集,记作~A,表示不在集合A中的所有元素。 集合的差分运算具有若干性质,例如A-A等于空集,表明一个集合与自身的差集为空。此外,还有一些涉及集合差分运算的定理,如定理3.2-4和定理3.2-5,这些定理提供了关于集合差分运算的进一步关系。 对称差分运算定义为A和B的所有元素中,既属于A又不属于B的,或者属于B但不属于A的元素的并集,记作AΔB。例如,如果A={1,2,3},B={3,2,4},那么AΔB={1,4}。对称差分运算满足交换律和分配律等性质。 集合定律是集合论中的核心部分,包括并、交、差等运算的结合律、分配律等。例如,假设A、B和C是任意三个集合,那么(A∪B)∪C=A∪(B∪C),这是并运算的结合律。类似地,对交运算也有类似的结合律。还包括De Morgan定律,它描述了集合的补集与并、交运算的关系。 包括排斥原理是集合论中的一个重要原理,适用于有限集合。如果A1和A2是两个有限集合,那么它们的基数之和减去它们的交集的基数,等于它们并集的基数。这可以用公式表示为|A1∪A2|=|A1|+|A2|-|A1∩A2|。这个原理在解决有关存在性和计数的问题时非常有用。 这堂公开课深入浅出地讲解了集合论的基础知识,包括集合的概念、基数、集合的关系、差分运算、对称差分运算以及集合定律,这些都是学习离散数学和计算机科学所必需的基础。通过理解和掌握这些内容,学生能够更好地理解数据结构、算法和逻辑推理,为后续的编程和理论研究打下坚实基础。




剩余34页未读,继续阅读

- 粉丝: 802
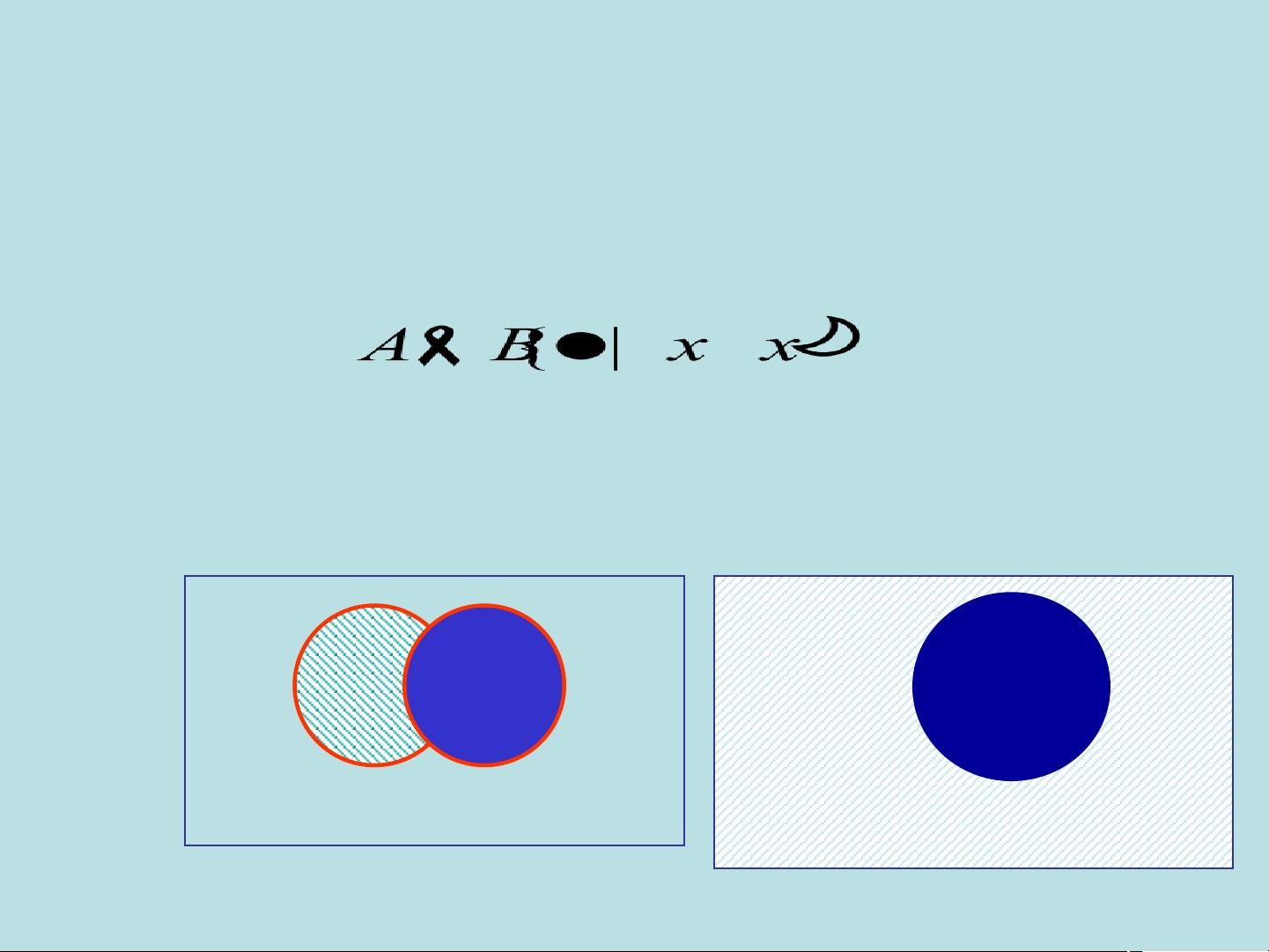
- 资源: 7万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功