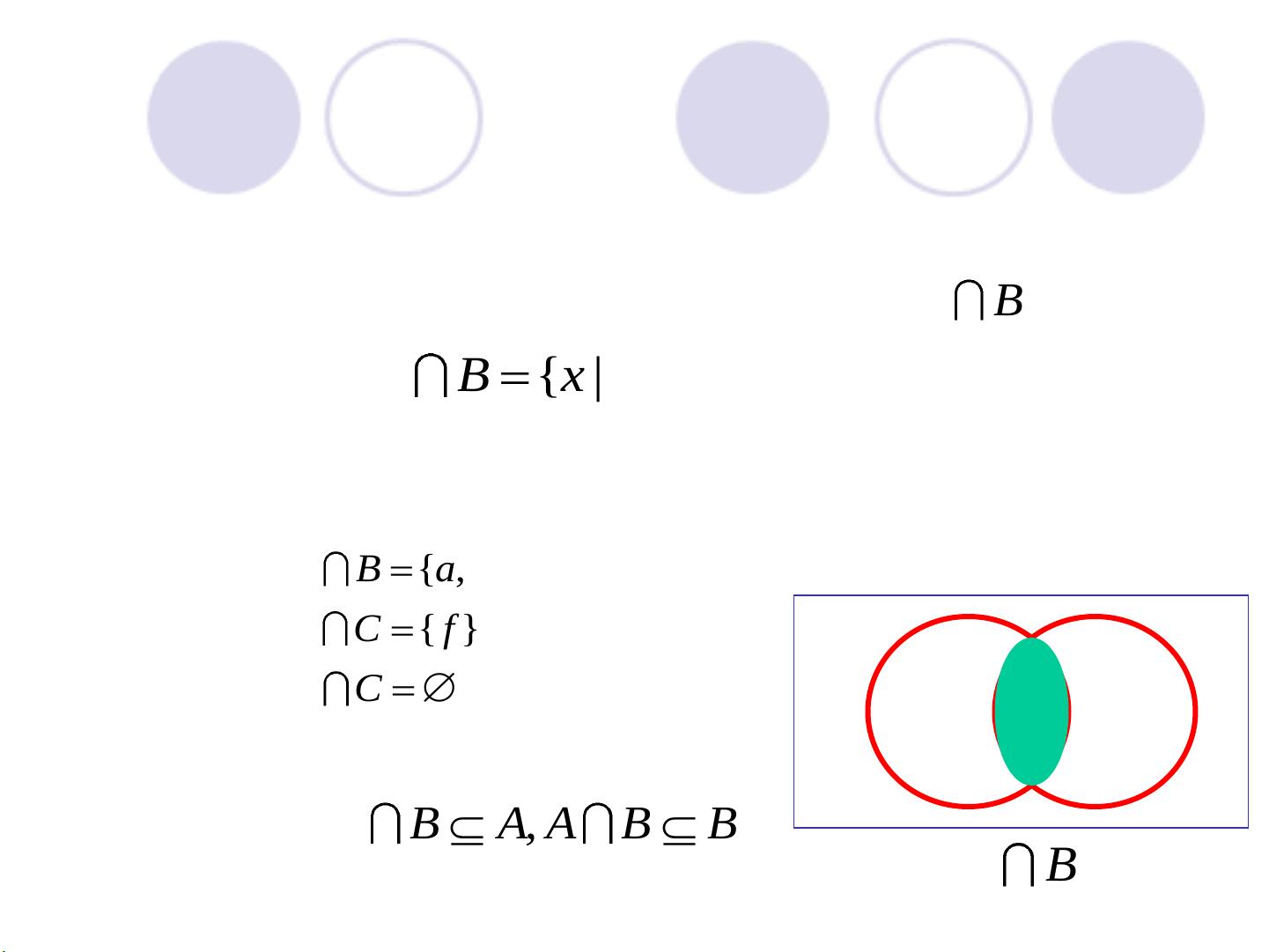
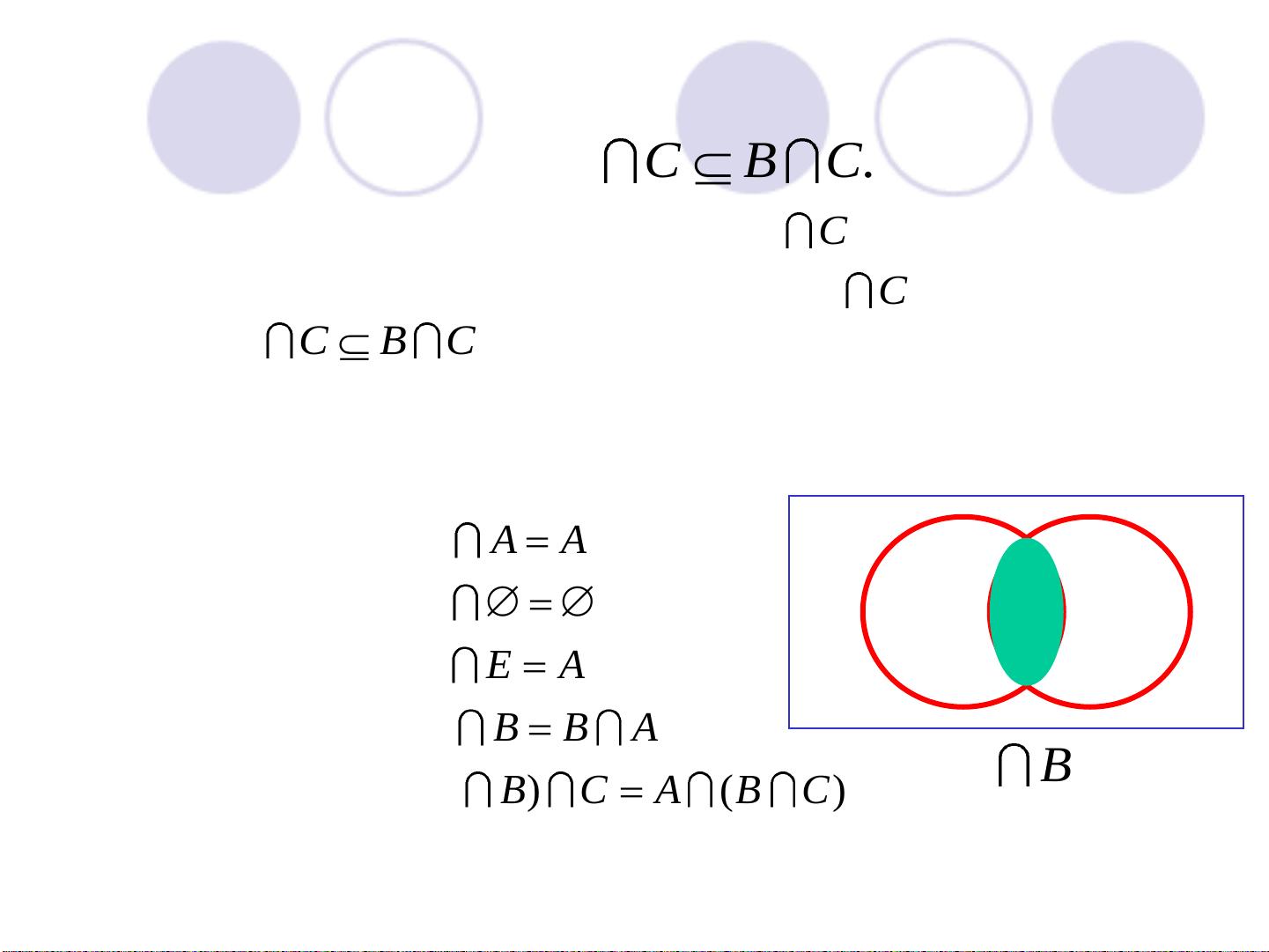
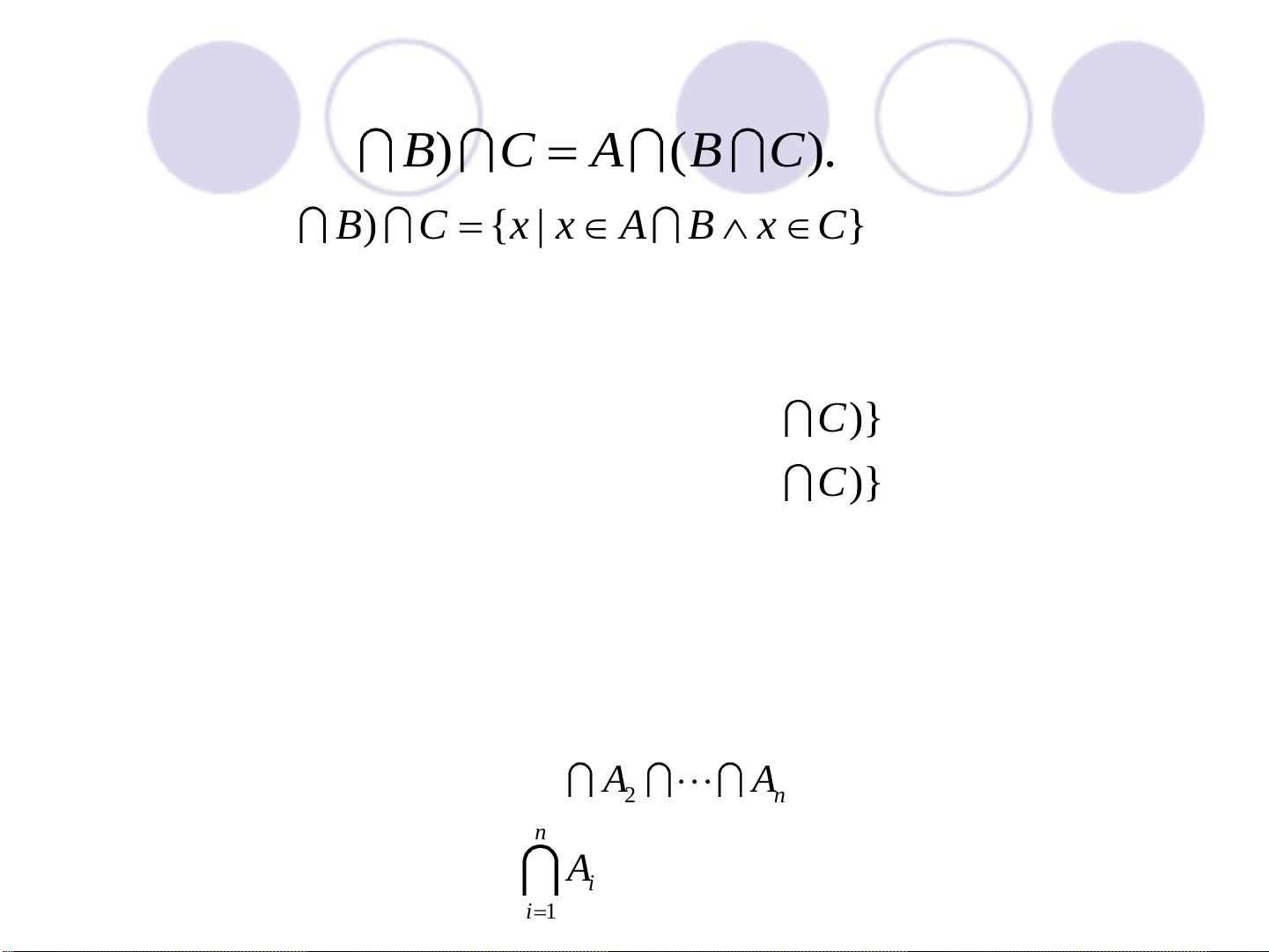
在离散数学中，集合论是基础理论之一，它研究集合以及它们之间的关系和运算。在本章"第3章 集合论-2nd1"中，主要讨论了两个核心概念：集合的运算，具体包括相交运算和联合运算。
相交运算描述了两个集合共享的元素。如果集合A和B的交集记为AB，那么它是所有既属于A也属于B的元素的集合。例如，给定集合A={a, b, c, d}和B={d, f, a}，它们的交集AB={a, d}。证明交集的性质时，我们可以看到，如果A⊆B，那么AB=B。此外，多个集合的交集也满足结合律，即无论括号如何放置，结果保持不变。
接下来是联合运算，也称为并集，它包含来自两个集合的所有元素，不论这些元素是否相同。例如，集合A={a, b, c}和B={c, d, f}的并集AB={a, b, c, d, f}。集合的并运算具有与交集不同的性质，如A∪∅=A，A∪A=A，以及A∪B=B∪A等。同样，多个集合的并集依然遵循结合律。
此外，我们还学习了如何处理三个或更多集合的交集和并集。比如，设A, B, C为三个集合，根据定理3.21，我们知道(A∪B)∪C=A∪(B∪C)，这表明并集运算满足结合律。类似地，定理3.22说明了(A∩B)∩C=A∩(B∩C)，交集运算也保持结合律。而定理3.23指出，集合A与B的并集等于B与A的并集，即A∪B=B∪A，这体现了并集的交换律。
在实际应用中，例如在体育赛事中，如果我们有集合A，其中元素代表参加百米赛跑的同学，集合B代表参加跳高的同学，那么A∪B将包含所有参加百米赛跑或跳高比赛的同学，而A∩B则会是同时参加这两项比赛的同学。
通过深入理解集合的交集和并集，我们可以更好地分析和表达数学、计算机科学以及其他领域中的复杂关系和数据结构。这些基本概念是构建更高级的数学理论和算法的基础，对于理解和解决实际问题至关重要。
评论0