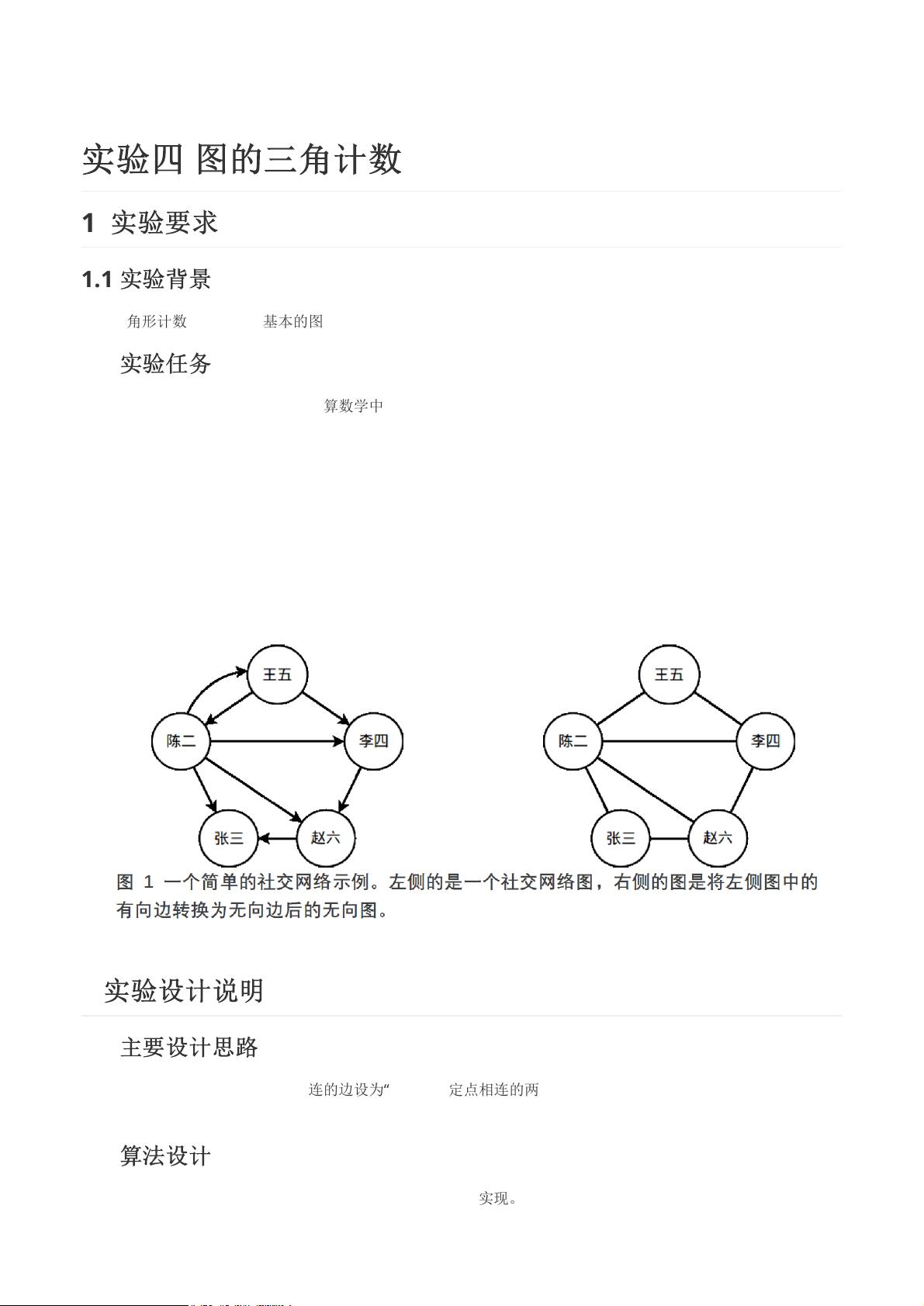
实验四 图的三角计数1

【实验四 图的三角计数1】实验主要探讨的是如何在社交网络图中计算三角形的数量，这是一个在图论和复杂网络分析中的基础问题。在社交网络如Twitter中，用户之间的关注关系可以抽象成图的有向边。实验的具体任务是将这些有向边转化为无向边，并统计形成的无向图中所有三角形的数量。 实验要求理解图的三角形计数的重要性，特别是在社交网络分析中，它可以帮助我们理解用户之间的交互模式和社区结构。一个三角形代表三个用户彼此相互关注的关系，这在社会网络中可能意味着更紧密的联系或共同的兴趣。 实验设计思路如下： 1. 将有向边转化为无向边，确保边的方向不影响三角形的计算。 2. 使用MapReduce框架来执行计算，该框架适用于大规模分布式计算。实验共分为三个阶段（Job）： - 第一次MapReduce（Map_1和Reduce_1）：读取原始数据，处理边的方向，确保键值对形式为(A+B, +)，并去重。 - 第二次MapReduce（Map_2和Reduce_2）：检查是否存在三角形，若存在AB和AC边，则记录(A+B, +)和(A+C, +)，同时检查BC边，若存在则记录(B+C, -)。 - 第三次MapReduce（Map_3和Reduce_3）：计算每个边参与的三角形数量，通过累加以某条边为边界的三角形个数来得到总三角形数。 在代码实现部分，Map_1 和 Reduce_1主要负责数据预处理，Map_2 和 Reduce_2负责构建无向边并标记可能的三角形，而Map_3 和 Reduce_3则完成最终的三角形计数。在Map函数中，数据被分割并处理，而在Reduce函数中，数据被聚合和计算。 例如，Map_1读取输入数据，比较两个顶点的顺序，确保A<B，并输出(A+B, +)的形式。Reduce_1则负责去重，确保每个无向边只出现一次。Map_2和Reduce_2进一步处理这些数据，构建无向边的表示，并在发现三角形时记录(-)的边。Map_3不改变数据，Reduce_3则计算三角形的数量。 这个实验不仅涵盖了图的理论知识，还涉及到了分布式计算的实际应用，特别是MapReduce模型的运用，这对于理解和解决大数据环境下的图计算问题具有重要意义。通过这个实验，学生可以深入理解社交网络的结构特性，并掌握利用编程技术进行复杂网络分析的基本技能。