蚁群算法的随机Petri网分析与路径寻优1

本文主要探讨了在随机Petri网（Stochastic Petri Net, SPN）环境下，如何利用蚁群算法进行路径寻优。随机Petri网是一种扩展的Petri网模型，其中每个变迁的执行时间不再是一个固定的延迟，而是遵循一定的概率分布。这种模型更真实地反映了实际系统中存在的时间不确定性。 文章介绍了Petri网中时间概念的发展，从最初的固定延迟到随机延迟的概念。在随机Petri网中，变迁的实施时间具有随机性，这使得分析和优化网络行为变得更加复杂。为了应对这一挑战，作者提出了一个计算SPN中变迁时间概率分布的方法，这有助于理解和预测系统的动态行为。 接着，文章提出了一种基于蚁群算法的路径寻优策略。蚁群算法是一种模拟蚂蚁寻找食物路径的优化算法，常用于解决组合优化问题，如旅行商问题。在SPN的背景下，每个变迁和库所被赋予特定的数据结构，使得算法能够有效地处理时间延迟和概率分布信息。通过信息素的动态更新和浓度调整，算法能够在搜索过程中兼顾局部最优和全局最优，从而提高路径寻优的效率和准确性。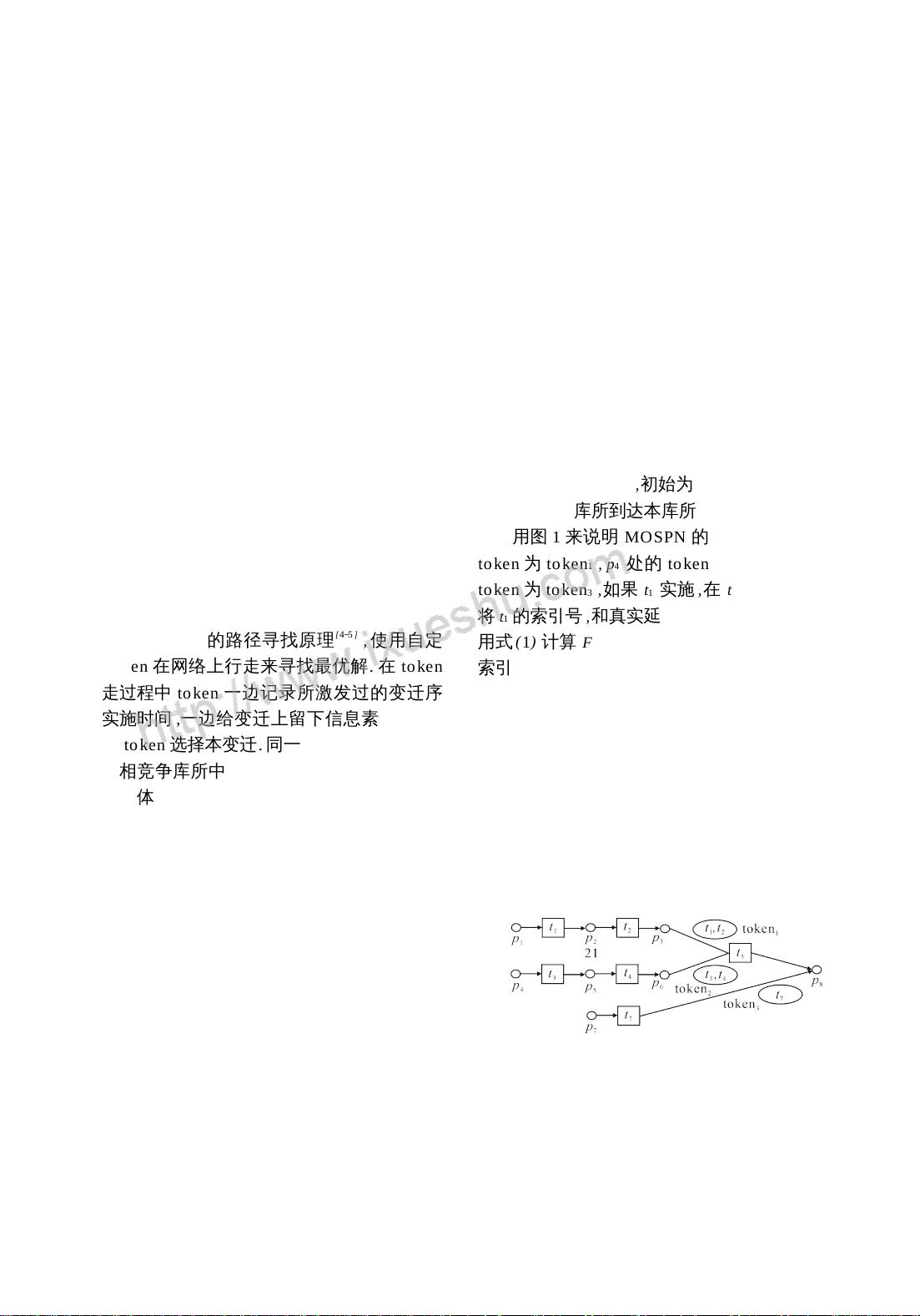 具体来说，当一个token（在Petri网中代表活动的单元）找到一条总延迟与当前最优路径相当或更短的新路径时，算法会增强这条路径上信息素的浓度，引导后续token更倾向于探索这条路径。同时，通过过程控制和结果反馈，算法可以逐步接近全局最优解。 文章定义了Token的数据结构，包括走过变迁的索引序列和实际延迟时间，以及一个计时函数F，它综合了Token经过所有变迁的总时间。此外，还定义了一种带有记忆性和面向对象的连续时间随机Petri网（MemorialObject-Oriented Stochastic Petri Net, MOSPN），其中库所和变迁都具有存储和处理信息的能力。 该研究为解决随机Petri网中的路径寻优问题提供了一种新的方法，该方法对时间延迟具有较高的灵敏度，并能准确选择路径。通过结合概率分析和蚁群算法，该方法在处理复杂的系统建模和优化问题时表现出了优势。