Journal of Applied Mathematics
available knowledge for analyzing and designing the NCSs.
In practice, this kind of information including the variation
of time delays and packet losses is hard to obtain. e
problems of partly unknown transition probabilities were
investigated [–]. Zhang et al. investigate the stability
of Markovian jump linear systems with partly unknown
transition probabilities [, ]. Wang et al. study the partially
mode-dependent
∞
ltering problem for discrete-time
Markovian jump systems with partly unknown transition
probabilities []. Sun and Qin investigate the stability and
stabilizationproblemsofaclassofNCSswithboundedpacket
dropout, in which the transition probabilities are partly
unknown due to the complexity of network []. However,
the developed controllers of these references [–]onlyare
either mode independent or one-mode dependent, and the
design problem can thus be readily converted into a standard
MJLS problem. To the best of the authors’ knowledge, if
the transition probabilities are assumed partly accessible,
designing the two-mode-dependent controller that simulta-
neously depends on both the current S-C delay (
𝑠𝑐
𝑘
), and
themostrecentavailablesamplingperiod(
𝑘−𝜏
𝑠𝑐
𝑘
)hasnot
been fully investigated, which is the focus of this work.
When considering both
𝑠𝑐
𝑘
and
𝑘−𝜏
𝑠𝑐
𝑘
,theresultingclosed-
loop system can be transformed to a special MJLS, and thus
the well-developed results on MJLSs with partly unknown
transition probabilities cannot be directly applied [–].
In this paper, the stochastic stability of NCSs with random
time delays and random sampling periods is studied, in which
time delays and sampling periods are driven by two nite-
state Markov chains. is paper is organized as follows. In
Section , the NCSs model with random S-C time delays
and random sampling periods is made, which is equivalent
to a class of special discrete-time jump linear systems with
two modes. Sucient and necessary conditions of stochastic
stability with completely known transition probabilities for
the foregoing model are considered in Section .Sucient
conditions of stochastic stability with partly unknown tran-
sition probabilities for the foregoing model are considered in
Section . Section is an illustrative example, and our work
in this paper is summarized in Section .
Notation. In this paper, R is the set of all real numbers, R
𝑛
denotes the -dimensional Euclidean space. (,,)denotes
the probability space. A
𝑇
and A
−1
denote the transpose and
the inverse of a matrix A,respectively.A >0 (A <0)means
that A is positive denite (negative denite). 0 and I are
the zero and identity matrices with appropriate dimensions,
respectively. In symmetric block matrices, we use an asterisk
(∗)to represent a term that is induced by symmetry.
2. Problem Formulation
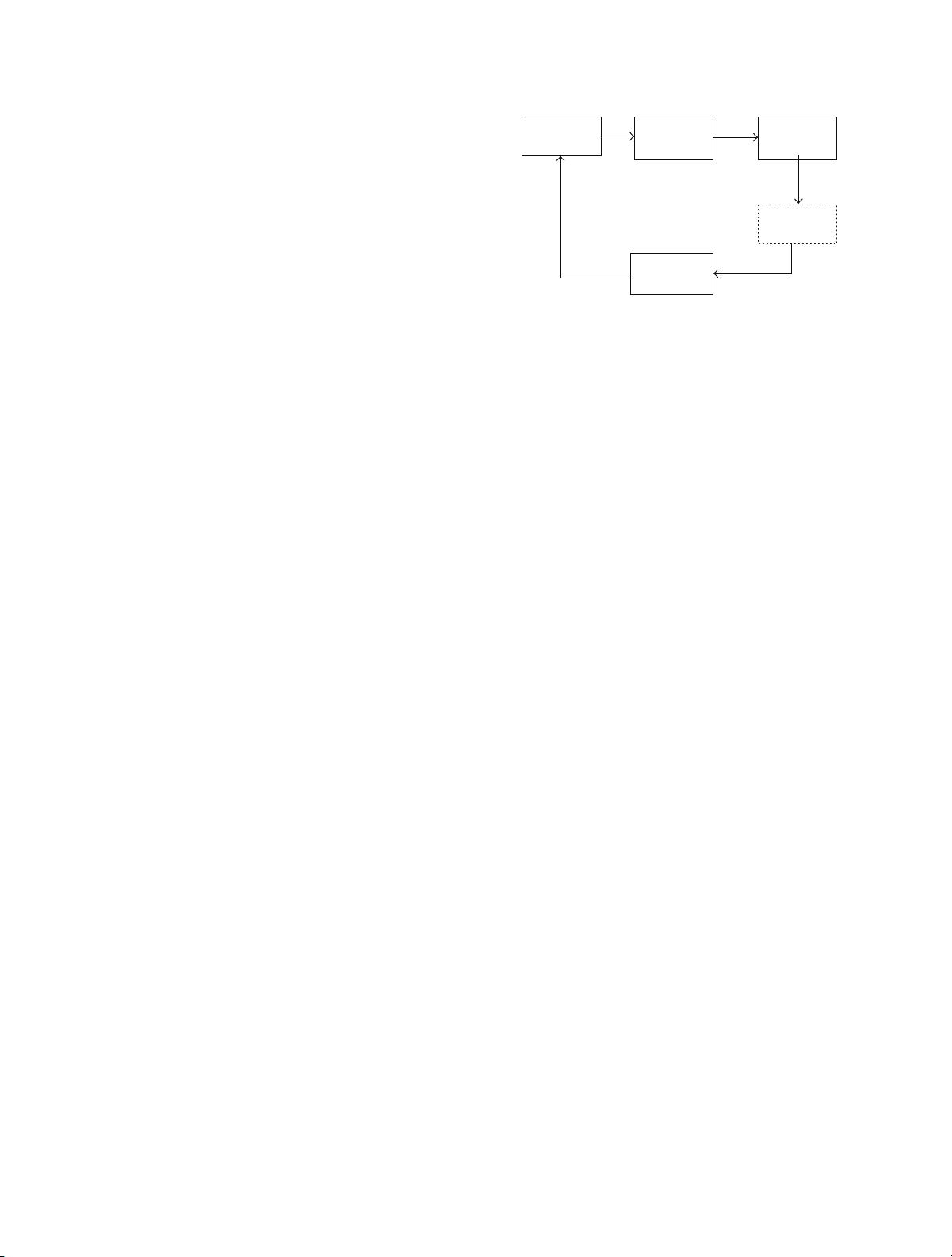
e structure of the considered NCSs is shown in Figure ,
where the plant is described by the following linear system
model:
(
)
=
(
)
+
(
)
,
()
where x(t)∈R
𝑛
,()∈R
𝑚
are the system state vector and
control input vector, respectively; ,are known constant
PlantActuator Sensor
Controller
Network
∼x
k
x
k
u
k
F : Diagram of NCSs.
matrices of appropriate dimensions. Suppose the sensor
is clock-driven, the controller and the actuator are event-
driven.
Suppose bounded random delays only exist in the link
from sensor to controller, as shown in Figure .Here,0≤
𝑠𝑐
𝑘
≤
𝑠𝑐
represents the S-C delay. e state feedback
controller is to be designed.
For NCSs, the shorter the sampling period, the better
system performance; however, the short sampling period will
increase the possibility of network congestion. If the constant
sampling period is adopted, the sampling period should
be large enough to avoid network congestion, so network
bandwidth cannot be suciently used when the network is
idle. In [–], the variable sampling method is used, and the
samplingperiodsareassumedtoswitchinanitediscrete
set. But when the systems switch too fast, it is apt to cause
oscillation and instability of the system. In the actual network,
the size of sampling period is closely related to the network
load. However, the network load usually is random []. As a
result of the above, network load can be high load, low load,
and medium load. Correspondingly, sampling periods can
randomly switch between three cases of maximum, medium,
and minimum in this paper. In the following, we consider
that sample periods randomly switch between three cases and
make NCSs model with random time delays and random
sample periods. us, not only the network bandwidth can
be fully used, but also the conservativeness of the stabilization
conditions of NCSs can be reduced.
Suppose
𝑘
is the length of the kth sampling period,
if the network is idle, dene the sampling period as
max
,
and if the network is occupied by the most users, dene
the sampling period as
min
, otherwise dene the sampling
period as (1/2)(
max
+
min
).en,thesamplingperiod
𝑘
∈
{
min
,(1/2)(
max
+
min
),
max
}.
e discrete-time expression of the system ()isas
follows:
(
+1
)
=Φ
𝑘
(
)
+Γ
𝑘
(
)
,
()
where Φ(
𝑘
)=
𝐴ℎ
𝑘
,and Γ(
𝑘
)=∫
ℎ
𝑘
0
𝐴𝑡
.
In this paper,
𝑠𝑐
𝑘
and
𝑘
are modeled as two homoge-
neous Markov chains dened in (,,)that take values in
= {0,1,...,
𝑠𝑐
}and ={1,2,3}, and their transition




 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜 信息提交成功
信息提交成功

