没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论

Mean Shift 概述
Mean Shift 简介
Mean Shift 这个概念最早是由 Fukunaga 等人[1]于 1975 年在一篇关于概率密度梯度函
数的估计中提出来的,其最初含义正如其名,就是偏移的均值向量,在这里 Mean Shift 是一个
名词,它指代的是一个向量,但随着 Mean Shift 理论的发展,Mean Shift 的含义也发生了变化,如
果我们说 Mean Shift 算法,一般是指一个迭代的步骤,即先算出当前点的偏移均值,移动该点
到其偏移均值,然后以此为新的起始点,继续移动,直到满足一定的条件结束.
然而在以后的很长一段时间内 Mean Shift 并没有引起人们的注意,直到 20 年以后,也就
是 1995 年,另外一篇关于 Mean Shift 的重要文献[2]才发表.在这篇重要的文献中,Yizong
Cheng 对基本的 Mean Shift 算法在以下两个方面做了推广,首先 Yizong Cheng 定义了一族核
函数,使得随着样本与被偏移点的距离不同 ,其偏移量对均值偏移向量的贡献也不同,其次
Yizong Cheng 还设定了一个权重系数,使得不同的样本点重要性不一样,这大大扩大了 Mean
Shift 的适用范围.另外 Yizong Cheng 指出了 Mean Shift 可能应用的领域,并给出了具体的例
子.
Comaniciu 等人[3][4]把 Mean Shift 成功的运用的特征空间的分析,在图像平滑和图像分
割中 Mean Shift 都得到了很好的应用. Comaniciu 等在文章中证明了,Mean Shift 算法在满足
一定条件下,一定可以收敛到最近的一个概率密度函数的稳态点,因此 Mean Shift 算法可以用
来检测概率密度函数中存在的模态.
Comaniciu 等人[5]还把非刚体的跟踪问题近似为一个 Mean Shift 最优化问题,使得跟踪
可以实时的进行.
在后面的几节,本文将详细的说明 Mean Shift 的基本思想及其扩展,其背后的物理含义,
以及算法步骤,并给出理论证明.最后本文还将给出 Mean Shift 在聚类,图像平滑,图像分割,物
体实时跟踪这几个方面的具体应用.

Mean Shift 的基本思想及其扩展
基本 Mean Shift
给定 d 维空间 中的 n 个样本点
i
x
,i=1,…,n,在 点的 Mean Shift 向量的基本形式定义
为:
1
i h
h i
x S
M x x x
k
(1)
其中,
h
S
是一个半径为 h 的高维球区域,满足以下关系的 y 点的集合,
(2)
k 表示在这 n 个样本点 中,有 k 个点落入
h
S
区域中.
我们可以看到 是样本点 相对于点 的偏移向量,(1)式定义的 Mean Shift 向量
就是对落入区域
h
S
中的 k 个样本点相对于点 的偏移向量求和然后再平均.从直观
上看,如果样本点
i
x
从一个概率密度函数
f x
中采样得到,由于非零的概率密度梯度指向概
率密度增加最大的方向,因此从平均上来说,
h
S
区域内的样本点更多的落在沿着概率密度梯
度的方向.因此,对应的, Mean Shift 向量
( )
h
M x
应该指向概率密度梯度的方向
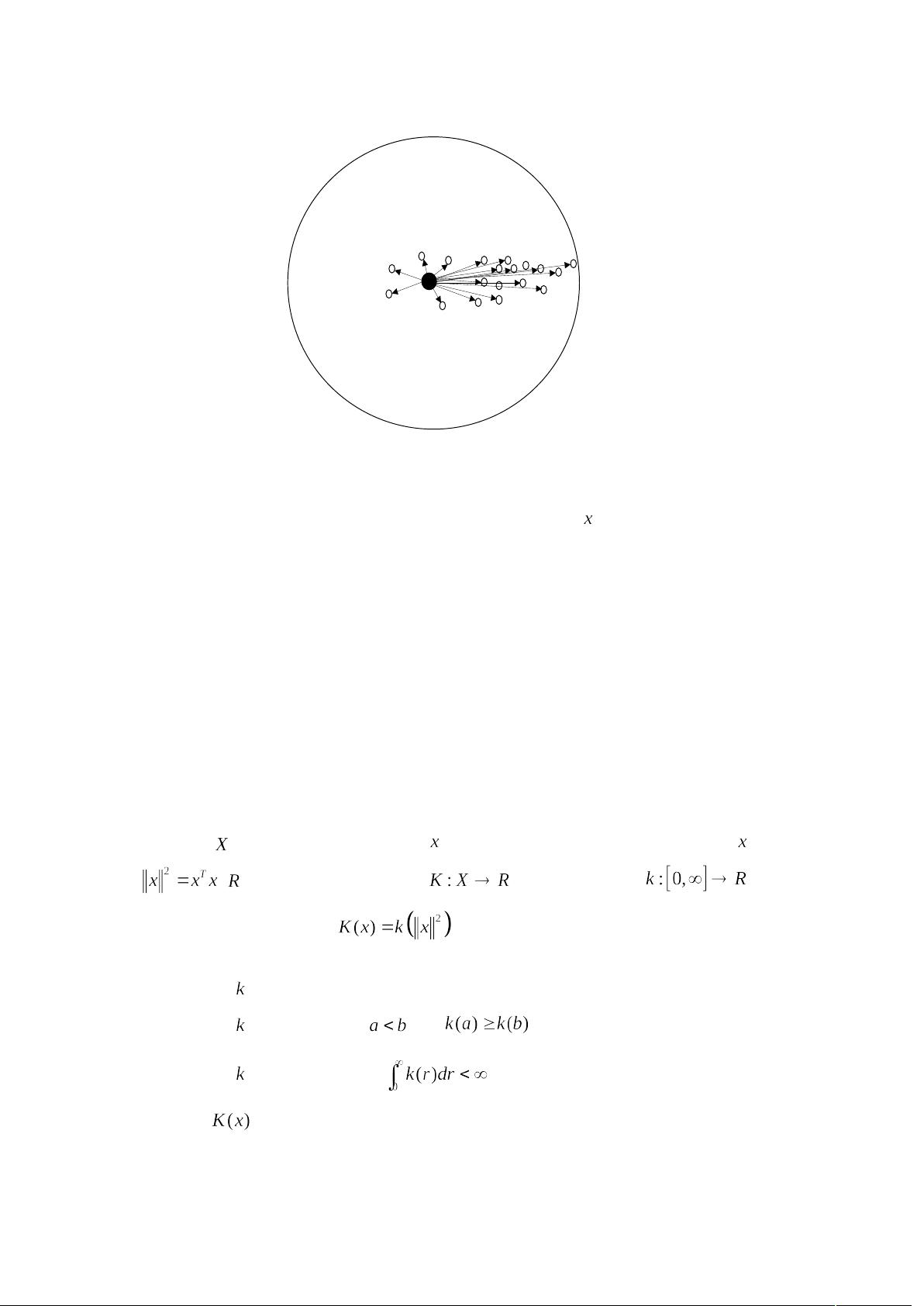
.
图 1,Mean Shift 示意图
如上图所示, 大圆圈所圈定的范围就是
h
S
,小圆圈代表落入
h
S
区域内的样本点
i h
x S
,
黑点就是 Mean Shift 的基准点
x
,箭头表示样本点相对于基准点 的偏移向量,很明显的,我们
可以看出,平均的偏移向量
( )
h
M x
会指向样本分布最多的区域,也就是概率密度函数的梯度
方向.
扩展的 Mean Shift
核函数
首先我们引进核函数的概念.
定义: 代表一个 d 维的欧氏空间, 是该空间中的一个点,用一列向量表示. 的模
. 表示实数域.如果一个函数 存在一个剖面函数 ,即
(3)
并且满足:
(1) 是非负的.
(2) 是非增的,即如果 那么 .
(3) 是分段连续的,并且
那么,函数 就被称为核函数.
举例:在 Mean Shift 中,有两类核函数经常用到,他们分别是,
剩余19页未读,继续阅读
资源评论

夜晚的星空90
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功