没有合适的资源?快使用搜索试试~ 我知道了~
The Scientist and Engineer's Guide to Digital Signal Processing ...
需积分: 3 1 下载量 72 浏览量
2009-10-01
23:52:12
上传
评论
收藏 341KB PDF 举报
温馨提示
Chapter 30 Complex Numbers.PDF
资源推荐
资源详情
资源评论

551
CHAPTER
30
h '
>
2
2
% vt
Complex Numbers
Complex numbers are an extension of the ordinary numbers used in everyday math. They have
the unique property of representing and manipulating two variables as a single quantity. This fits
very naturally with Fourier analysis, where the frequency domain is composed of two signals, the
real and the imaginary parts. Complex numbers shorten the equations used in DSP, and enable
techniques that are difficult or impossible with real numbers alone. For instance, the Fast Fourier
Transform is based on complex numbers. Unfortunately, complex techniques are very
mathematical, and it requires a great deal of study and practice to use them effectively. Many
scientists and engineers regard complex techniques as the dividing line between DSP as a tool,
and DSP as a career. In this chapter, we look at the mathematics of complex numbers, and
elementary ways of using them in science and engineering. The following three chapters discuss
important techniques based on complex numbers: the complex Fourier transform, the Laplace
transform, and the z-transform. These complex transforms are the heart of theoretical DSP. Get
ready, here comes the math!
The Complex Number System
To illustrate complex numbers, consider a child throwing a ball into the air.
For example, assume that the ball is thrown straight up, with an initial
velocity of 9.8 meters per second. One second after it leaves the child's
hand, the ball has reached a height of 4.9 meters, and the acceleration of
gravity (9.8 meters per second
2
) has reduced its velocity to zero. The ball
then accelerates toward the ground, being caught by the child two seconds
after it was thrown. From basic physics equations, the height of the ball at
any instant of time is given by:
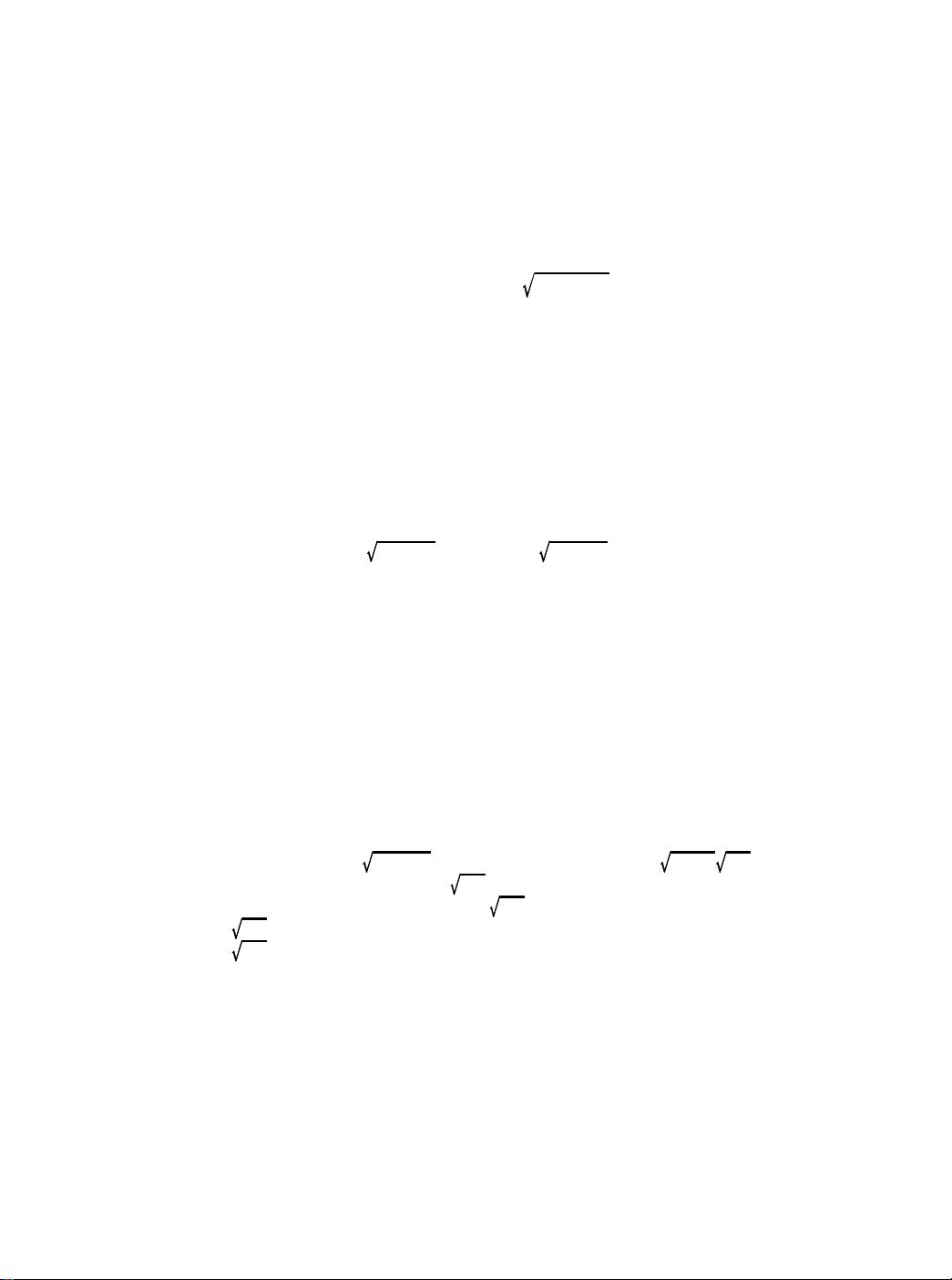
The Scientist and Engineer's Guide to Digital Signal Processing552
t ' 1± 1&h/4.9
where h is the height above the ground (in meters), g is the acceleration of
gravity (9.8 meters per second
2
), v is the initial velocity (9.8 meters per
second), and t is the time (in seconds).
Now, suppose we want to know when the ball passes a certain height.
Plugging in the known values and solving for t:
For instance, the ball is at a height of 3 meters twice: (going up)t ' 0.38
and seconds (going down). t ' 1.62
As long as we ask reasonable questions, these equations give reasonable
answers. But what happens when we ask unreasonable questions? For
example: At what time does the ball reach a height of 10 meters? This
question has no answer in reality because the ball never reaches this height.
Nevertheless, plugging the value of into the above equation gives twoh ' 10
answers: and . Both these answers containt ' 1% &1.041 t ' 1& &1.041
the square-root of a negative number, something that does not exist in the world
as we know it. This unusual property of polynomial equations was first used
by the Italian mathematician Girolamo Cardano (1501-1576). Two centuries
later, the great German mathematician Carl Friedrich Gauss (1777-1855)
coined the term complex numbers, and paved the way for the modern
understanding of the field.
Every complex number is the sum of two components: a real part and an
imaginary part. The real part is a real number, one of the ordinary
numbers we all learned in childhood. The imaginary part is an imaginary
number, that is, the square-root of a negative number. To keep things
standardized, the imaginary part is usually reduced to an ordinary number
multiplied by the square-root of negative one. As an example, the complex
number: , is first reduced to: , and then tot ' 1% &1.041 t ' 1% 1.041 &1
the final form: . The real part of this complex number is 1,t ' 1% 1.02 &1
while the imaginary part is . This notation allows the abstract term,1.02 &1
, to be given a special symbol. Mathematicians have long used i to denote
&1
. In comparison, electrical engineers use the symbol, j, because i is used&1
to represent electrical current. Both symbols are common in DSP. In this book
the electrical engineering convention, j, will be used.
For example, all the following are valid complex numbers: , ,1% 2j 1& 2j
, , , etc. All ordinary numbers, such as:&1% 2j 3.14159% 2.7183j (4/3)% (19/2)j
2, 6.34, and -1.414, can be viewed as a complex number with zero for the
imaginary part, i.e., , , and .2% 0j 6.34% 0j &1.414% 0j
Just as real numbers are described as having positions along a number line,
complex numbers are represented by locations in a two-dimensional display
called the complex plane. As shown in Fig. 30-1, the horizontal axis of the
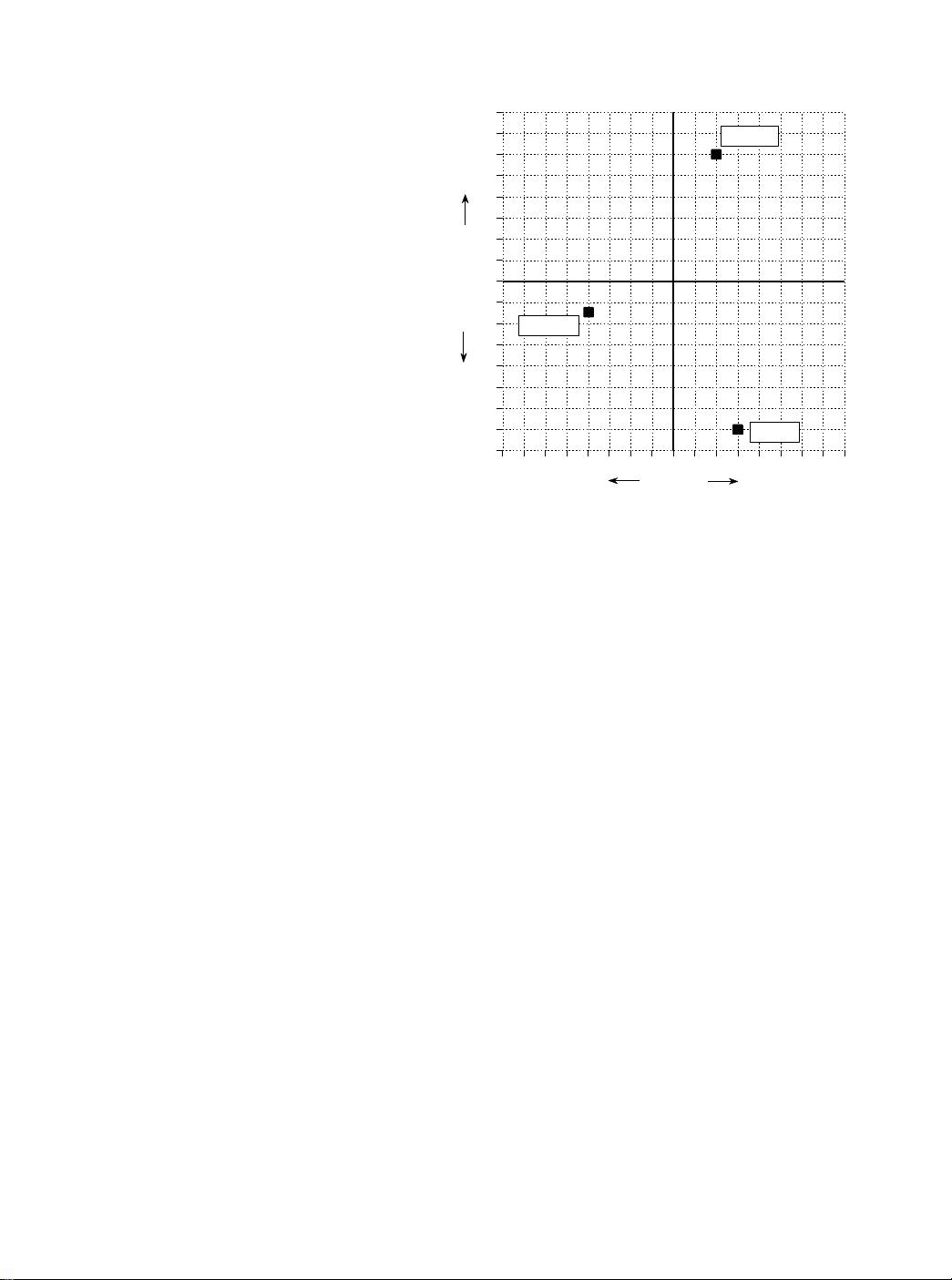
Chapter 30- Complex Numbers 553
Real axis
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8
2 + 6 j
-4 - 1.5 j
3 - 7 j
8j
7j
6j
5j
4j
3j
2j
1j
0j
-1j
-2j
-3j
-4j
-5j
-6j
-7j
-8j
FIGURE 30-1
The complex plane. Every complex number
has a unique location in the complex plane,
as illustrated by the three examples shown
here. The horizontal axis represents the real
part, while the vertical axis represents the
imaginary part.
Imaginary axis
A ' 2 % 6j
B ' &4 & 1.5j
C ' 3 & 7j
Re A = 2 Im A = 6
Re B = -4 Im B = -1.5
Re C = 3 Im C = -7
complex plane is the real part of the complex number, while the vertical axis
is the imaginary part. Since real numbers are those complex numbers that have
an imaginary part equal to zero, the real number line is the same as the x-axis
of the complex plane.
In mathematical equations, a complex number is represented by a single
variable, even though it is composed of two parts. For example, the three
complex variables in Fig. 30-1 could be written:
where A, B, & C are complex variables. This illustrates a strong advantage
and a strong disadvantage of using complex numbers. The advantage is the
inherent shorthand of representing two things by a single symbol. The dis-
advantage is having to remember which variables are complex and which
variables are ordinary numbers.
The mathematical notation for separating a complex number into its real and
imaginary parts uses the operators: and . For example, using theRe( ) Im( )
above complex numbers:
剩余15页未读,继续阅读
资源评论

thcx
- 粉丝: 1
- 资源: 54
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于ssm的家庭食谱管理系统-源代码(完整前后端+mysql+说明文档+LW).zip
- 基于ssm的汉服文化平台网站源代码(完整前后端+mysql+说明文档+LW).zip
- 613070841.docx
- 火焰烟雾训练参数yolov5s
- 火灾检测,视频推理结果
- Windows 11 环境下 条码阅读器输入到记事本的内容不完整
- 基于ssm的高校校园点餐系统源代码(完整前后端+mysql+说明文档+LW).zip
- 基于ssm的中国古诗词学习平台源代码(完整前后端+mysql+说明文档).zip
- 20241025_rpa培训.zip
- 基于ssm的新闻推送系统源代码(完整前后端+mysql+说明文档).zip
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功